«Параллель Тучкова». Часть четвертая, в которой появляются новые эксперты: Измеритель, Решатель и другие

Прежде чем мы с вами приступим к решению нашей задачи, я хочу описать те методы решения, которые нам в дальнейшем понадобятся. Однако еще до этого описания давайте вернемся на шаг назад и еще раз сформулируем, какую задачу (или задачи) мы решаем и каким (какими) способами. А потом уже определимся и с инструментами, которые будем использовать.

В самом общем виде проблему можно описать в виде задачи-минимум и задачи-максимум. Задачу-минимум можно сформулировать так: доказательно различить, используется ли для построения военно-топографической карты широта главной параллели в 52° или в 55°. Эта задача проще, поскольку предполагает выбор только из двух вариантов.

Задача-максимум же предполагает решение в более общем виде. Ее сформулируем так: найти универсальный метод определения широты главной параллели (путем неких измерений на картах) и оценить точность такого определения.

Какие расчетные способы мы с вами будем использовать для решения этих задач? Тут я не буду изобретать ничего нового: точно так же, как и во второй части повествования, будем измерять углы наклона касательной к параллели в точке пересечения ее с выбранным меридианом (относительно горизонтальной рамки карты) и сравнивать эти углы с расчетными значениями. Рассчитывать же эти значения будем по формуле из той же части, повторю ее еще раз немного в другом виде:

E = λ*cosφ/(ctgφ(1) + φ(1) - φ)  (2*)

где E – угол наклона, λ, φ – долгота и широта в измеряемой точке, φ(1) – наш оцениваемый параметр, то есть широта главной параллели [1].

Само построение также оставим прежним: угол наклона касательной к параллели для выбранного меридиана считаем равным углу наклона хорды, стягивающей два меридиана, соседних с выбранным. Напомню эту идею из второй части:

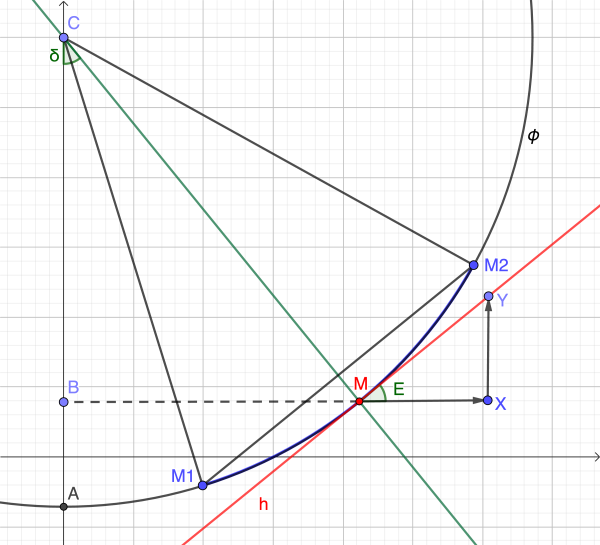
Таким образом, мы измеряем угол E путем измерения наклона хорды M1M2 к горизонтальной рамке карты. Измерив этот угол для различных значений широты и долготы, получим некоторое множество экспериментальных значений E, которые и будем сравнивать с рассчитанными по приведенной выше формуле.

Чтобы получить из этого сравнения значения параметра φ(1) снова воспользуемся на этом этапе хорошо известной процедурой – минимизацией суммы квадратов отклонений в каждой точке рассчитанных значений E от экспериментальных.

Давайте попробуем рассмотреть то, что мы хотим получить, на еще одном рисунке. Ниже построена трехмерная поверхность – график зависимости угла наклона E от широты φ и долготы λ [2]. Долгота на графике меняется от -12° до 12°, что соответствует примерному диапазону долгот военно-топографической карты, а широта для наглядности – от 0° до 80°. Анимация же графика отображает изменение величины параметра (широты главной параллели) от 40° до 80°. Также на график для примера нанесено несколько экспериментальных точек, измеренных на картах (о методике такого измерения – немного ниже). Видно, что наряду с изменением кривизны поверхности (это изменение я отметил в предыдущей части) вслед за изменением широты φ(1) изменяется также общий наклон поверхности и она то удаляется от экспериментальных точек (на краях диапазона φ(1)), то приближается к ним (где-то посередине этого диапазона).

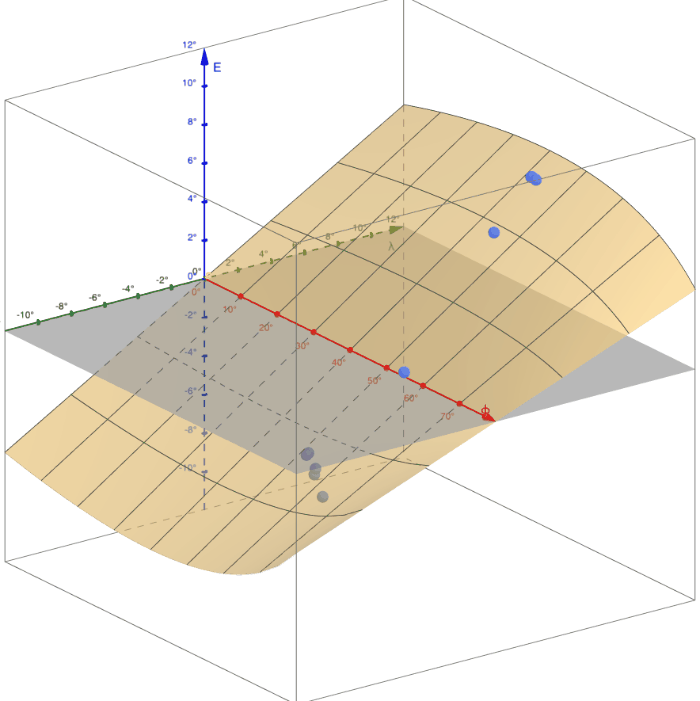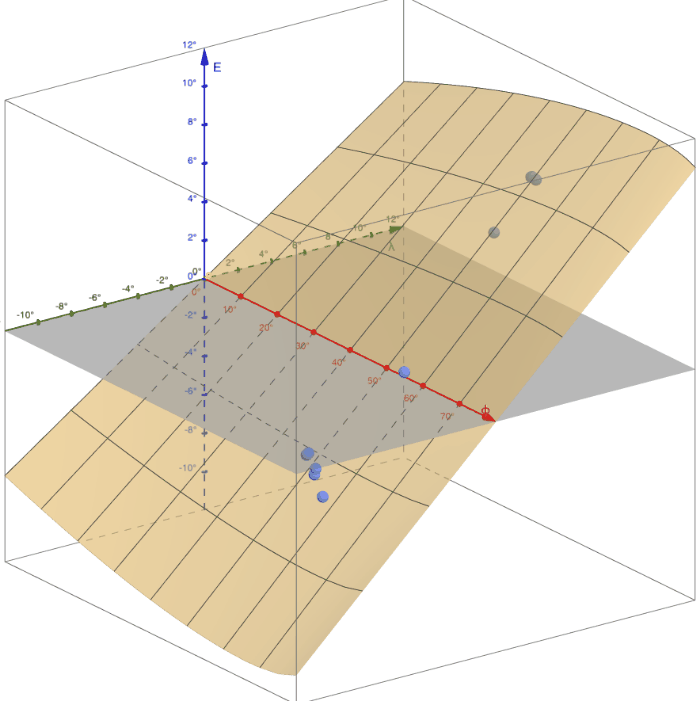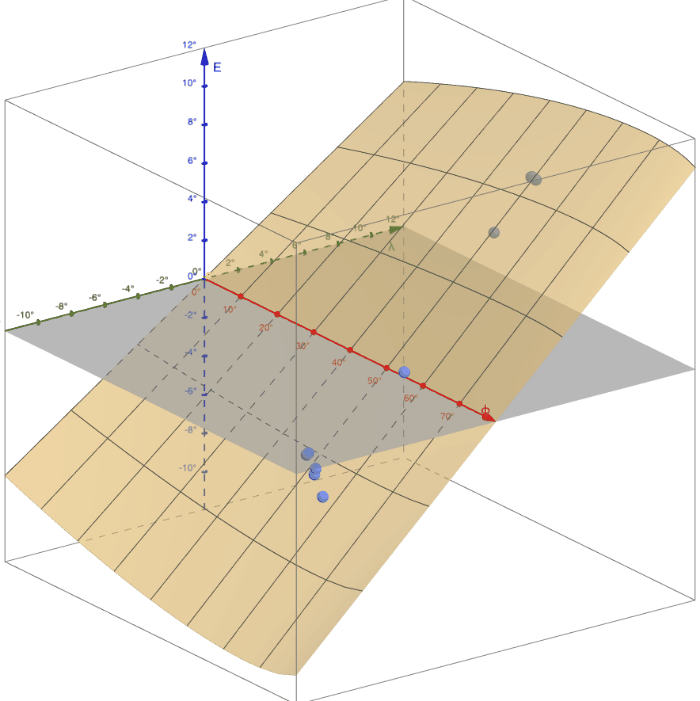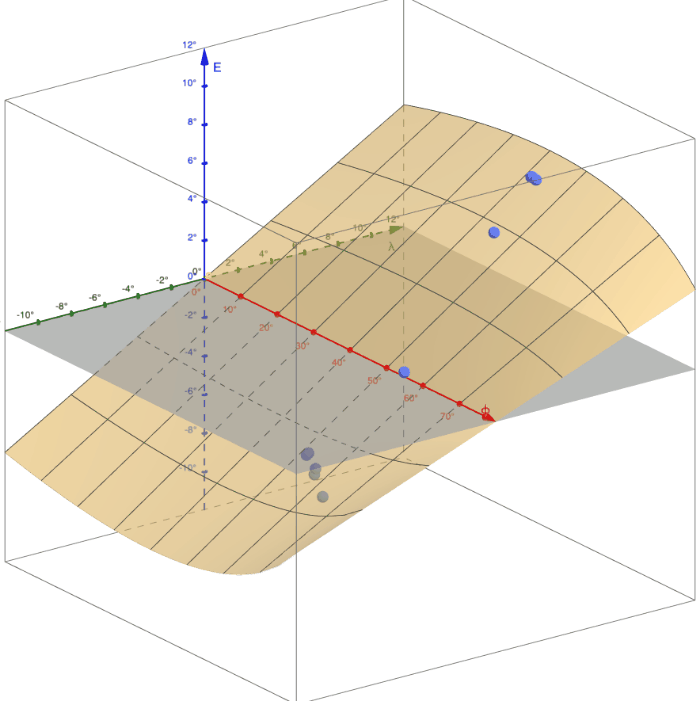
Нашей задачей и будет найти такое значение параметра φ(1), при котором это отклонение будет минимальным. А традиционный путь для этого – минимизировать сумму квадратов этих отклонений, чем на этом этапе мы скоро и займемся. А прямо сейчас давайте обсудим те новые инструменты для решения задачи, которые нам понадобятся.

Сделаю только еще одно важное замечание: все обсуждаемые ниже инструменты являются свободно распространяемыми (бесплатными) и кросс-платформенными (то есть их можно использовать в любой операционной системе). Я сознательно пошел на отказ от проприетарных и платных инструментов с тем, чтобы любой желающий мог повторить измерения и вычисления самостоятельно и в собственных целях [3].

Графический редактор GIMP и его Измеритель

Как помнит внимательный читатель, во второй части я указал на одно сомнение в исходных измерениях: программа Global Mapper, которой я когда-то пользовался, требует открытия измеряемого растра с присвоением ему некоторой «фиктивной» системы координат и проекции. Поэтому, чтобы в дальнейшем избежать подозрений в том, что программа может вносить искажения и деформации в исследуемый растр, мы с вами вообще откажемся от использования каких бы то ни было ГИС для измерений. Выход здесь давно известен: будем вести такие измерения в графическом редакторе, у которого есть специальные инструменты, предназначенные именно для этой работы. В частности, графический редактор GIMP, который я выбрал из-за его бесплатности и кросс-платформенности, имеет довольно удобный такой инструмент, который так и называется: «Измеритель» («Measure Tool»). Инструмент сразу же позволяет измерить не только расстояние между двумя точками в любых выбранных единицах длины, но и определяет угол наклона отрезка, проведенного между этими точками к горизонтальной границе растра.

Сама методика измерения угла совсем проста: вначале приблизительно соединяем инструментом интересующие нас точки:

А затем увеличиваем наш растр и поочередно перемещаем концы получившегося отрезка уже в точно отведенное для него место [4]:

После чего нам остается только считать значение угла наклона из окна Измерителя.

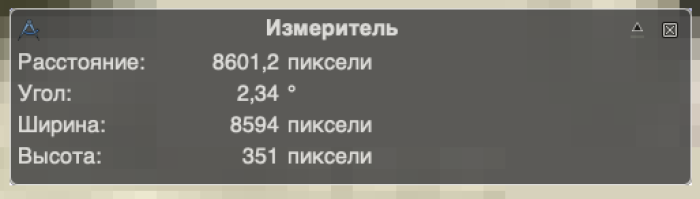
Сразу хочу обратить внимание, что измерение дает не только расстояние между точками (как гипотенузу получившегося прямоугольного треугольника) и угол, но и ширину с высотой – оставшиеся два катета. На самом деле, технически, инструмент измеряет именно «ширину» и «высоту» [5], а расстояние и угол получаются из простых внутренних тригонометрических вычислений. Таким образом, используя только лишь ширину и высоту можно рассчитать угол и самостоятельно, причем, казалось бы, с любой точностью. Однако в дальнейших расчетах я ограничусь лишь углом, рассчитанным самим редактором, а почему – будет сейчас понятно.

Для начала вспомним, что нам мало измерить угол наклона хорды между меридианами к горизонтальной границе растра. Этот угол нам еще необходимо исправить на величину угла наклона рамки карты относительно этой границы. Эта поправка необходимо возникает после сканирования листа карты из-за не точно горизонтального расположения листа при сканировании. Поправку нельзя не учитывать: мне попадались листы, «скошенные» относительно горизонтали более, чем на градус (впрочем, в большинстве случаев наклон составляет 0.5° и менее). Рассчитывать же я ее буду точно так же, как и во второй части: как среднее из измерений угла наклона для верхней и нижней горизонтальных сторон внутренней рамки карты.

Таким образом, каждое из измерений угла наклона на самом деле состоит из трех элементарных: угла наклона хорды к горизонтальной границе растра и двух измерений наклона рамки к этой границе [6]. В измерении же наклона рамки одна из измеренных величин (в пикселях), а именно – «высота», чаще всего выражается числом, имеющим одну или две значащие цифры (единицы или десятки пикселей). При этом и угол наклона, рассчитанный программой имеет величину в сотые или десятые доли градуса (две единицы после запятой). Вспоминая известные закономерности из теории ошибок измерений, можно заключить, что и суммарная точность из трех измерений не может быть лучше сотых долей градуса (а более строго – имеет величину в 0.02-0.03°). Таким образом очевидно, что точность в сотую долю градуса, посчитанную самим Измерителем, никаким расчетом до трех и более единиц после запятой нам улучшить не удастся и в этом смысле такие расчеты попросту не нужны [7].

Впрочем, это далеко не все. Как мы с вами увидим в дальнейшем, среднеквадратичное отклонение измеренных значений углов от расчетных составит примерно 5 минут (около 0.08°). Спрашивается, откуда берутся еще дополнительные 0.05-0.06° погрешности? Ответ довольно очевиден. Во-первых, это погрешности, допущенные при отрисовке, гравировке и печати самими составителями карты. А во-вторых (и мне эта причина представляется основной), неравномерной деформацией (старением) самих листов карты. Для справок реальные размеры листов также были измерены и я их приведу в следующей части. Если внимательный читатель их изучит, то сможет увидеть, что нет никакой заметной закономерности в отклонении размеров листов «по горизонтали» и «по вертикали». А если линейные размеры меняются не строго пропорционально, то это неминуемо влечет за собой искажения углов, первоначально верно изображенных на карте [8].

Подводя итог всем этим рассуждениям выше: простого «считывания» угла наклона, определяемого Измерителем, нам вполне будет достаточно, чтобы обеспечить с запасом необходимую точность измерений [9].

LibreOffice Calc и его Решатель

Теперь, когда мы с вами научились измерять нужные нам величины, их следует куда-то поместить, чтобы в дальнейшем обработать. Под «обработкой» следует понимать статистическую обработку, поскольку та численная задача, которую я обозначил в самом начале (минимизация суммы квадратов отклонений) является хорошо известной статистической задачей регрессии (в нашем случае – нелинейной). Кроме того, дальнейшая статистическая обработка позволит решить и другие, сопутствующие задачи, например, найти доверительный интервал значений получаемого в расчетах параметра. Тем не менее, слова «статистическая обработка» нас не должны пугать: для базовых возможностей такой обработки нам с вами не потребуется серьезный профессиональный программный пакет. Эти базовые возможности вполне обеспечит любой офисный процессор электронных таблиц. А по причинам, которые я обозначил выше (бесплатность и кросс-платформенность) мы с вами остановимся на пакете LibreOffice (преемнике OpenOffice) и входящему в этот пакет процессору таблиц Calc. По своим возможностям Calc ничем не уступает проприетарному (и платному) Excel.

Подробную структуру таблицы для расчетов я опишу в следующей части, а здесь расскажу, каким инструментом мы с вами будем пользоваться. Он располагается в меню «Сервис» программы и называется «Решатель» («Solver») [10]. Процедура, используемая пакетом для поиска решения заключается в получении значения в какой-то целевой ячейке таблицы, удовлетворяющего каким-то условиям (минимум, максимум или конкретное значение), изменяя для этого какую-то другую ячейку или группу ячеек.

Прежде всего надо объяснить Решателю, что мы именно решаем. А как уже было не раз сказано, мы находим минимум суммы квадратов отклонений экспериментальных значений угла наклона от их теоретических значений, рассчитанных по формуле (2*). Эту сумму квадратов мы и указываем в поле «Целевая ячейка». На анимации выше мы видели, что отклонения, а следовательно и сумма их квадратов зависит от значения параметра – широты главной параллели. Эту величину (любое разумное стартовое значение) и укажем в поле «Изменяя ячейки». Алгоритм сам будет менять значение, добиваясь решения задачи в целевой ячейке. Кроме того, на эту же изменяемую ячейку наложим и разумные ограничения. Дело в том, что алгоритм не знает, что в формуле (2*) величина параметра φ(1) имеет вполне определенный «физический» смысл широты и будет пытаться подбирать значения φ(1) вплоть до «плюс-минус бесконечности», при этом может найти и решения, которые меньше минимального значения из разумного диапазона широт. Конечно же, такие решения нас с вами не интересуют.

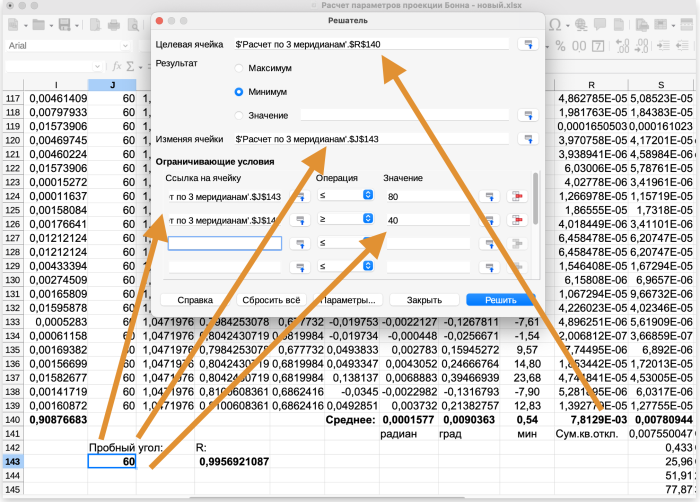
В настройках Решателя (кнопка «Параметры...» выберем нужный нам алгоритм решения. Calc предлагает для решения 4 варианта нелинейных методов (поскольку наша функция нелинейна, то линейные методы нас сейчас не интересуют). Первые два отдельных (DEPS evolutionary algorithm – алгоритм дифференциальной эволюции/роя частиц и SCO evolutionary algorithm – алгоритм социальной оптимизации) также использовать пока не будем: они требуют отдельной настройки многих параметров, в том числе тщательного подбора критериев сходимости. Используем «экспериментальный нелинейный решатель», который сам по себе состоит из таких же двух частей, что и упомянутый DEPS, но практически не требует настройки. Для расчетов будем использовать метод дифференциальной эволюции, который обеспечивает лучшую сходимость (подробнее этот момент мы с вами рассмотрим в следующей части). Установка алгоритма осуществляется нажатием кнопки «Правка» при выделенном соответствующем поле настроек и установки значения «0».

Установив все необходимые параметры, возвращаемся в главное окно Решателя. Нам остается только нажать кнопку «Решить».

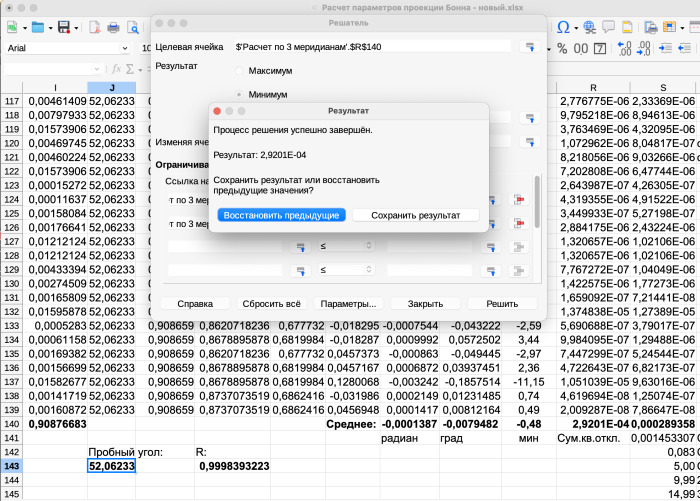
И через пару секунд в целевой ячейке появляется готовый результат – минимизированная сумма квадратов отклонений. Из рисунков видно, что алгоритм ее эффективно уменьшил примерно в 30 раз. А в ячейке пробного угла – и интересующее нас значение параметра, которое обеспечивает этот минимум суммы.

Подводя итог этого параграфа замечу, что внешний вид и настройки инструмента практически идентичны таковым в пакете Excel, а вот алгоритмы решений могут отличаться. Эти отличия мы с вами исследуем чуть позже. Что же касается расчета других вспомогательных статистических функций, которые находятся в меню «Данные – Статистика» и которые я буду использовать для расчета некоторых полезных вспомогательных данных, то они также идентичны «экселевским» и даже используют тот же синтаксис команд, что и Excel.

Необязательные (но полезные) инструменты

Двух инструментов, описанных выше, вполне достаточно для решения поставленной задачи. Однако я не могу не остановиться еще на двух полезных инструментах, которые я использую в первую очередь для хорошей визуализации исследуемых данных и полученных результатов в этих публикациях.

RStudio и язык R

Язык R – это специальный язык программирования, созданный для выполнения статистических и других научных расчетов, а RStudio – так называемая интегрированная среда разработки (IDE), позволяющая общаться с языком R средствами не только командной строки, но и в удобном графическом интерфейсе. Как и все прочее, что я описал в предыдущих параграфах, они кросс-платформенны и бесплатны. Помимо мощных статистических возможностей, на порядок или порядки превосходящие таковые в самых продвинутых офисных пакетах, язык R содержит и инструменты визуализации (построения статистических графиков, например, гистограмм). Ниже для примера приведу гистограмму распределения отклонений рассчитанных значений угла от экспериментальных после выполнения процедуры, описанной в предыдущем параграфе (на гистограмме для наглядности величины остатков пересчитаны из радианов в минуты).

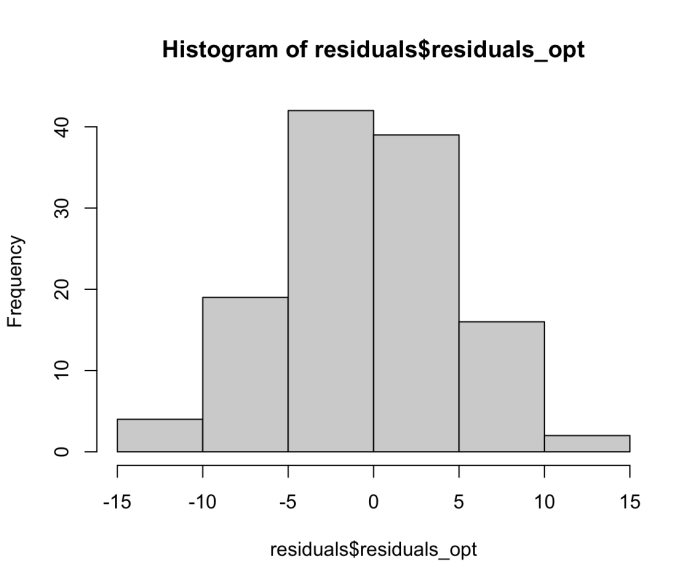
Такая гистограмма с заботливо подобранным самой функцией пакета оптимальными интервалами (в отличие от любых электронных таблиц) строится в RStudio буквально в несколько кликов мышью.

Между прочим, для тех, кому при чтении этого цикла не хватает каких-то основных знаний из области статистики, существует прекрасная книжка австралийского автора Даниэль Наварро [11]. В книге простым и понятным языком изложены базовые понятия статистики и статистической обработки данных и на сегодняшний день лично я считаю ее лучшим учебником по основам статистики.

Geogebra Classic 6

Многие графики функций, непосредственно не связанные со статистикой, в этом цикле построены с помощью математической программы Geogebra, в том числе и анимация в самом начале этой части. Можно было бы в очередной раз и не упоминать о бесплатности и кросс-платформенности программы, которая в дополнение к базовым Windows, Mac OS и Linux-версиям имеет даже дистрибутивы под мобильные устройства и онлайн-версию.  Скажу только, что возможности программы не ограничиваются красивым построением графиков, часто с ее помощью удобно искать решения сложных уравнений графическим методом, а также находить особые точки (например, экстремумы) сложных функций без необходимости их дифференцирования. В частности, некоторые свои выкладки я проверял именно таким способом.

Литература и примечания.

1. Напомню, что формула справедлива для сферы, а не для эллипсоида, и для угловых величин в радианах. Сфера имеет только один параметр R,  поэтому при записи в таком виде он сокращается.

2. В третьей части я ограничился двумерным графиком зависимости E от широты при разных значениях долгот и широты главной параллели.

3. Впрочем, полностью от проприетарных пакетов я не отказываюсь. Однако везде в этом цикле буду использовать их лишь для сравнения и проверки работы основных инструментов.

4. Если мы измеряем угол наклона хорды, стараемся поместить концы инструмента в середины линий пересекающихся параллели и меридиана, как это показано на рисунке. Если же мы измеряем линии внутренней рамки, о чем дальше по тексту, разумным кажется помещать концы инструмента не на середины линий, а на внутренние по отношению к самой карте края. Это связано с безобразно широкими этими линиями для листов карт поздних изданий (офсетная печать с фотокопий на плохой бумаге) по сравнению с ранними изданиями (печать с гравированных медных досок).

5. Причем в пикселях, а другие единицы длины получаются расчетным путем исходя из разрешения растра и выбранной единицы измерения.

6. Строго говоря, эти два последних измерения усредняются, что уменьшает погрешность измерения, однако для понимания качественной картины в дальнейших рассуждениях это не важно.

7. Тем не менее, в последующих таблицах я привожу и эти расчеты (с точностью до 3 знаков после запятой) – исключительно в целях поверки получившегося значения угла наклона.

8. Выявление закономерностей деформации листов карт в зависимости от времени, условий хранения и т.д. точно выходит за рамки наших с вами задач; будем считать эти отклонения случайными во вполне статистическом смысле. Однако, там есть еще одна «литературная» загадка, так что возможно позже я ее обсужу в отдельной статье.

9. Говоря о достоинствах инструмента Измеритель пакета GIMP, нельзя не упомянуть и о паре его недостатков. Первый – скорее не недостаток, а особенность: углы, которые он рассчитывает всегда получаются делением длины меньшего катета прямоугольного треугольника на больший. Из этого следует, что во-первых, углы лежат в диапазоне от 0° до 90°. Это нам никак не мешает, поскольку и расчетные углы лежат в этом диапазоне. Во-вторых, углы получаются всегда положительными – а вот здесь надо быть внимательным, поскольку наши расчетные формулы предполагают и наличие отрицательных углов. Поэтому для единообразия мы с вами всегда будем приписывать положительное значение угла для отклонения против часовой стрелки и отрицательное – для отклонения по часовой стрелке. Это следует непосредственно из приведенной формулы для угла E и связано со знаком долгот относительно центрального меридиана.

Второй недостаток, пожалуй, серьезнее. Как видно на приведенных рисунках, цвет линии инструмента – всегда светлый и нет никаких простых способов изменить стиль линии, не погружаясь в самые недра программы. Это хорошо для темного фона, но крайне тяжело для измерений на светлом фоне, а наши трехверстные карты, увы, именно таковы.

10. В английском интерфейсе это название полностью идентично аналогичному пакету Excel («Solver» – «Поиск решения»).

11. Danielle Navarro. Learning statistics with R: A tutorial for psychology students and other beginners. Если вас интересуют только начальные сведения по статистике, книгу можно читать примерно с середины, с 5 главы. А если вы начнете с самого начала, то заодно освоите и основы языка R.

Вы можете поблагодарить автора этой статьи, например, здесь.