«Шар наш земной — да что же он такое?» (окончание)
ДАВАЙТЕ ВЕРНЁМСЯ К СТАРЫМ КАРТАМ (продолжение)
В первой части нашей статьи мы с читателем пришли к довольно любопытному выводу: несмотря на то, что за полтора века уточнений размеров земного эллипсоида длина его окружности увеличилась на 8,5 километров, погрешность, вносимая этим изменением на лист карты крупного масштаба, имеет величину меньшую, нежели предельная точность масштаба карты. Говоря иными словами, неважно, эллипсоид какого размера вы будете использовать для создания карты или её привязки: это никак не скажется на точности построений.
На первый взгляд, это явно противоречит тому выводу, к которому мы пришли в одной из ранее опубликованных статей («Привязка архивных карт: некоторые секреты», № 1, 2015). Ведь там мы показали, что выбор эллипсоида иного размера, нежели тот, который использовался при создании карты, приводит к явному несовпадению линий координатной сетки, изображённой на карте с сеткой реальной, современной.
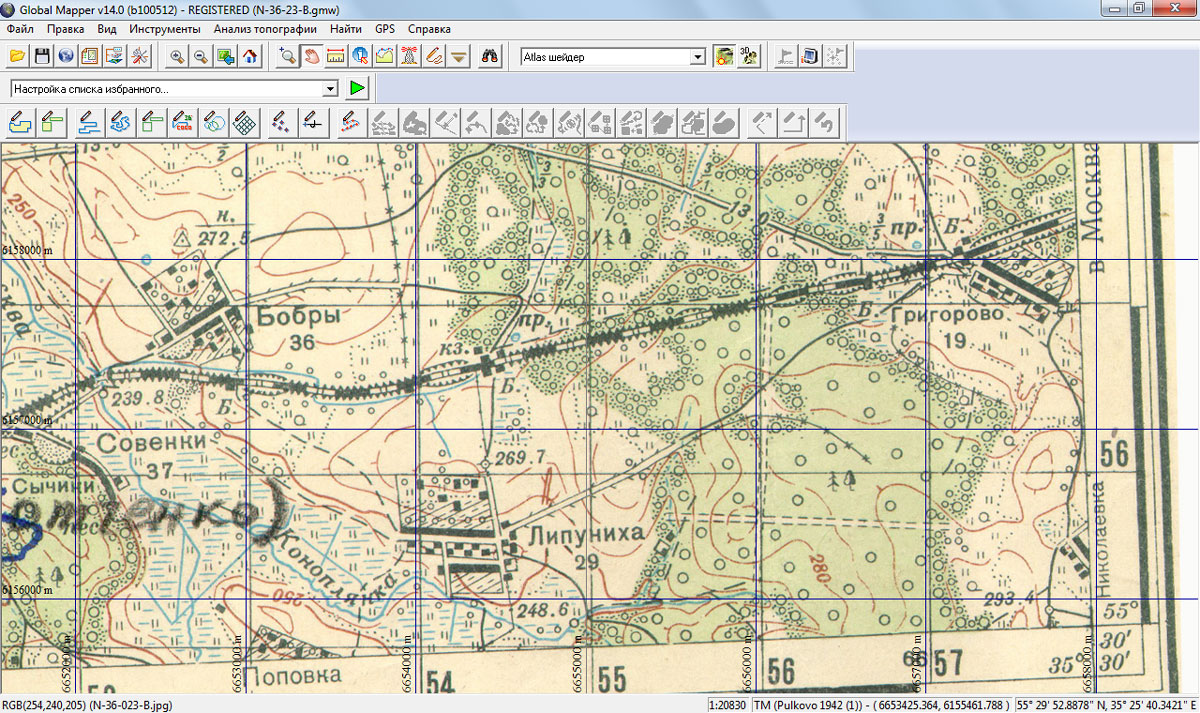
Несовпадение километровой сетки при выборе неправильного эллипсоида
Противоречие это кажущееся. Объясняется это двумя причинами, которые хочется разобрать немного подробнее.
Первое.
Из рисунка видно, что смещение карты происходит как по горизонтали, так и по вертикали. Но горизонтальное смещение намного меньше вертикального: в опубликованной статье я не стал заострять на этом внимание просто за недостатком места, да и не это было целью статьи; было важно показать сам принцип смещения. Так вот, такая разница объясняется тем, что километровая сетка в проекции Гаусса-Крюгера (а именно в этой проекции составлена карта примера) строится по вертикали от нулевой точки, которая находится на экваторе, а вот по горизонтали — от границы зоны, к которой принадлежит наша карта. Тем самым и получается совершенно разное расстояние «набегания погрешности» — от величины, примерно равной 1/8 дуги земной окружности до величины существенно меньшей.
Стоит подчеркнуть, что это объяснение относится только к смещению локальных координат (километровой сетки данной проекции). Географические же («градусные») координаты будут отличаться на разных эллипсоидах много меньше, но всё же будут, и это и будет второй причиной.
Второе.
В первой части статьи при обсуждении так называемых референц-эллипсоидов мы вкратце упомянули сдвиг и поворот этих эллипсоидов относительно общеземного. Именно таким способом для лучшего соответствия «подгоняют» эллипсоиды, подходящие для данной конкретной местности под общеземные. И, поскольку речь идёт не об изменении размера эллипсоида, а о физическом (хотя и умозрительном) сдвиге, то и географические координаты точек на эллипсоиде — референц- и общеземном — будут различаться. Вот такое различие, выраженное в единицах длины для разных референц-эллипсоидов может находиться в диапазоне от десятков до сотен метров. А математическое описание такого сдвига и определяет понятие так называемой системы координат (или, в англоязычной литературе — датума). Давайте теперь рассмотрим, как образуется система координат немного подробнее.
ПРО СИСТЕМЫ КООРДИНАТ
Наиболее полным описанием перевода одной системы координат в другую был бы полный учёт всех параметров, которые мы упоминали раньше: изменения размеров (и пропорций эллипсоида), сдвиг его в пространстве относительно общеземного и даже поворот его осей.
Наилучшим образом это можно представить следующим рисунком:
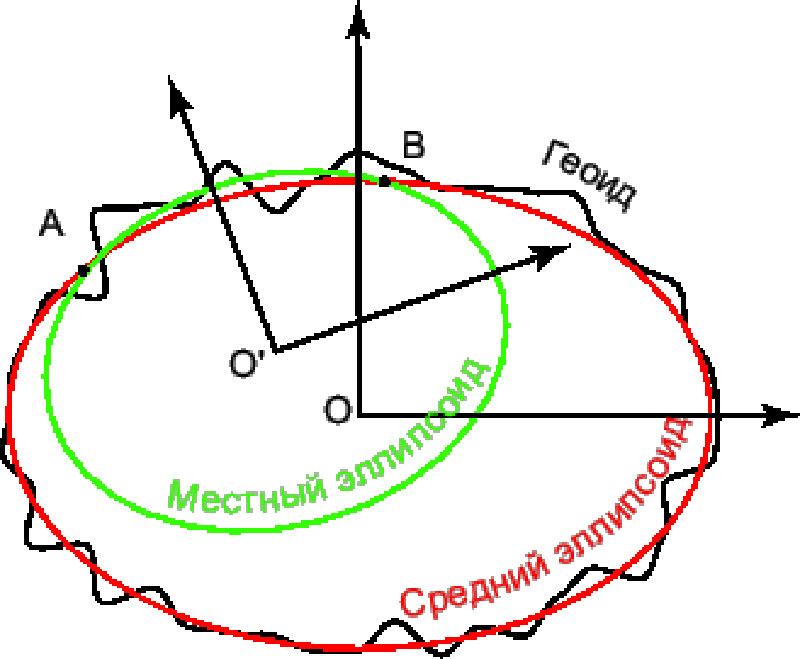
Сдвиг и поворот эллипсоида
«Средний» эллипсоид на нём — тот, который правильнее называть «общеземным», а «местный» — в этой статье мы называем «референц-эллипсоидом».
На практике, в численном виде, пересчёт координат происходит следующим образом: вначале географические координаты (широта, долгота и высота) пересчитываются в геодезические, в трёхмерной декартовой системе координат (при этом как раз и учитываются размеры эллипсоида), затем производят преобразование одним из способов, о которых подробнее — немного ниже, при этом также получают геодезические пространственные координаты и переводят снова в географические, но уже с учётом размеров нового эллипсоида.
Такие преобразования называют «прямыми», для них нужно знать параметры этих преобразований (те самые величины сдвигов и поворотов). Для того же, чтобы определить эти параметры, используют так называемые обратные преобразования — когда по имеющимся координатам (географическим или геодезическим) в двух разных системах координат их и определяют, как правило, численными методами.
Следует хорошо представлять себе такое обстоятельство: наибольший вклад в преобразования систем координат вносят три параметра сдвига, а вот повороты осей эллипсоида вносят вклад существенно меньший. Поэтому часто ограничиваются лишь учётом параметров сдвига. Такое преобразование называется трёхпараметрическим, или по фамилии учёного, впервые предложившего формулы для вычислений, преобразованием Молоденского. На самом деле, известны целых две разновидности этого преобразования — полное и упрощённое, в котором не учитывается изменение высоты каждой точки.
Если же мы хотим большей точности (а также того, чтобы наше преобразование подходило для обширной территории), то нам придётся учесть и повороты осей. На практике, добавляют ещё один параметр — масштабирование, то есть некоторый коэффициент, влияющий на абсолютную величину координат (его вклад в общую величину изменения координат также много меньше вклада сдвигов). Итого получаем уже 7 параметров, поэтому такое преобразование называют семипараметрическим, или по имени его создателя преобразованием Хелмерта. Тут тоже известно, как минимум, три вариации такого преобразования, два из которых называются преобразованиями Бурса-Вольфа, но чтобы окончательно не запутать читателя, скажу, что всё их различие — в знаках, которые приписываются к абсолютной величине каждого параметра.
Итак, системой координат с практической точки зрения следует назвать набор следующих параметров: величину большой и малой полуосей эллипсоида (или, что то же самое, одну из полуосей и величину сжатия), три параметра сдвига эллипсоида относительно выбранного общеземного и, если необходимо, ещё три параметра поворота осей и параметр масштабирования.
Нужно иметь в виду ещё и один факт: если бы для подгонки референц-эллипсоида под общеземной нам не нужно было бы его «двигать и вертеть», то и о размерах этого эллипсоида нам не нужно было бы беспокоиться: все географические координаты одного однозначно бы отобразились на географические координаты другого. Различие из-за изменения размеров было бы только в так называемых локальных координатах, каковыми, к примеру, является километровая сетка проекции Гаусса-Крюгера. Но, из-за того, что размеры эллипсоидов входят в явном виде в формулы пересчёта географических координат в декартовы, геодезические, то сдвигая тем или иным способом эллипсоид в пространстве, мы вынуждены эти размеры учитывать.
«АРШИНОМ ОБЩИМ НЕ ИЗМЕРИТЬ…»
Внимательный читатель, наверное, ещё при чтении первой части статьи, уже задал вопрос: а что это все размеры эллипсоидов приведены в метрах? ведь исторически размеры планеты Земля измерялись в каких угодно единицах длины, но метры стали окончательно использоваться чуть ли не с начала XX столетия? В самом деле, ведь в русскоязычной научной литературе XIX века размеры эллипсоидов приводятся, как правило, в саженях!
Тут стоит рассмотреть историю вопроса немного подробнее. Тем более, что это впрямую связано с тем вопросом, к которому мы постоянно обращаемся в этой, да и в других статьях: точности, которая приемлема для тех или иных операций при работе с архивными картами.
Итак, впервые метр, как эталон длины был определён, как я упомянул ранее, в 1791 году в виде одной сорокамиллионной доли длины окружности Парижского меридиана. Для этого необходимо было определить хотя бы часть длины этой дуги — и такая огромная работа действительно была проведена с использованием геодезических методов. Стоит заметить, что поскольку параметры земного эллипсоида в то время были известны с малой точностью (работы были закончены в 1804 году), то и длина первоначального метра оказалась немного (на 0,2 мм) короче настоящей сорокамиллионной доли.
Но вот в чём дело: когда велись измерения, эталон метра ещё только предстояло создать! В самом деле, мы определяем метр, как некую часть меридиана, для этого нам нужно знать длину этого меридиана в некоторых независимых единицах. Поэтому измерения велись, конечно же, не в метрах. Для Франции единицей длины был туаз, и именно в туазах и был впервые измерен Парижский меридиан. (Не следует путать французские дюймы, которых в туазе 72, с английскими — это достаточно различные единицы длины).
Более того, железный эталон туаза был изготовлен ещё в 1735 году и с того времени широко использовался и в других измерениях Земли. Это следует подчеркнуть и запомнить: измерения в течение второй половины XVIII–начала XIX вв. велись с использованием точно определённого эталона длины.
Более того, имеется точно определённая связь между туазом и русской саженью. Так, ещё в 1816 году механиком Юрьевым была изготовлена «Железная сажень № 1» — линейка, на которую с одной стороны была нанесена сажень с разбивкой на дюймы, а с другой — было отмечено значение туаза. И в этом же году официально было установлено количество английских дюймов в сажени — 84.
В течение пары десятилетий в Российской империи было произведено ещё несколько эталонов как сажени, так и туаза, а в 1835 году «Основанием российской линейной меры оставить навсегда сажень в 7 настоящих английских футов с разделением на 3 аршина, каждый 28 дюймов или 16 вершков…» было установлено на уровне указа.
Таким образом, можно проследить полную преемственность и связь «на уровне железа» между туазами, в которых производились основные крупные геодезические измерения, и русскими саженями. Более того, из приведённого выше определения следует и однозначная связь с английскими дюймами.
А вот первый достаточно точный эталон метра (платиновый) был изготовлен только в 1799 году, да и в последующие годы его приходилось исправлять и уточнять, вплоть до 1889 года, когда был создан очередной вариант эталона из сплава платины и иридия.

Платино-иридиевый эталон метра, 1889 г.
Теперь можно сделать окончательный вывод: использование саженей для целей геодезии и картографии обеспечивало всю необходимую точность измерений. А переход на метрическую систему, что видно из табличек, приведённых ранее, стал возможным лишь после того, как были получены эталоны метра с необходимой точностью.
В заключение любопытно было бы остановиться на одном интересном расчёте. Выше уже была обозначена связь сажени и английского дюйма: в одной сажени 84 дюйма. С одной стороны, это даёт взаимно однозначное соответствие вершков, аршинов, саженей и вёрст с дюймами, футами и милями. С другой стороны, в литературе приводятся данные, говорящие о том, что связь дюймы-метры менялась с течением времени (понятно, что это было связано, в первую очередь, именно с уточнением физического размера метра). Я не буду приводить здесь всю хронологию изменений, возьму лишь крайние по датам данные: 1816 г. — 1 дюйм равен 2,5400438 см, 1947 г. — 2,5399931 см. На один дюйм получается разница в 0,00005 см, а в пересчёте на всю окружность Земли примерно 800 метров (или примерно 130 метров для одной из полуосей). Поэтому вполне разумным будет считать длину дюйма равной в точности 2,54 см (что и было окончательно принято в 1958 году), и это даёт для сажени окончательную и абсолютно точную для применений того времени (да и сегодняшнего!) величину в 2,1336 метра.
И ещё сказанное свидетельствует о том, что «аршин», упомянутый в заголовке, вплоть до перехода на метрическую систему был вполне общим.
Владимир Комиссаров