«Шар наш земной — да что же он такое?»

В предыдущих статьях этого цикла я подробно останавливался на том, какой необходимой информацией нужно обладать, чтобы грамотно обрабатывать архивные карты, в том числе для целей навигации на местности, а также для того, чтобы стало возможным соотнести информацию, изображённую на архивной карте с современным состоянием местности.

В последней статье я подробно разобрал тему желательности (и даже, порой, необходимости) знания проекции карты. Однако геодезическая основа упоминалась вскользь, как правило только для понимания основной мысли материала, хотя именно геодезия — краеугольный камень картографии. Теперь пришло время подробно поговорить и об этом. Давайте разберём, насколько важным для операций со старыми картами является это понимание и знание и в каких случаях этими сведениями можно пренебречь.

ПРО ЭЛЛИПСОИДЫ, ГЕОИДЫ И ПРОЧИЕ «ВЫСШИЕ СФЕРЫ» ГЕОДЕЗИИ

Основную задачу, стоящую перед картографом при построении географической карты, можно сформулировать так: отобразить с наименьшими искажениями на плоском листе бумаги подлинную картину местности, которая на самом деле располагается на земной поверхности. Я здесь сознательно хочу подчеркнуть самый сложный вариант задачи, отображение именно на плоский лист. Именно в таком виде географические карты начали своё существование; лишь сравнительно недавно, уже в компьютерную эру, появились возможности изображения местности сразу на трёхмерных поверхностях (хотя и остаётся задача изображения этих трёхмерных поверхностей на плоском экране монитора, но она решается уже несколько иными способами).

Задача отображения на плоский лист земной поверхности и решается с помощью разнообразных способов, именуемых «проекциями», о которых я подробно рассказывал в предыдущей статье. Однако, все эти способы разработаны (в том числе и в математическом, формульном виде) в одном предположении: поверхность Земли имеет форму сферы или эллипсоида. Только при таких условиях становится возможным численное, математическое решение задачи.

Тем не менее, сегодня мы знаем, что наша планета имеет гораздо более сложную форму: она не является даже эллипсоидом с разными размерами своих полуосей (трёхосным эллипсоидом), и уж тем более не является простой сферой. Как же быть в этом случае?

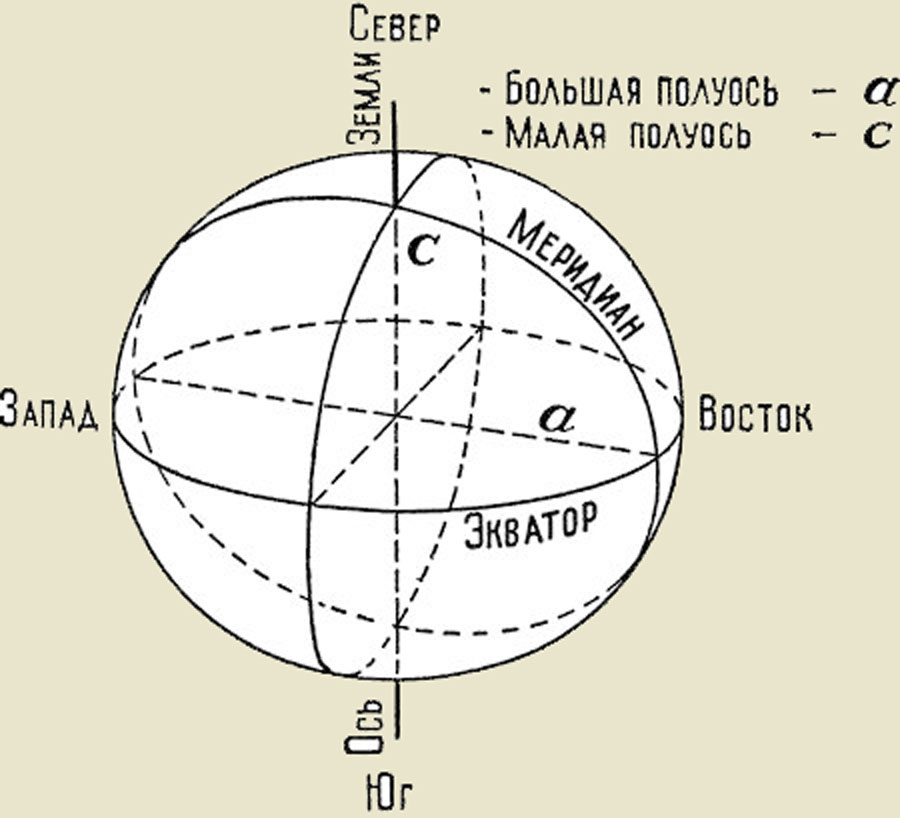
Земля как двухосный эллипсоид

Выше изображён простой двухосный эллипсоид, который также ещё называют эллипсоидом вращения. Именно эта модель и используется в картографии вплоть до нынешнего времени. Дело в том, что именно для неё возможны достаточно простые математические представления отображения её участков поверхности на ту или иную плоскость (именно об этом процессе и говорят, когда подразумевают ту или иную «проекцию»).

Как оно обычно бывает в жизни, реальная ситуация намного сложнее. На рисунке ниже изображён фрагмент поверхности так называемого «геоида», который (между прочим, тоже в приближении!) и описывает реальную земную поверхность.

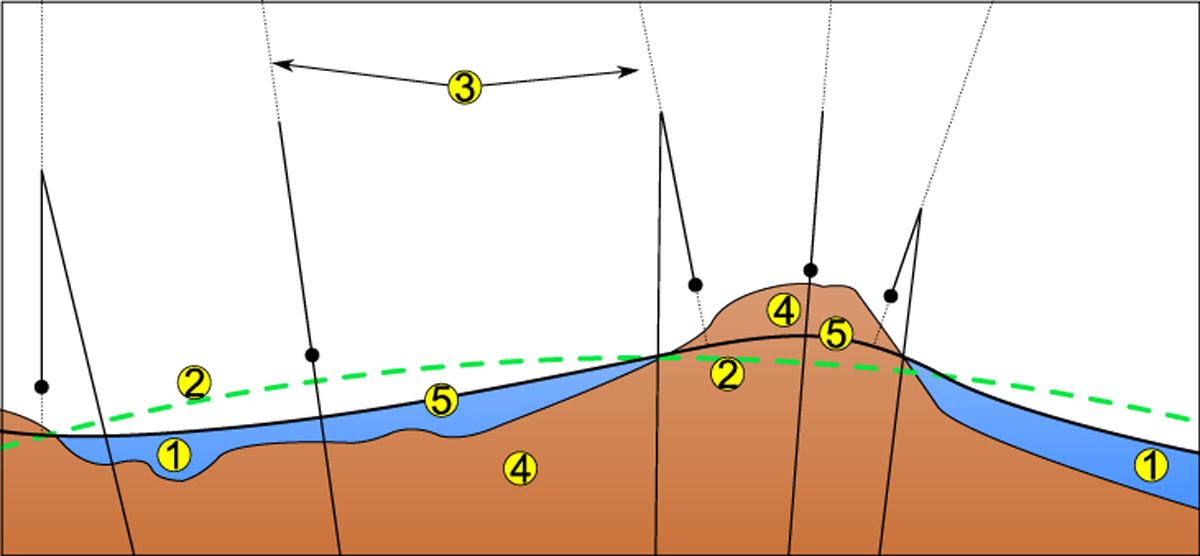
Поверхность геоида. Цифрами обозначены: 1 - мировой океан, 2 - земной эллипсоид, 3 - отвесные линии, 4 - тело Земли, 5 - геоид

По своему определению, поверхность геоида — это поверхность, перпендикулярная к направлению силы тяжести (отвесной линии) в каждой своей точке. Из рисунка видно, что в основном эта поверхность совпадает с поверхностью мирового океана, однако с поверхностью суши она уже совпадает лишь в некотором приближении. Ещё в большем приближении она совпадает с поверхностью эллипсоида, которая на рисунке изображена зелёной пунктирной линией.

Теперь из рисунка уже становится понятным, что наша задача усложнилась: нам нужно не только найти наилучший способ отображения эллипсоида на плоскость, но и найти наилучший способ отображения земной поверхности на эллипсоид. Стоит, однако, заметить, что само понятие «наилучший», точно так же, как и в случае с проекциями, зависит от тех целей, которые мы перед собой ставим. В частности, такая задача, как мы увидим ниже, может быть решена разными способами, в зависимости от того, ведём ли мы речь о всей земной поверхности, или лишь о её части. И здесь тоже возможны варианты, в зависимости от величины этой части.

Для того, чтобы понимать, как развивалась научная мысль в этом направлении, стоит вернуться на много веков назад.

По крайней мере, Аристотель был полностью убеждён в шарообразности Земли. Однако, первая попытка измерения её размеров принадлежит Эратосфену Киренскому (ок. 276–194 до н. э.). Я здесь не буду подробно останавливаться на изящном и остроумном способе его решения задачи; любопытный читатель легко найдёт его в сети Интернет. Упомяну лишь, что сам способ является по сути дела астрономическим, связанным с определением высоты Солнца в разных географических точках. Такие же или другие астрономические способы являются базовыми для всех измерений такого рода. К сожалению, мы не знаем, насколько точно Эратосфен измерил диаметр: дело в том, что все вычисления он проводил в типичных единицах своего времени, «стадиях», а как соотносятся «стадии» Эратосфена с современными единицами расстояний неизвестно. Встречающиеся иногда попытки оценки точности его измерений часто по принципу порочного круга выводят на определение длины стадии через его же измерения диаметра Земли. Так что давайте здесь ограничимся лишь тем бесспорным утверждением, что окружность Земли у него получилась равной 250 000 стадий, а стадия, определённая таким способом равна примерно 160 современным метрам. К этой неоднозначности «стадии Эратосфена» мы ещё будем возвращаться не раз ниже в статье.

В качестве других примеров попыток определения диаметра Земли стоит, пожалуй, упомянуть здесь индийского астронома и математика Арьябхату (476–550 гг.). И снова, как и в примере Эратосфена, до нас дошёл результат его вычислений, данный в «йоджанах», то есть в ростах человека, увеличенных в 8000 раз. Но здесь, по крайней мере, мы можем уже провести некоторую грубую оценку точности. В самом деле, полагая рост человека равным 160 сантиметрам, мы имеем йоджану равной 12,8 км и тогда для окружности Земли получится величина в 12,8 * 3300 (число, полученное Арьябхатой), или 42 240 км: довольно точное соответствие современным данным. Конечно, это определение содержит всё ту же неоднозначность: в качестве эталона у нас используется неточная и непостоянная величина, а именно рост человека. Вопросы эталонов мы также обсудим немного позже.

Из последнего примера хорошо видно, что с достаточно приемлемой точностью (приемлемой для многих целей!) размеры Земли были известны уже в начале новой эры. На попытках улучшить результаты в средние века мы здесь останавливаться не будем: они не сильно изменили предшествующие впечатляющие результаты. Пожалуй, стоит лишь упомянуть о двух вещах. Первое — это то, что экспериментально была показана «сплюснутость» Земли у полюсов. Это находилось в прекрасном соответствии с предсказанием сэра Исаака Ньютона о том, что Земля должна быть больше растянута у экватора, чем у полюсов из-за центробежной силы, возникающей при её вращении. Второе — развитие методов триангуляции, то есть измерения любых, сколь угодно больших расстояний с помощью геометрических построений, основанных на разбивке определяемого расстояния на участки, которыми являются стороны треугольников. Я снова не буду подробно останавливаться здесь на этих методах, скажу лишь, что идея здесь в том, чтобы определять неизвестные расстояния не прямым измерением, а с помощью геометрии, заменяя измерение длины на измерение углов.

Дальнейшее продвижение в этом направлении, связанное уже с качественным скачком в точности измерений, относится уже к концу XVIII–началу XIX века. Именно в это время начался взрывной рост такого рода измерений. Кроме того, окончательно пришло понимание того, что Земля не сферична, причём не сферична достаточно сильно. Впечатляющая таблица, подводящая итог целого столетия таких измерений, приведена в учебнике В.В. Витковского «Практическая геодезия», изданном в самом начале XX века.

​

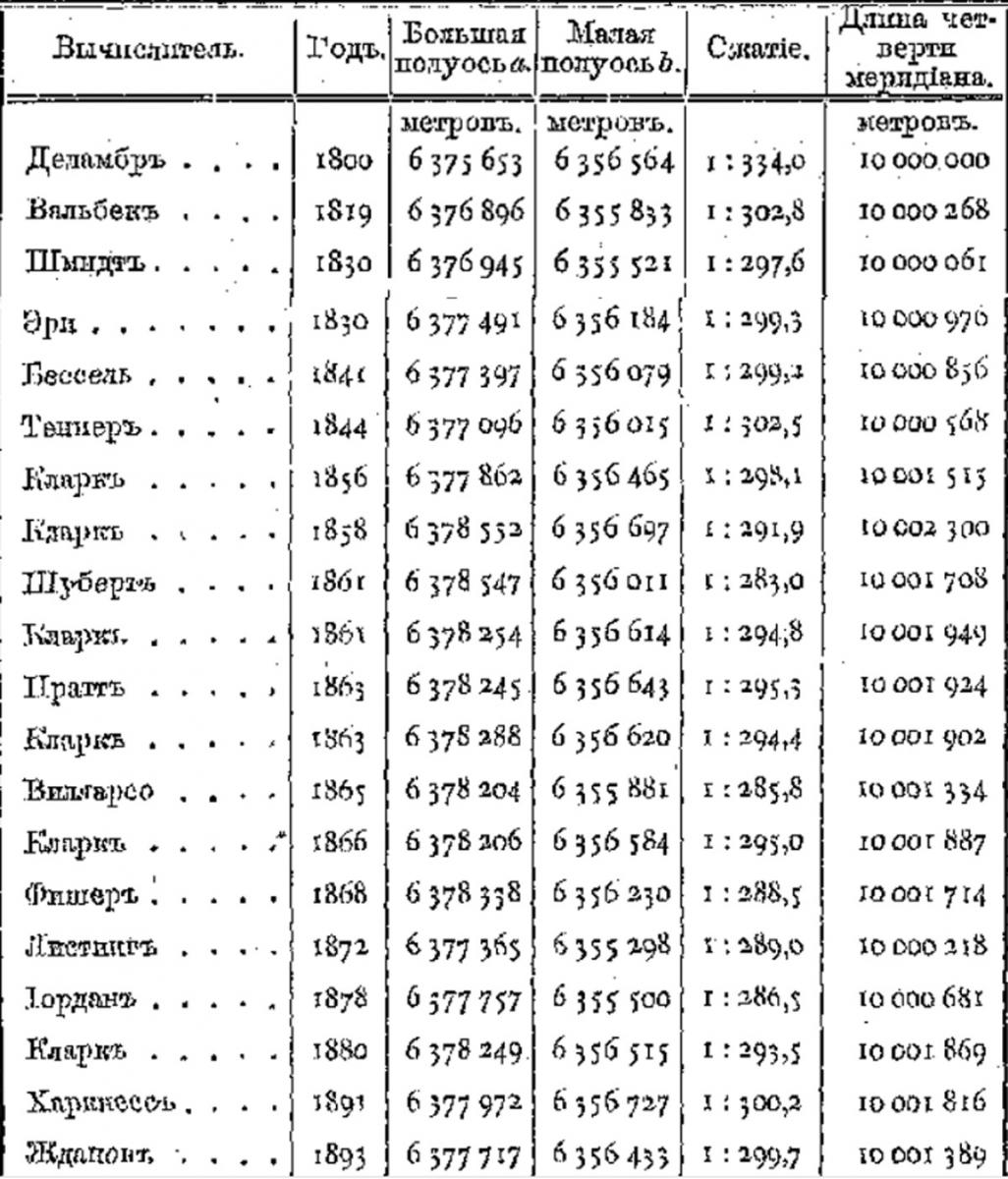
В этой табличке можно увидеть сразу несколько примечательных фактов, полезных для дальнейшего рассмотрения. Первое, что сразу же бросается в глаза — это то, что за неполное столетие большая полуось земного эллипсоида «выросла» на 2–2,5 километра! В длине окружности (точнее, эллипса, являющегося сечением земного эллипсоида) это увеличение выглядит ещё более впечатляющим: 12–15 километров. Много это или мало? На этот вопрос я постараюсь ответить чуть ниже.

Второе примечательное наблюдение — это вариации сжатия. Я снова не буду перегружать читателя лишними формулами, скажу лишь, что большая и малая полуоси эллипсоида и «сжатие» находятся во взаимно однозначном соответствии, а величина дроби варьирует в пределах нескольких процентов: именно в такой пропорции менялось представление о «сплюснутости» Земли у полюсов.

Наконец, третье наблюдение — это то, что в самой первой строчке, относящейся к измерениям Деламбра, длина четверти меридиана (в данном случае, речь идёт о Парижском меридиане), в точности равна 10 000 км. Это прямо связано с историей создания эталона метра, немного об этой истории я расскажу чуть позже.

Динамика изменений параметров земного эллипсоида становится более заметной, если посмотреть на сокращённый вариант таблицы, которая приведена в учебнике выдающегося учёного Ф.Н. Красовского «Руководство по высшей геодезии», вышедшем в 1926 году.

​

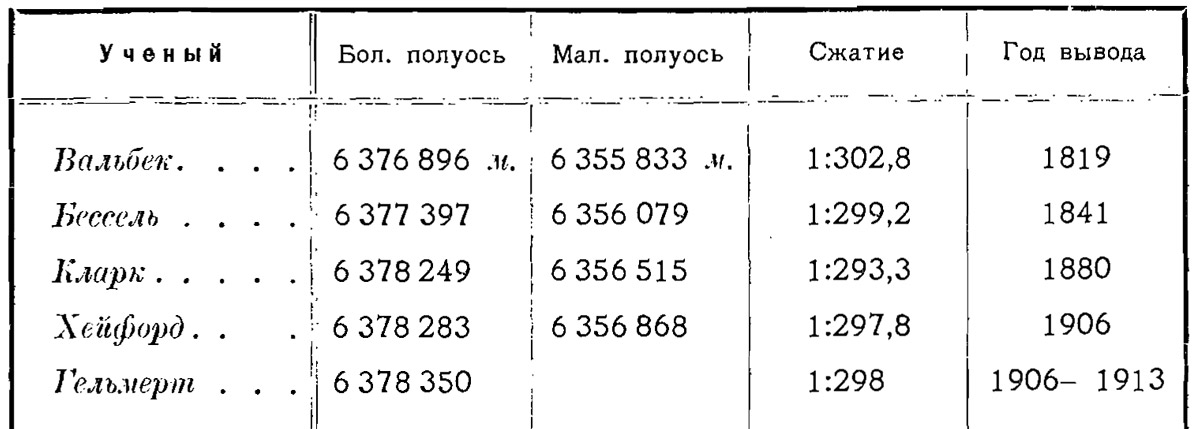
Таблица дополнена ещё двумя измерениями эллипсоида, относящимися к началу XX века. Но самая главная заслуга Ф.Н. Красовского в том, что именно им были предложены параметры ещё одного эллипсоида, который с успехом продолжает использоваться и в наши дни. Параметры эллипсоида его имени приведены в следующей таблице, взятой из популярного американского справочника 1987 года.

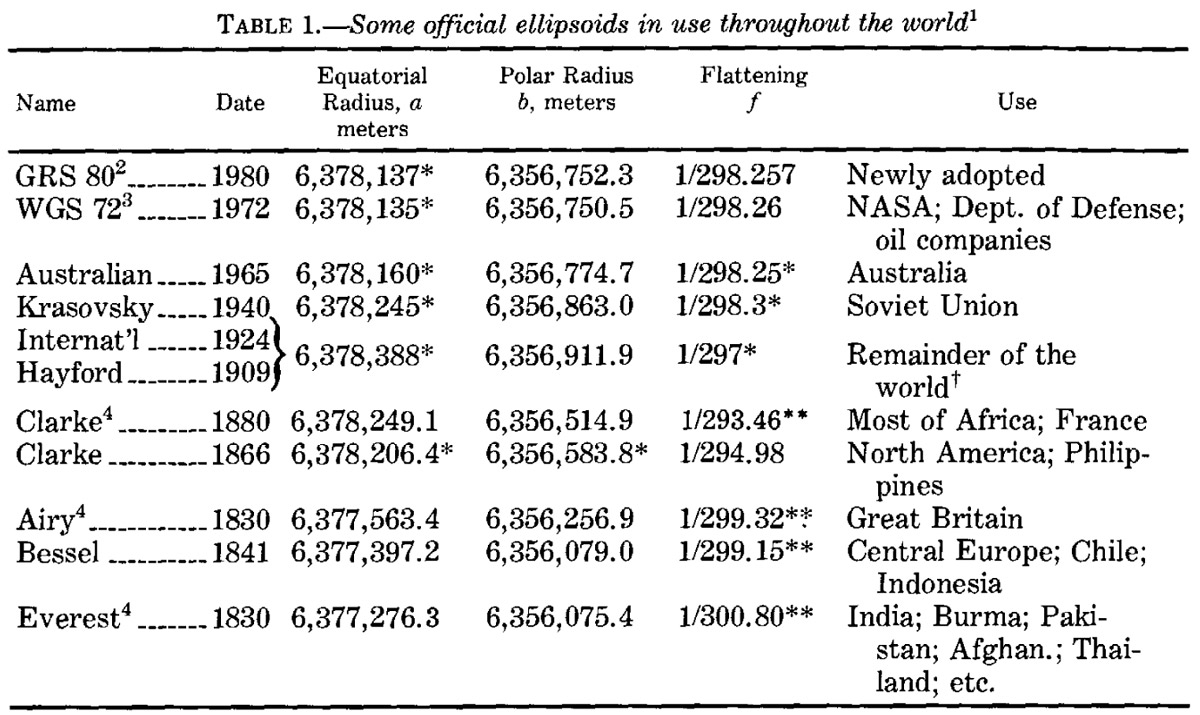
Из последней таблицы видно, что размеры полуосей эллипсоида начинают наконец-то сходиться к определённой величине, разница между последовательными данными становится уже меньше метра, да и параметр сжатия уже практически не меняется.

На этом месте я хочу прервать хронологический рассказ об изменениях в размерах эллипсоидов, потому что мы подошли к самой сути вопроса статьи: до какой степени точности нужно знать эти размеры и для чего это нужно?

КАКИЕ НУЖНЫ ЭЛЛИПСОИДЫ?

На самом деле, вопрос заданный в такой формулировке является довольно бессмысленным и самым правильным ответом на него будет встречный вопрос: «Для чего?»

Обратим своё внимание на последнюю табличку. В ней особняком стоят два самых поздних эллипсоида: WGS72 и GRS80. Это так называемые общеземные эллипсоиды (эллипсоида WGS84, широко используемого и в наши дни, в ней ещё нет, поскольку справочник был издан в 1987 году, и этот эллипсоид, как новейший стандарт, в ней упомянут отдельной строкой). Основной целью нахождения параметров общеземного эллипсоида является наилучшее приближение геоида по всей поверхности Земли. Отсюда непосредственно следуют два необходимых требования к нему: его ось вращения (малая полуось) должна совпадать с осью вращения Земли и центр обязательно совпадает с центром масс Земли. Между прочим, из этого, как мы увидим в дальнейшем, следует и то, что сам общеземной эллипсоид одновременно и определяет систему координат. Поверхность же эллипсоида (или, что то же самое, его полуоси и/или сжатие) определяется простым соотношением: он должен минимально отклоняться в среднем от поверхности геоида (математическое выражение для этого требования я здесь приводить не буду). Ключевым здесь является понятие «в среднем». Это значит, что для данной конкретной местности общеземной эллипсоид вовсе не обязан как можно более точно описывать земную поверхность в этом месте! Важно лишь минимальное отклонение, суммированное по всей поверхности Земли.

Задачу описания, или приближения к поверхности геоида для конкретной местности решают так называемые референц-эллипсоиды. Во всех приведённых таблицах все эллипсоиды, кроме двух последних, которые мы только что упомянули, и являются, фактически, референц-эллипсоидами. Исторически по-другому и не могло быть, вплоть до второй половины XX века измерения, направленные на создание моделей эллипсоидов, проводились, как правило, в каждой стране отдельно, случаи международной кооперации были единичны. Впрочем, некоторые эллипсоиды с успехом использовались и в разных странах, но понятно, что современной точности измерений при таком подходе достичь было сложно.

Из самой постановки задачи (точное описание конкретной местности: страны, региона и т.д.) следует смягчение требований к пространственному расположению эллипсоида относительно геоида. Действительно, есть тоже только два требования, но выраженные в гораздо менее жёсткой форме: по-прежнему минимизируются отклонения от геоида, но только для выбранной местности, и малая полуось обычно сохраняет параллельность оси вращения Земли (но уже не обязательно с ней совпадает). Понятно, что это смягчение приводит к следующим последствиям:

• полуоси референц-эллипсоида уже не обязаны быть равными полуосям общеземного эллипсоида, то есть размер и форма эллипсоида отличаются от общеземного
• сам референц-эллипсоид сдвинут относительно общеземного, а может быть, как мы увидим в дальнейшем, даже и повёрнут

Вышеописанные искажения и сдвиги референц-эллипсоидов относительно общеземных подробно мы рассмотрим, когда будем рассматривать системы координат. Пока же мы уже готовы ответить на вопрос, поставленный в начале главы: для чего нужны разные виды эллипсоидов?

Ясно, что для целей картографирования стран, даже самых больших, лучше всего использовать референц-эллипсоиды (вспомните ту оговорку, которую я сделал выше о том, что общеземной эллипсоид не обязан быть одинаково хорошим приближением для всех участков Земли). Никто не мешает разработать каждой стране свой референц-эллипсоид и успешно его использовать. Действительно, разработанный ещё в СССР в 40-е годы эллипсоид Красовского с успехом используется и в наши дни и по-прежнему хорош, если не требуется особая, прецизионная точность.

Если же нам нужно строить картографические изображения всей поверхности Земли или её континентов, то тут нам не обойтись без общеземных эллипсоидов. А самое главное применение они находят в разнообразных космических применениях: для расчета параметров орбит искусственных спутников Земли, задач навигации и т.д.

В следующей таблице приведены параметры самых современных общеземных эллипсоидов. Там же кратко обозначена основная цель его применения.

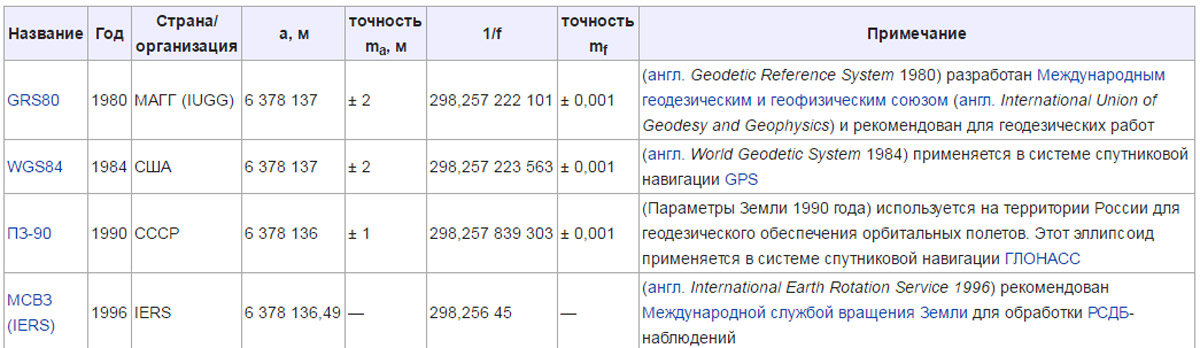
Хорошо видно, что и размеры, и сжатие эллипсоидов наконец-то практически сошлись к некоторым постоянным значениям. В самом деле, уже достигнута такая точность, что речь фактически идёт об уточнении оставшихся сантиметров полуосей (на уровне их общей величины порядка 6000 км!) и тысячных долей после запятой для параметров сжатия.

ДАВАЙТЕ ВЕРНЁМСЯ К СТАРЫМ КАРТАМ

Теперь самое время окинуть нашу обширную подборку эллипсоидов разного времени одним взглядом. Поскольку нас интересуют лишь карты, начиная от времён Российской империи до наших дней, то реальный выбор эллипсоидов у нас невелик: практически весь XIX-й век успешно использовался эллипсоид Вальбека, лишь с конца века и до 40-х годов века XX-го стал использоваться эллипсоид Бесселя. А с 40-х годов его уже сменил эллипсоид Красовского, который, как я уже упоминал, с успехом используется и в наши дни. Упомянутый в таблице эллипсоид Теннера, хотя и встречается довольно часто в литературе, по-видимому для картографических использований широкого применения не нашёл.

Легко видеть, что за время, прошедшее от времён Вальбека до Красовского большая полуось референц-эллипсоида «подросла» на 1349 м. На первый взгляд — это много, почти полтора километра. Если перевести разницу на длину «окружности» (на самом деле, эллипса) для экватора или какого-нибудь из меридианов, получим величину порядка 8,5 километров. Решительная катастрофа: представьте себе карту-километровку или близкие к ней по масштабу карты двух- и трёхвёрстки, которые «врут» на 8,5 километров!

Однако давайте теперь разберём, что значит «врать». Легко посчитать, что наши страшные 8,5 километров набегают за полную окружность, то есть за расстояние порядка 40000 км. На 40 же километров дуги окружности (порядок величины близок к характерным размерам листов, например, трёхвёрстных карт) «враньё» составит величину в тысячу раз меньшую, то есть порядка 8,5 метров. А эта величина уже меньше или равна предельной точности масштаба карты, которую мы с вами не раз обсуждали ранее!

(Продолжение следует)

Владимир Комиссаров