Загадка «проекции Мюфлинга»

ЭТОТ СТРАШНЫЙ ЗВЕРЬ МЮФЛИНГ

Кажется, безвозвратно ушли в прошлое времена, когда слова «проекция» или «система координат» повергало в священный трепет тех, кто так или иначе соприкасался с картами: путешественников, поисковиков, пеших туристов и автомобилистов, да и просто любителей карт.

Давным-давно те, кто так или иначе пользуется картами в электронном формате и навигаторами научились привязывать растровые карты, изготовленные в самых разных проекциях. Это в первую очередь касается карт исторических, таких как карты Генштаба РККА или, к примеру, военно-топографическая трёхвёрстная карта. И слова «Гаусс-Крюгер» или «Бонне» уже давно никого не пугают.

И лишь одно словосочетание вызывает буквальный ступор у многочисленных участников интернет-дискуссий. Это слова «проекция Мюфлинга». Интригу подпитывает ещё и то, что упоминаний об этой проекции нет ни в одной популярной программе, работающей с растровыми картами.

И то сказать: как быть с проекцией, про которую неизвестно ничего — ни центральный меридиан, ни главная параллель? А то ещё выясняется, что этих параметров у неё и в помине нет! Даже самые опытные пользователи в лучшем случае вам расскажут, что эта проекция является ничем иным, как рабочим планшетом топографа, только оформленном в виде карты.

ЗНАКОМИМСЯ СО ЗВЕРЕМ БЛИЖЕ

Между тем, ещё в 1936 году была опубликована брошюра¹, в которой свойства многогранной проекции, иначе называемой «проекцией Мюфлинга» по имени её создателя, были изложены с исчерпывающей полнотой. За несколько лет до этого советскими картографистами был начат масштабный проект: перевод карт, созданных в проекции Мюфлинга (она широко использовалась для создания карт крупного масштаба, начиная с начала ХХ века) на более передовую и точную проекцию Гаусса-Крюгера. Однако, прежде чем обратиться к этому материалу, повторим вкратце всё то, что стало известно внимательному читателю нашего журнала из предыдущей статьи.

Итак, проекция Мюфлинга строится так: земной шар разделяют по линиям меридианов и параллелей на «сфероидические трапеции», а затем каждую такую «трапецию» проектируют на плоскость, которая касается земной поверхности в центральной точке «трапеции». Полученная трапеция и составляет отдельный лист карты.

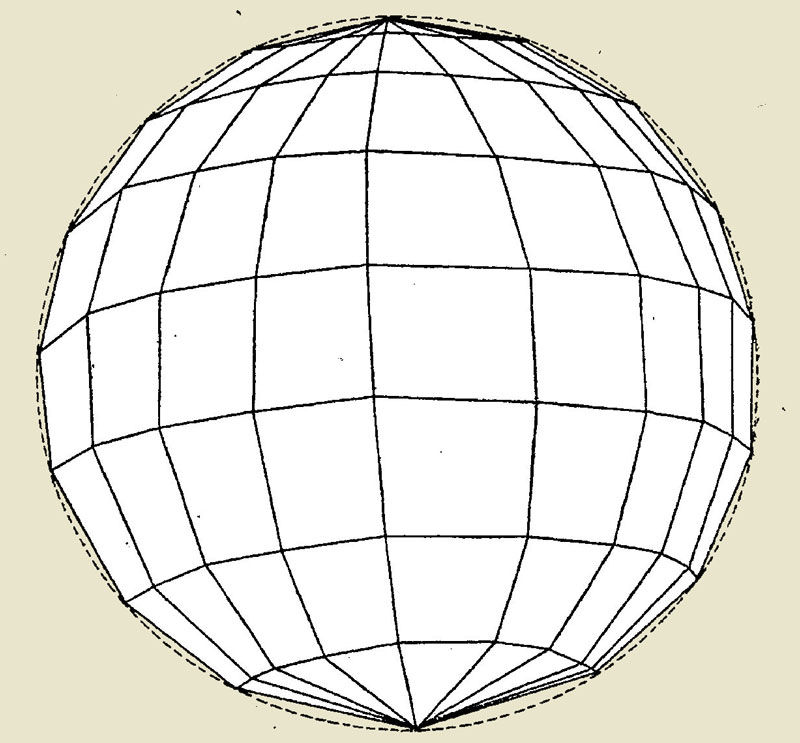
На самом деле, уже на этой стадии построение упрощают: на листе бумаги строят не криволинейную спроецированную, а прямолинейную трапецию — именно такой способ построения изложен в брошюре. Ниже приведён рисунок, поясняющий способ построения и преобразования криволинейной трапеции на сфере в прямолинейную трапецию на плоском листе:

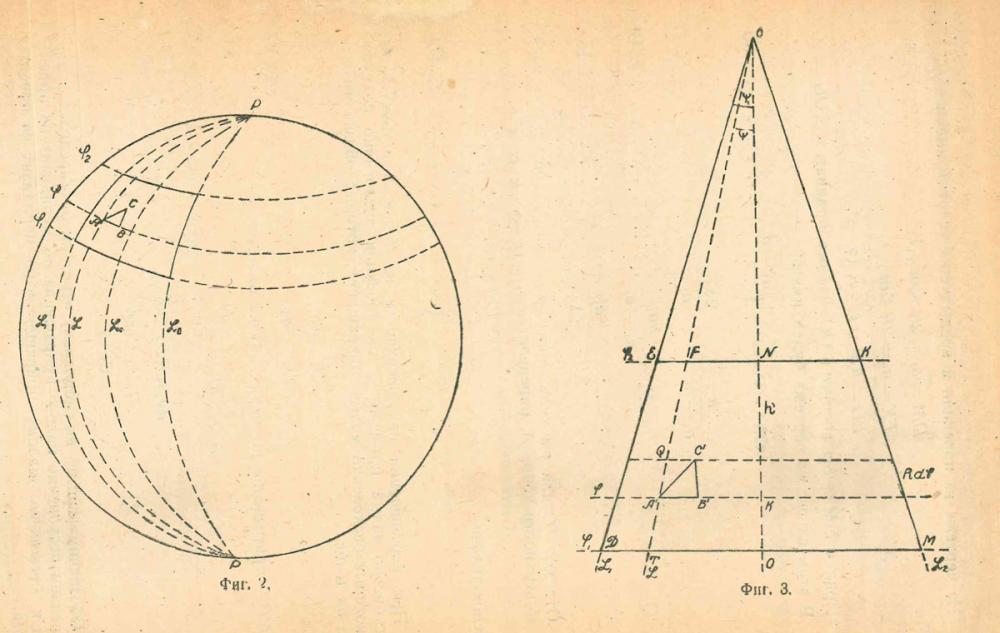
Здесь обязательно следует отметить одно не очень приятное следствие такого построения: при таком подходе невозможно соединить отдельные листы карты в одно сплошное, без разрывов, покрытие. Это хорошо иллюстрирует рисунок, приводимый ниже. Как следствие, без каких-то специальных ухищрений мы не сможем склеить отдельные листы карты в один цельный лист.

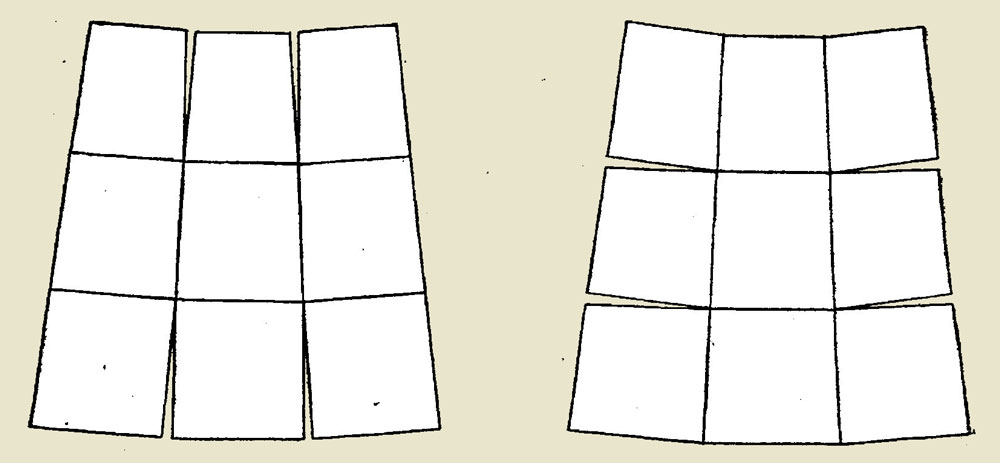
Большая часть упомянутой статьи посвящена вычислению искажений при таком подходе для построения карты двухкилометрового масштаба. И эти искажения довольно заметны: для карты-двухкилометровки они составляют до 6–8 единиц предельной точности масштаба, особенно в отдельных участках карты. Довольно поучительным является также изображение того, как соотносятся между собой две карты: построенной в проекции Мюфлинга и карты той же области, но построенной в более точной проекции Гаусса-Крюгера.

Естественно, что при увеличении масштаба карты и при одновременном уменьшении площади, покрываемой листом, такие искажения должны были бы стать меньше. В принципе, по методике, изложенной в статье, их можно было бы даже оценить количественно. Однако, рассмотрение этих искажений мы сейчас оставим в стороне, поскольку цель-то у нас другая, совершенно утилитарная: использовать те знания, которые мы получили при знакомстве с проекцией, для практической привязки карты. А в качестве подопытного образца мы возьмём один из листов двухверстовой карты Западного пограничного пространства — именно на этих картах и «спотыкается» большинство любителей картографии.

ВСЁ ГОРАЗДО ПРОЩЕ, ЧЕМ КАЖЕТСЯ

Когда не известно, с чего начать привязку, всегда полезно заняться измерениями. А прямые измерения по листам двухверстовой карты показывают совершенно удивительную вещь: разница в длинах короткой (верхней) стороны трапеции и длинной (нижней) составляет всего-навсего два с половиной миллиметра (при общей длине каждой из сторон свыше трёхсот миллиметров)! Заметим сразу же, что боковые стороны трапеции равны друг другу на уровне точности примерно 0,2 мм — что как раз и равно предельной точности печатных карт. Стоит напомнить также, что стороны, ограничивающие трапецию — это линии параллелей и меридианов.

Итак, из измерений следует, что наша трапеция — это почти в точности прямоугольник! И вполне естественной идеей было бы эту трапецию полностью в идеальный прямоугольник и превратить! Это немедленно даст нам два существенных преимущества: во-первых, прямоугольная сетка характерна для простых цилиндрических проекций, например, меркаторской, а во-вторых, прямоугольные листы уже можно состыковать в одно непрерывное покрытие.

Если мы представим себе трапецию, изображённую на куске резиновой плёнки, то такое преобразование в прямоугольник выглядело бы очень просто: мы просто немного растянем верхнюю сторону трапеции на те самые 2,5 мм — ровно до ширины нижней стороны. Причём, все промежуточные области внутри трапеции растянутся строго пропорционально (из этого, в частности, следует то, что любая прямая линия внутри границ трапеции перейдёт строго в прямую внутри прямоугольника, то есть наше растяжение будет в этом смысле строго линейным).

Для описанной операции можно было бы воспользоваться любым графическим редактором, позволяющим растягивать растр. Однако, мы поступим ещё проще. Вспомним о том, что достаточно «умные» программы привязки карт умеют работать с растром как раз в нужном нам направлении. Таков, к примеру, неоднократно использовавшийся нами Global Mapper. Программа умеет легко «натянуть» растр на указанные ей точки привязки. А упомянутая выше линейность преобразования трапеции в прямоугольник послужит гарантией того, что и преобразование растра вдали от точек привязки будет однозначным, предсказуемым и, самое главное, — пропорциональным.

УКРОЩАЕМ ЗВЕРЯ

Мы уже не раз писали о привязке карт в Global Mapper, поэтому здесь подробно на деталях операций останавливаться не будем — они абсолютно одинаковы с изложенными в предыдущих статьях. Начнём описание методики сразу с того, что мы открыли нашу подопытную карту в окне привязки (калибровки). Прежде, чем начинать привязку, как обычно, укажем систему координат и проекцию.

В качестве системы координат вполне логично взять СК, основанную на эллипсоиде Бесселя: в начале XX века это наиболее устоявшийся эллипсоид в российской картографии. Естественно, никаких сдвигов этого эллипсоида мы не задаём: используем ту самую СК с нулевыми сдвигами, которую мы создали в одной из предыдущих статей.

Какую нам выбрать проекцию? На самом деле, подойдёт любая цилиндрическая — нам важно лишь, чтобы у неё сетка координат была строго прямоугольной. Но тогда логичнее всего взять одну из самых простых и распространённых — меркаторскую.

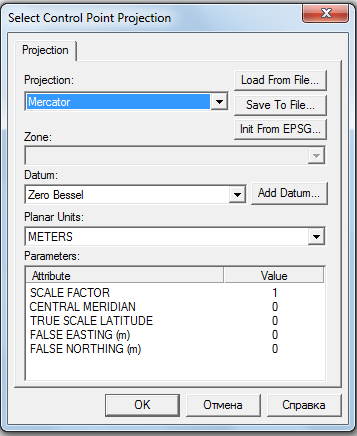
После выбора системы координат и проекции у нас почти всё готово к привязке карты. Правда есть ещё одна деталь: долготы на нашей карте указаны не от Гринвичского меридиана: во время её создания этот стандарт в СССР ещё не устоялся окончательно и на двухверстовой карте используются долготы от Пулково. Можно было бы сразу пересчитать их в «гринвичские» и вводить эти величины сразу при привязке, но мы снова поступим проще, по той методике, которую использовали при привязке трёхвёрстной карты — переведём долготы в «Гринвич» позже и одной операцией.

Итак, обычным путём начнём расставлять точки привязки. Поскольку качество растра у нас очень хорошее, без видимых искажений, склеек и т.п., нам для привязки вполне хватит 4 точек по углам карты.

В конце концов, после расстановки точек у нас должна получиться следующая табличка:

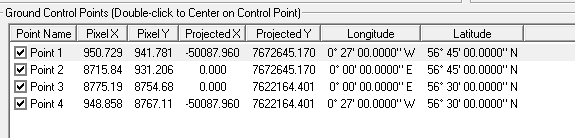
Наступает торжественный момент. Сохраним привязку; нам предстоит оценить не только её качество, но и то, насколько хорошо Global Mapper понял ту задачу, которая перед ним стояла: растянуть трапецию в прямоугольник. На рисунке ниже мы специально включили градусную сетку с интервалом в 1 угловую минуту.

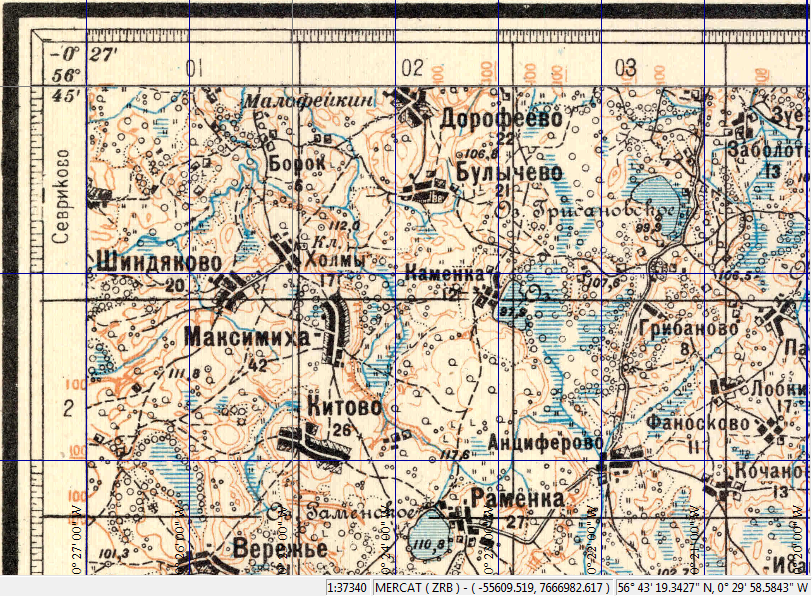
Можно видеть, что крайние линии сетки совершенно идеально совпадают с границами карты — а это значит, что Global Mapper с задачей преобразования проекции Мюфлинга в проекцию Меркатора справился на пять баллов. Кроме того видно, что и зарамочные отметки минут на карте также совпадают с линиями сетки меркаторской проекции. Это говорит о том, что и растяжение растра прошло так, как нам и требовалось, то есть строго пропорционально.

Дальнейшие операции будут вполне рутинными. Известным уже нам способом изменим долготы от Пулкова на долготы от Гринвича. Правда, на этот раз, для разнообразия, возьмём немного другое значение для разности долгот. Как мы уже писали раньше, это не очень принципиально, поскольку любая неточность может быть скомпенсирована точным расчётом сдвига СК. Так вот, в данном случае выберем значение предложенное Стрельбицким — по-видимому, на момент создания двухвёрсток оно было наиболее актуальным. Итак, вновь откроем окно калибровки карты, в нём — окно проекции и для значения центрального меридиана подставим величину 30°19'40.16''. После пересчёта программой координат долгот получим новую табличку точек привязки.

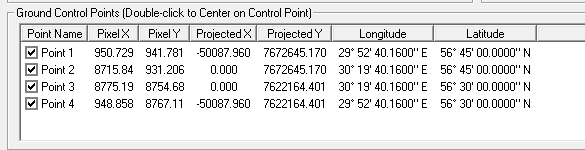
Вновь сохраним привязку и перейдём в рабочее поле программы. Теперь видно, что линии сетки широт по-прежнему совпадают с сеткой карты, а линии долгот сдвинулись. Как указывалось раньше, так и должно быть: ведь введённая нами разница между центральными меридианами не выражается целым числом минут.

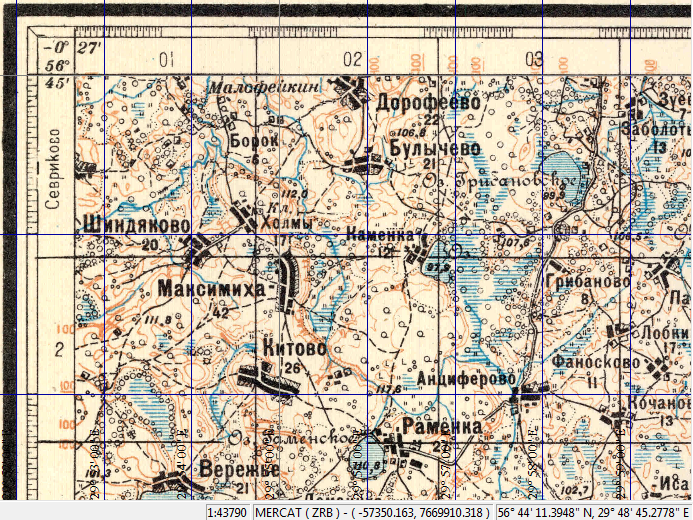
Теперь наша карта имеет вполне современные координаты и мы уже можем примерить на неё современный трек (он есть у нас под рукой — мы его получили в недавнем путешествии в Полистовский заповедник). Как и следовало ожидать, видна некоторая систематическая ошибка — сдвиг карты в основном в восточном направлении.

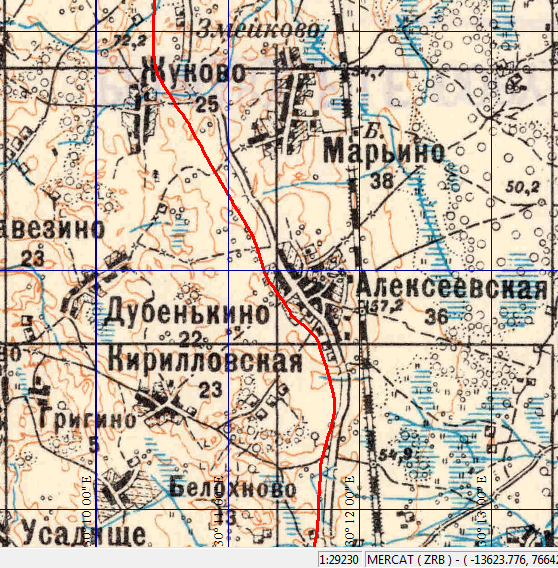
Далее, чтобы точнее привязать карту следовало бы вычислить параметры сдвига проекции. Для этого надо было бы найти на карте некоторые объекты, которые точно сохранились до нашего времени, определить их координаты по карте и сравнить с современными координатами в системе WGS84. Но мы сейчас этим заниматься не будем: такие вычисления будут темой наших следующих статей. Вместо этого, лишь для демонстрации метода, просто используем систему координат, вычисленную раньше для листа карты Генштаба РККА. Снова перейдём в окно калибровки и заменим систему координат, построенную на эллипсоиде Бесселя с нулевыми сдвигами на СК с параметрами 359,48; 144,91 и 583,85.

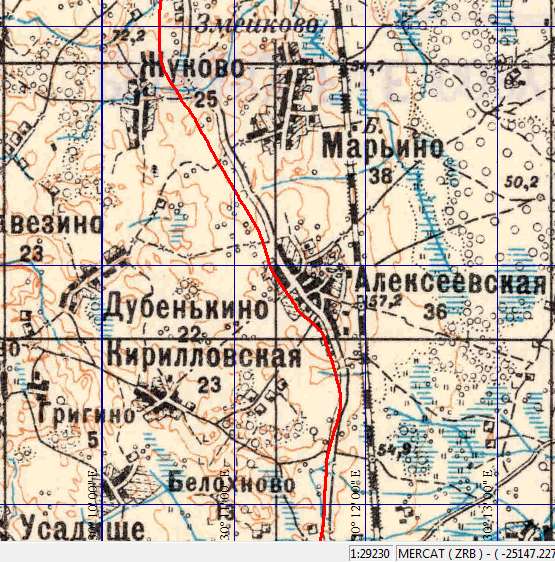
Видно, что хотя и идеального соответствия трека карте добиться не удалось (этого и нельзя было бы ожидать, поскольку мы выбрали СК немного не соответствующую времени создания карты, а следовательно, имеющую несколько иные параметры), но «восточный сдвиг» сильно уменьшился. А более точное решение мы найдём несколько иными методами, чем это делали ранее — и о таких методах мы расскажем в совсем недалёком будущем.

Примечания

¹ Г.М. Кирьяков. Исследование искажений многогранной проекции Мюфлинга и их влияние на точность составления карты масштаба 1:200000, Новосибирск, Москва, Ленинград, Грозный, 1936 г.

Владимир Комиссаров