Привязка исторических карт. Часть II, практическая. Привязываем трёхвёрстки
В предыдущей статье мы вкратце коснулись теоретических аспектов привязки исторических карт. Теперь перейдём к практическим действиям: на примере трехверстной военной топографической карты западной части Российской империи пройдём все этапы правильной привязки.
Шаг первый.
О проекции и системе координат военных трёхверсток у нас имеется вся необходимая нам информация. Они созданы в проекции Бонна, для главной параллели которой выбрана широта 52о, центральным меридианом ("условный ноль" долготы) является Пулковский, и, наконец, в качестве эллипсоида системы координат, судя по параметрам, приведённым на картах, выбран эллипсоид Вальбека.
В первую очередь, нам нужно будет настроить наш картографический инструментарий. В качестве такового мы будем использовать программы Global Mapper и OziExplorer, как наиболее доступные и широко используемые любителями. Нам нужно будет создать в этих программах нужные системы координат и настроить координатную сетку для удобства работы.
Проще всего это делается в программе OziExplorer. С недавнего времени, там уже существует эллипсоид Вальбека, да не один, а целых два. Различие их в том, что для первого использовано значение большой полуоси в 6376896 метров, как впервые приведённое Ф.Н. Красовским в своём учебнике. Между тем, если взять этот размер и размер эллипсоида, приведённый в саженях (2988853 сажени), то для значения сажени мы получим 2,13356 метра. Однако, правильней и удобней считать сажень равной 2,1336 метра ровно, так как это даст нам ровное значение дюйма в 2,54 сантиметра (считая в сажени 84 дюйма), что гораздо ближе к современным эталонам. Именно поэтому в OziExplorer и введён второй эллипсоид Вальбека с полуосью в 6377016,7608 метров и именно им мы и будем пользоваться. Такая неоднозначность смущать не должна, поскольку во времена создания трёхвёрсток точного эталона метра ещё не существовало, да и разница между полуосями составляет всего 121 метр, следовательно погрешность на каждый лист карты (около 1 метра) будет меньше предела точности самой карты и разрешения её скана.
Итак, создаём в корневой папке программы OziExplorer пустой текстовый файл с названием datums.dat и прописываем в него следующие строки:
ZW, 31, 0, 0, 0
ZW2, 32, 0, 0, 0
Здесь ZW - наше условное название системы координат (от Zero и Walbeck), первое число после запятой - номер эллипсоида, присвоенный в программе, а дальнейшие нули - параметры смещения СК относительно системы WGS84. Мы сейчас не будем заниматься преобразованием одной системы в другую, поскольку эти параметры нам неизвестны, их нам только предстоит вычислить. Когда карта уже будет привязана в этой системе координат, мы сможем рассчитать нужные поправки.
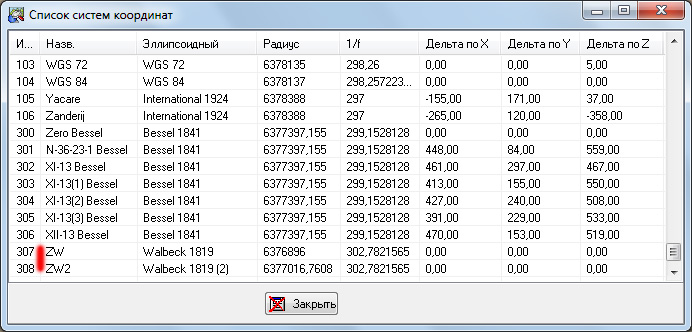
Запустив OziExplorer и открыв пункт меню "Просмотр" - "Список систем координат" мы увидим в этом списке наши СК:
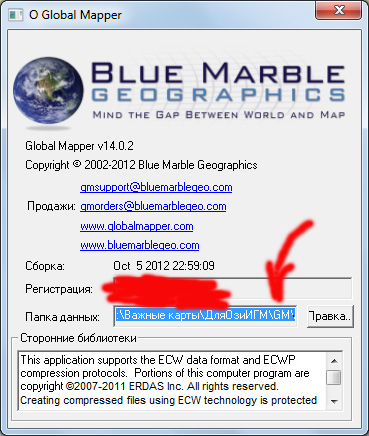
В Global Mapper создать нужную СК немного сложнее, поскольку встроенного эллипсоида Вальбека в программе нет, но и создать его нетрудно. Для начала создадим рабочую папку программы, в которой мы будем хранить наши пользовательские данные. Это нужно для того, чтобы без излишних проблем обновлять или переустанавливать программу и не настраивать программу заново. Папку можно создать в любом удобном месте на компьютере, а затем, открыв пункт меню "Справка" - "О программе" указать в ней нужный путь:
Теперь создадим в рабочей папке два файла с именами custom_ellipsoids.txt и custom_datums.txt. В первом будут храниться параметры наших эллипсоидов, а во втором - созданные нами системы координат. В файл custom_ellipsoids.txt вписываем следующие строки:
"Walbeck 1819",6376896.00000000000000000,6355834.997
"Walbeck 1819 (2)",6377016.76080000030000000,6355955.359
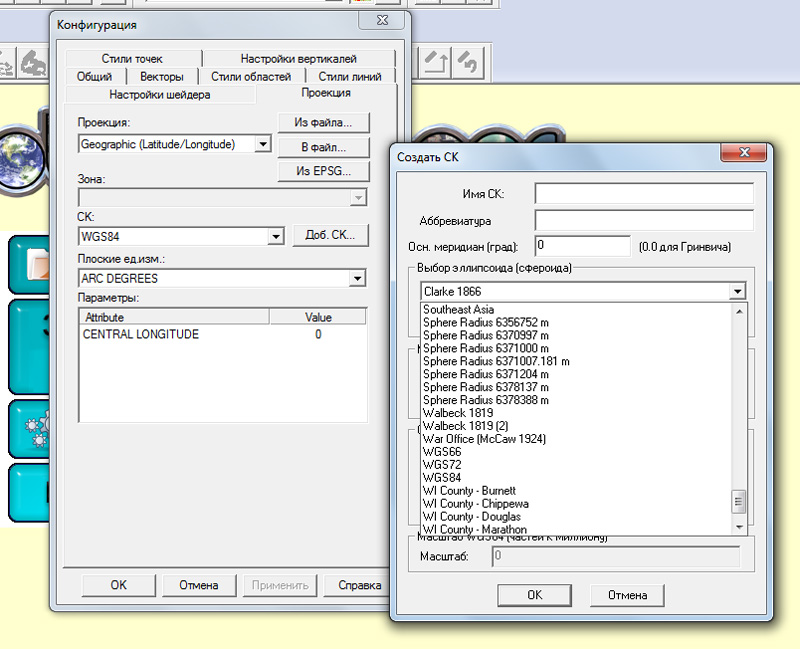
И в диалоговом окне настройки системы координат мы сможем выбрать любой из созданных нами эллипсоидов:
В файл custom_datums.txt добавим строки:
"ZW","ZW","Walbeck 1819",0.00000000000000000,0.00000000000000000,0.00000000000000000
"ZW2","ZW2","Walbeck 1819 (2)",0.00000000000000000,0.00000000000000000,0.00000000000000000
Следует обратить внимание, что системы координат мы назвали в точности так, как в программе OziExplorer. Это нужно для того, чтобы каждая из программ без проблем могла читать файлы привязок, созданные другой программой. Кроме того, крайне желательно именовать СК максимально просто, почему это так - станет понятно из дальнейшего изложения.
Теперь в списке систем координат мы увидим обе созданные системы:

Эллипсоиды и системы координат можно также создать и средствами диалоговых окон настроек проекции, которые показаны выще, но проще взять уже готовые данные.
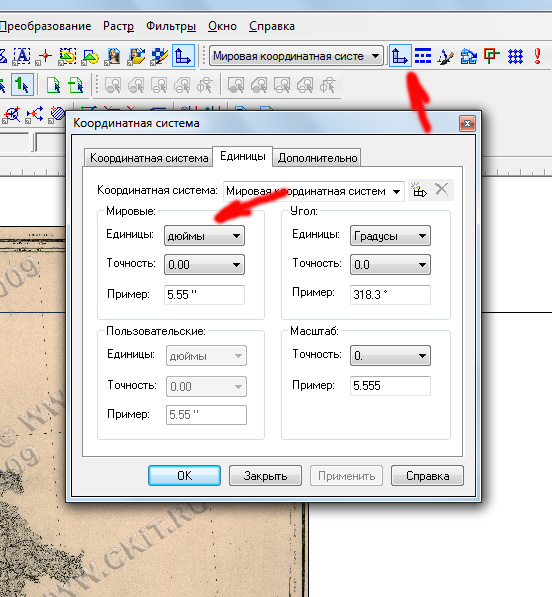
Нам остаётся настроить координатные сетки и единицы измерений. Поскольку основной программой, в которой мы будем привязывать карты будет Global Mapper, то "озик" пока трогать не будем. Во-первых, в Global Mapper количество точек привязки не ограничено 9-ю, как в OziExplorer, а во-вторых, мы будем использовать для привязки не только градусную сетку, имеющуюся на карте, но и использовать координаты углов карты, рассчитанные в единицах длины. Такое совместное использование градусных и линейных единиц возможно только в Global Mapper. Наконец, в-третьих, нам для контроля качества работы потребуется попеременно отображать градусную и прямоугольную сетки, а у OziExplorer с этим существуют серьёзные проблемы: мало того, что в эта программа может построить пользовательскую сетку не для всех проекций и не для всех масштабов карт, но ещё и единицы измерения этой сетки ограничены километрами и метрами. Поскольку мы должны настроить программу для работы в футах (о чём подробнее чуть ниже), нам этот вариант не очень подходит. Поэтому в Global Mapper на вкладке "Общий" конфигурации выставим для показа сетки "Текущая проекция" и желаемый масштаб.
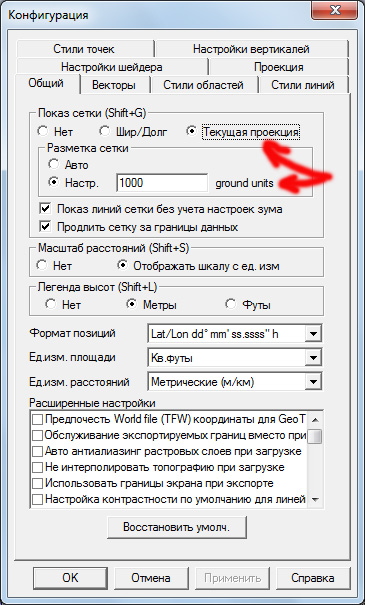
Для удобства вычислений на закладке "Проекция" при каждом первом открытии карты мы будем выставлять для плоских единиц измерения международные футы.
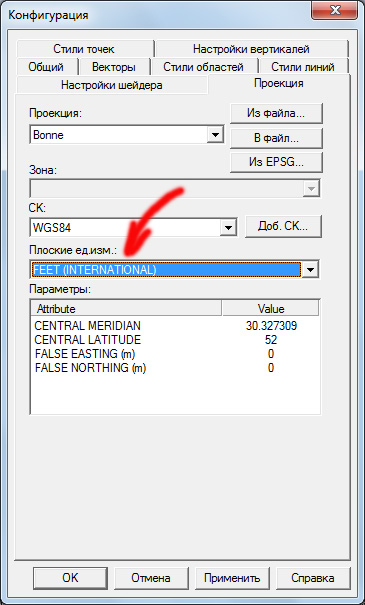
Почему именно футы, ведь на трёхвёрстках все расстояния даны в вёрстах и саженях? На этом моменте стоит остановиться подробнее. К сожалению, Global Mapper не "знает" вёрст, но дело в том, что можно пользоваться очень простыми соотношениями:
1 британская миля = 5280 футов = 63360 дюймов
1 верста = 500 саженей = 3500 футов = 42000 дюймов
Все соотношения ровные и широко применялись в XIX веке. При этом, как уже было отмечено выше, использование для дюйма значения ровно в 2,54 современных сантиметра даёт вполне однозначную и точную связь современных километров и миль, а следовательно и вёрст. Во всяком случае, именно эти коэффициенты "зашиты" в Global Mapper.
Шаг второй.
Теперь мы займёмся подготовкой растров. Сразу нужно сказать: исходное качество растра определит успех и точность всей дальнейшей нашей работы. Именно поэтому, как минимум, нужно выбирать растры, не содержащие явно выраженных склеек и разрывов: такие дефекты принципиально не устранимы и, в конечном итоге, скажутся на результате. Напротив, "гладкие" дефекты, такие как трапециевидные и подушкообразные искажения, скошенность и т. д. легко убираются именно на этом этапе. Как раз сейчас мы этим и займёмся. Но, прежде, чем приступить к работе, подчеркну: ни один растр не свободен от дефектов. Подробнее на этом я останавливался в предыдущей статье, сейчас лишь запомним: нашей задачей на этом этапе не является глубокая обработка растра; мы лишь в щадящем режиме исправим те ошибки, которые возникли либо в результате сканирования или фотографирования, либо были изначально присущи самому исходному бумажному материалу (например, изменения пропорций листа со временем). Наша задача - не ухудшить исходный материал, а лишь максимально приблизить его к тому материалу, который был первоначально задуман и создан картографами; тем самым мы ещё и облегчим в дальнейшем труд нашей программы привязки, которой не придётся беспокоится о коррекции растра "на лету". Поэтому и для дальнейшей работы мы возьмём не широко представленные в сети сканы трёхвёрсток (они, как не раз подчёркивалось, имеют грубые неустранимые дефекты склейки из фрагментов), а вполне оригинальные платные растры, основным достоинством которых является то, что они отсканированы целиком.
Работу по исправлению сканов будем вести в Spotligt Pro: эта профессиональная программа как раз и предназначена для таких целей. Первый инструмент нам уже подготовлен разработчиками. Он называется "Автокоррекция". Для наших целей нам достаточно установок инструмента по умолчанию. Он устранит имеющийся перекос растра, немного удалит имеющийся на растре "мусор" и слегка подправит гистограмму изображения. Загрузив в программу исходный скан, запустим инструмент:
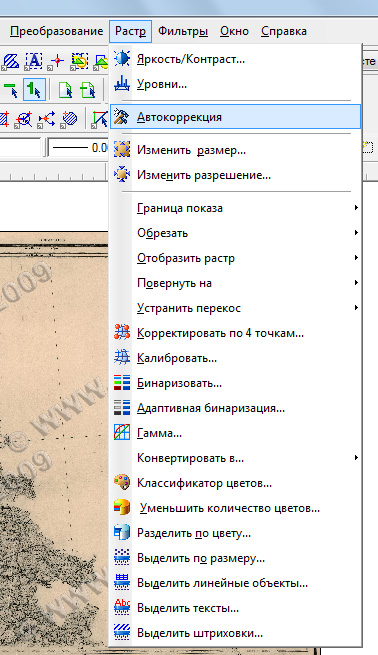
Инструмент "Автокоррекция" хорошо удаляет перекосы скана, которые возникают при смещении документа в сканере. Однако, он не в состоянии побороть трапециевидные искажения, а также приблизить размер растра к оригинальному (нужно помнить, что многие сканеры, особенно барабанные, вносят такие искажения). Для этого существует второй очень важный инструмент, который корректирует файл изображения по 4 точкам, выравнивая эти точки по углам прямоугольника. При этом есть возможность задать размер этой прямоугольной рамки, тем самым "подогнав" размер изображения максимально близко к оригиналу:
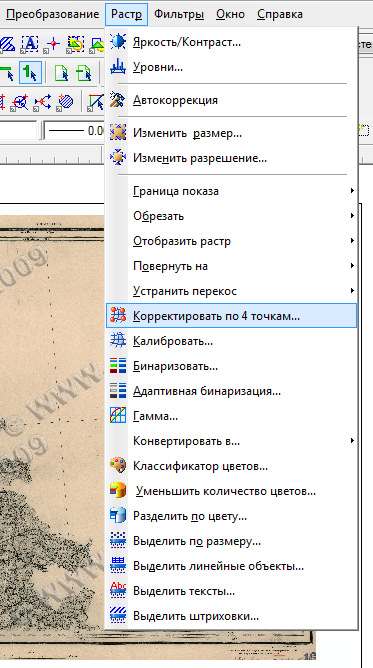
Запустив инструмент, мы увидим окно настройки параметров выравнивания, где самым важным для нас будет размер рамки для выравнивания. Укажем его вручную, исходя из имеющихся данных для трёхвёрсток:
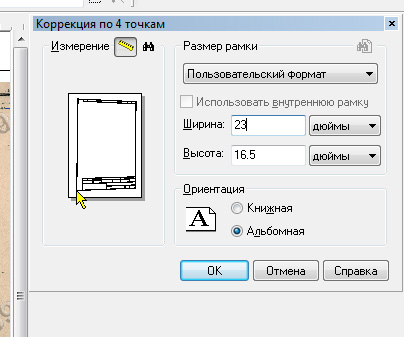
Далее, максимально увеличив растр до распадения на пиксели, отметим точки выравнивания на внутренней рамке карты и запустим выравнивание. По окончании процесса, чтобы убелиться в том, что наш растр приобрёл нужную нам исходную геометрию, настроим линейки размеров программы:
...после чего, прикладывая изображение к линейкам, удостоверимся, что всё было сделано правильно:
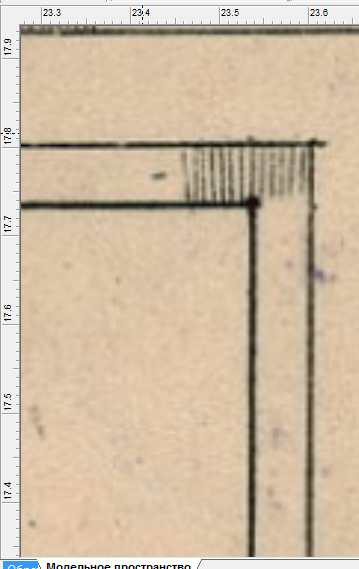
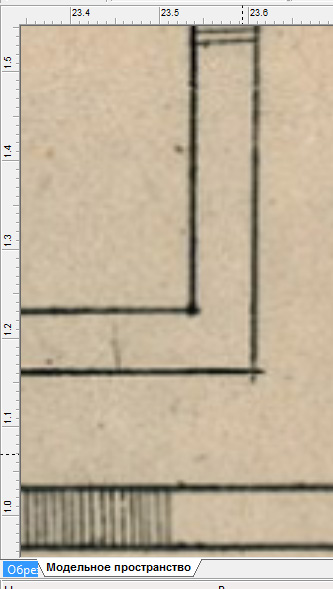
Напоследок запустим инструмент автоматической обрезки изображения. В автоматическом режиме он уберёт излишки полей белого цвета, которые могли получиться при предыдущих исправлениях.
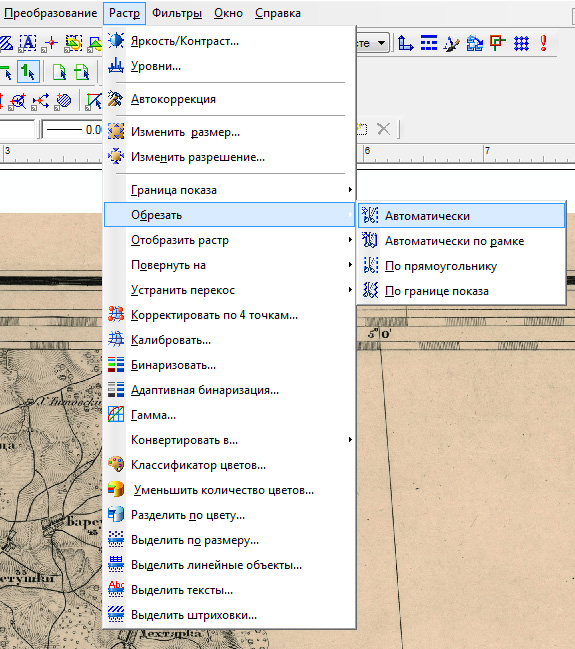
Нам остаётся только сохранить исправленный растр. Выбор показанных на рисунке параметров даст файл, размер которого максимально близок к размеру исходного растра. Для дальнейшей работы нам этого качества вполне будет достаточно:
Итак, в результате мы получили изображение практически идеальной прямоугольной формы и нужных нам пропорций, не ухудшив визуального восприятия растра, в чём легко убедиться, посмотрев на исходное и конечное изображения (приведены в разрешении, уменьшенном с 300 до 100 точек в дюйме):
Если продолжить внимательное сравнение двух растров, то мы заметим, что изображение по высоте изменилось гораздо меньше, чем по ширине (1,0% против 2,6%):
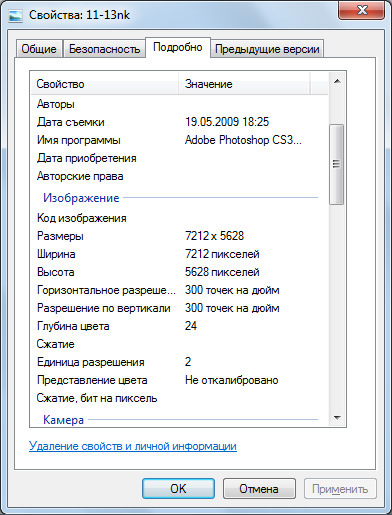
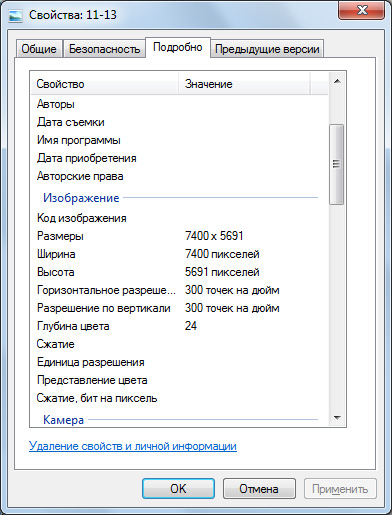
В верности такого изменения можно было бы убедиться в Spotligt Pro, прикладывая линейку масштаба карты к измерительным линейкам на экране до выравнивания растра по рамке...
... и после:
Напоследок ещё раз подчеркну: на этом шаге мы лишь исправили то, что сделали время и природа с исходным бумажным оригиналом, а также немного поправили ошибки техники. То есть, фактически, привели изображение карты к тому, как оно должно выглядеть изначально. Для привязки нам большего не нужно; если же в дальнейшем понадобятся более глубокие изменения растра (например, перевод в чёрно-белую палитру или сохранение в ином формате), их всегда можно сделать, не нарушая привязки. Важно лишь затем сохранять растр в тех пропорциях и размерах в пикселях, в которых осуществляется привязка. Дальнейшая "подмена" одного файла изображения другим никак не скажется на точности привязки.
Шаг третий.
Теперь, когда мы настроили программы и имеем готовый картографический материал, можно заняться оценкой той точности, с которой нам предстоит работать. Понятно, что она должна быть выше, чем ошибки в исходном материале - только так можно гарантировать себе нужный результат. Но нам нужна количественная оценка этой точности. При этом нам нужно будет различать точность исходного картографического материала (бумажной карты) и разрешение растра - её электронной копии.
Достаточно хорошо известно, что на любом чертеже или карте нельзя обычными средствами ("циркулем и линейкой") измерить расстояние меньше 0,2 мм. Расстояние на местности, соответствующее этой величине называют предельной точностью масштаба карты. Поэтому и современные печатные карты изготавливают с учётом этой точности. Вполне разумно предположить, что точность изготовления листов военных трёхвёрсток вряд ли была больше, учитывая технологию тогдашней печати с гравированных медных листов. Ещё нужно иметь в виду, что эта точность - предельная, реально из-за возникновения погрешностей при составлении карты и её печати ошибки могут достигать 0,5-0,75 мм. Но мы возьмём в качестве оценки точности исходного картографического материала именно нижнюю границу: 0,2 мм. Применительно к масштабу трёхверстовой карты это даёт примерно 0,01 дюйм, что соответствует 0,03 версты на местности или 15 саженей (32 метра). Если мы обеспечим точность работы, заведомо лучшую этой величины, мы гарантируем себе хороший результат.
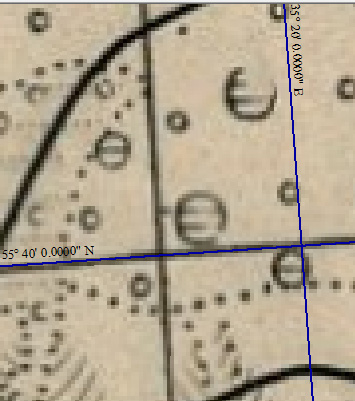
Посмотрим теперь, как соотносится наша электронная копия карты с рассуждениями, приведёнными выше. Разрешение растра составляет 300 точек на дюйм, следовательно 1 пиксель карты соответствует 1/300 дюйма на карте или 1/100 версты на местности. То есть, разрешение растра втрое превышает предельную точность масштаба карты. Именно поэтому любая, самая тонкая линия на карте имеет толщину в 3-4 пикселя. Так выглядят, например, линии широты и долготы при достаточном увеличении:


Таким образом, стараясь работать "с точностью до пикселя" мы заведомо обеспечим нужный результат. Причём даже, ошибившись на один-два пикселя, мы всё равно не выйдем за рамки предельной точности масштаба исходной карты. Поэтому для расстановки точек привязки достаточно брать примерные середины линий, которые легко определяются при должном увеличении. При таком подходе мы не увеличим погрешностей карты в 30 (нижняя оценка) - 90 (верхняя оценка) метров. Кстати, именно пользуясь этими соображениями в начале статьи мы пренебрегли различиями между двумя вариантами эллипсоида Вальбека - погрешность на лист получается около 1 метра, что гораздо лучше предельной точности масштаба карты.
В конце этой части хочется привести несколько примеров того, как все вышеизложенные соображения теряют смысл, когда применяются либо негодный картографический материал, либо негодная методика. Я уже не раз писал о том, что в сети широко представлены карты, грубо склеенные в графическом редакторе. В Spotlight Pro легко оценить величины ошибок склейки. Ниже приведены фрагменты той же карты, что и наша рабочая, но полученной из другого источника:


Измеренные величины разрывов в обоих случаях оказались равными 0,027 дюйма (86 метров на местности), что, фактически, находится на верхней границе оценки предельной точности масштаба карты. Это значит, что ошибку исходного картографического материала мы, как минимум, удвоим.
Второй пример связан с тем, как легко ошибиться, приняв в качестве точек привязки любые объекты, не связанные с координатными линиями или рамкой карты. Если говорить в общем, то самыми точными объектами на любой рисованной или печатной карте являются именно рамка карты и, далее - линии координат (географических или координат проекции). Это связано с тем, что вначале изображаются именно они, а все остальные объекты карты переносятся на лист, привязываясь путём расчётов, именно к рамке и к координатной сетке. А при использовании привязки "по объектам" зачастую забывают, что мосты, излучины и устья рек, перекрёстки и т.д. за столетия сильно меняют своё местоположение. На нижеприведённой карте за недостатком точек привязки по координатной сетке использовались несколько перекрёстков дорог, подобно этому:
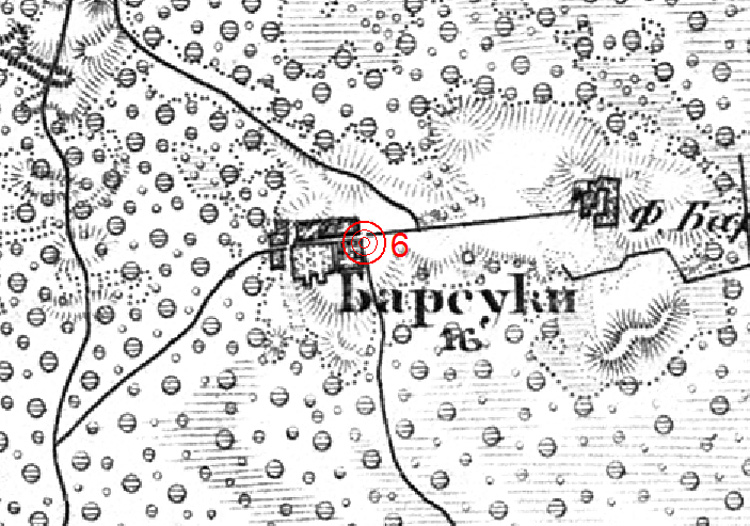
Это привело к тому, что карта в Global Mapper выглядит так:

Здесь мало того, что линии прямоугольной сетки проекции не параллельны рамке карты, но и сам растр катастрофически исказился программой. Это произошло потому, что она изо всех сил пыталась "натянуть" растр, изначально имеющий удовлетворительную геометрию, на негодные точки привязки, имеющие ошибочные сопоставления координат с реальной местностью.
Шаг четвёртый.
Теперь пришло время определиться с точками привязки нашей карты. Мы специально возьмём "трудный" лист (он приведён выше) - лист 11-13. Особенность его в том, что на него попала только одна параллель и три линии меридианов (точнее, три "полных", пересекающих весь лист, и одна "неполная", в нижнем левом углу карты). Соответственно, мы имеем только три точки пересечения и только три точки для привязки. Но и это не всё - точки лежат на одной параллели, а значит - почти на прямой (точнее, на очень пологой дуге). При такой конфигурации точек хорошая привязка становится невозможной. Как же нам быть?
На помощь нам придёт простой факт. Сами листы трёхвёрстки представляют собой регулярную сетку в прямоугольных координатах, что делает возможным расчётным путем определить расстояния углов любого листа карты от условного "нуля" отсчёта, которым в нашей проекции Бонна является пересечение 52-й параллели с нулевым Пулковским меридианом. В расчётах нам поможет специально разработанный для этих целей калькулятор. Более того, с его помощью мы сможем определить не только координаты углов листа (что даст нам дополнительные 4 точки привязки), но и точки пересечения единственной параллели с рамкой карты (ещё 2 точки) и меридианов с рамкой (ещё 7 точек). Таким образом, число точек привязки достигнет 16-ти, при этом они будут располагаться достаточно равномерно по площади листа - и этого нам вполне хватит. Калькулятор уже настроен на работу в футах, в них и будем вести все расчёты. Почему это удобно, я объяснил в самом начале статьи.
Шаг пятый.
Итак, мы, наконец, подошли к главной части нашей работы: собственно привязке карты. Запустим Global Mapper и откроем в нём наш скорректированный на предыдущих шагах растр. Поскольку никакой привязки нами ещё не создано, программа предложит нам выбрать дальнейшие действия с растром:
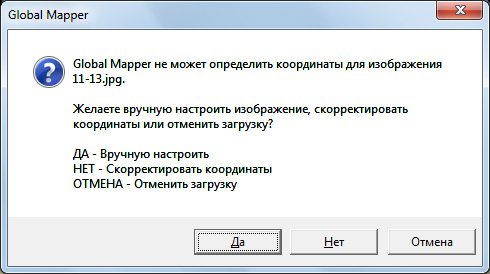
На этот вопрос следует ответить "Да", после чего откроется окно корректировки (привязки) изображения:

Программа ещё не знает ничего о проекции карты и сейчас мы это ей объясним. Нажмём кнопку "Выбор проекции" и в открывшемся окне введём требуемые параметры проекции:

В качестве системы координат выберем созданную на шаге 1 СК ZW2 и сразу же выставим линейные единицы измерения - международные футы, как говорилось выше. Главная параллель у нас имеет величину в 52о, а вот для центрального меридиана проекции мы пока оставим нулевое значение. Почему?
Дело в том, что градусная сетка на трёхвёрстках измеряется от Пулковского меридиана. Можно было бы сразу для всех линий на карте пересчитать значения долгот от Гринвича и при привязке пользоваться уже пересчитанными значениями. Но мы поступим проще: привяжем карту именно в той СК, какая имелась во время её создания, а потом одним движением изменим все " пулковские" значения долгот на величины "от Гринвича". В конце концов, вводить "круглые" значения гораздо удобнее и риск ошибиться при вводе меньше. Кроме того, при таком подходе нам будет проще контролировать качество привязки на разных этапах, в чём мы убедимся немного позже.
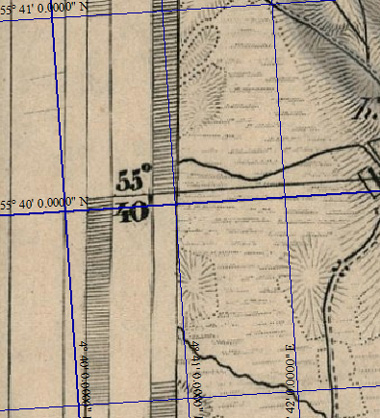
Итак, находим на нашей карте первое пересечение линии широты с меридианом, увеличиваем его до нужного масштаба и проставляем первую точку. Точки ставим на примерные середины линий:
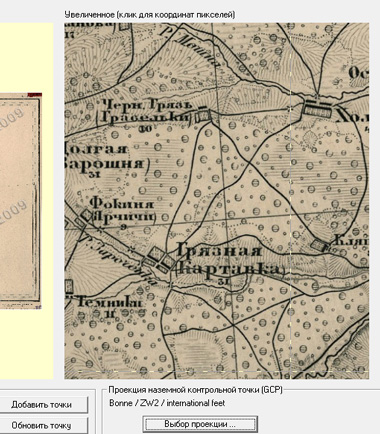

В окошках ввода контрольной точки сразу же появляются её координаты в пикселях. Нам надо сопоставить им реальные координаты на местности. Введём их в соседние окошки:
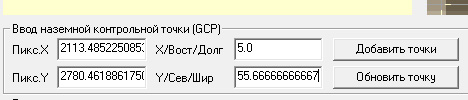
Если мы будем вводить координаты в том виде, как показано, в градусах с десятичной точкой, Global Mapper "сообразит", что они похожи на значения в градусах и на всякий случай задаст уточняющий вопрос:
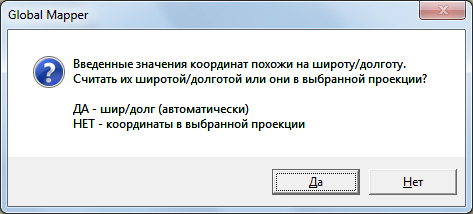
Конечно, на него следует ответить "Да", после чего точка привязки появится в списке контрольных точек:

Видно, что программа совершенно верно интерпретировала наши введённые величины. Кроме того, появились и рассчитанные значения координат в линейных единицах (футах) от точки пересечения главной параллели с центральным меридианом проекции. Точно так же вводим значения и для двух других пересечений параллели с меридианами, создавая ещё две точки привязки:

Если задано меньше 2 точек привязки, Global Mapper не даст закрыть окно корректировки изображения. Но мы ввели больше, поэтому можно нажать кнопку "ОК" и посмотреть, что у нас получается:
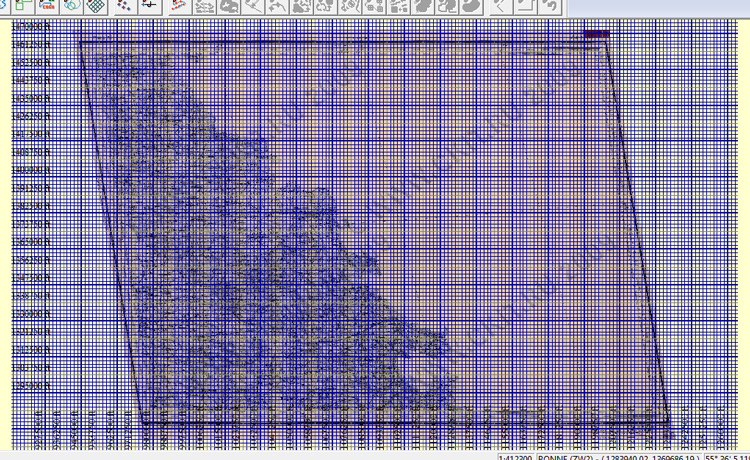
Видно, что карта довольно сильно исказилась. Это объясняется тем, что 3 точки привязки у нас лежат практически на прямой и задача, как выражаются математики является "плохо обусловленной". Нам это пока не важно, вводом следующих точек мы ситуацию исправим. Пока же следует сказать, что искажение происходит только отображения растра на экране, до тех пор, пока мы его не экспортировали, исходный растр остаётся нетронутым. Поэтому мы можем прервать работу в любой момент, сохранив рабочее пространство (меню "Файл"):
Чтобы заново вернуться в окно корректировки изображения, нужно в "Центре управления оверлеями" открыть меню правым кликом мыши и выбрать в нём первый пункт: "Изменение позиции/проекции слоя".
Теперь привяжем углы рамки. Для начала откроем калькулятор и в части "Расчёт рамки в линейных единицах" введём нужные обозначения нашего листа:
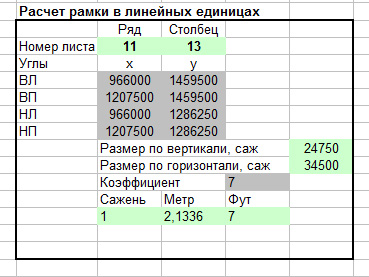
Поскольку калькулятор уже настроен на работу в футах, для углов рамки мы сразу же получим нужные значения линейных (прямоугольных) координат, то есть расстояния углов от центра проекции. Эти значения достаточно приписать точкам, лежащим на углах рамки карты. Но прежде посмотрим детальнее на ту привязку по трём точкам, которая у нас уже получилась.
Тут следует обязательно сказать о том, что, когда мы настраивали единицы разметки пользовательской сетки, мы могли указать любое число. Однако, всего удобнее нам указать величину шага в 1750 футов. Дело в том, что эта величина равна 250 саженям, что, в свою очерель, равно ровно 0,5 версты. Это значит, что на лист карты будет укладываться целое число квадратов сетки, поскольку размеры рамки кратны половине версты. Кроме того, центральный меридиан проекции проходит ровно по границе между 8 и 9 листами, а 19-й ряд карт устроен так, что главная, 52-я параллель делит края 8 и 9 листов в соотношении 21:28,5 вёрст, следовательно "сверху" и "снизу" от главной параллели укладывается целое число полуверстовых квадратов. Всё сказанное приводит к тому, что линии такой сетки должны полностью совпадать с рамкой любого листа карты, и это будет хорошим критерием качества нашей привязки.
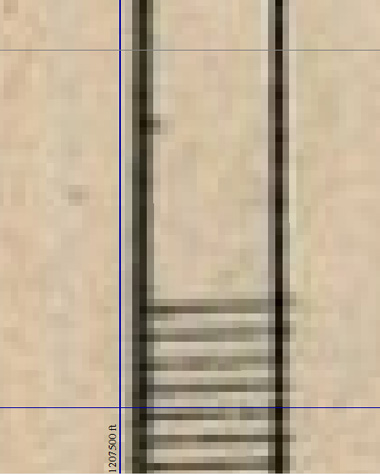
Здесь мы ограничимся иллюстрациями левого края карты; желающие могут убедиться, что и для правого края всё аналогично. Горизонтальная линия в 1459500 фута проходит практически по рамке, как и должно было бы быть, исходя из расчёта калькулятора:
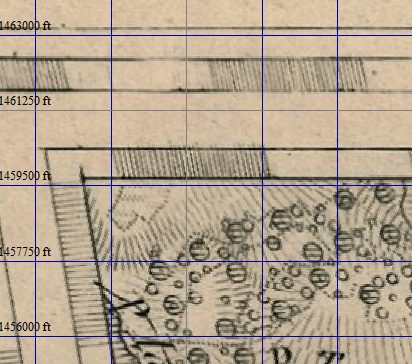
То же справедливо и для линии в 1286250 футов и нижней части рамки. Совпадения с вертикальными линиями сетки в углах рамки нет, поскольку она сильно скошена, однако, если внимательно рассмотреть область вблизи параллели, которую мы использовали для привязки, то можно увидеть, что вертикальная линия в 966000 футов пересекает край рамки как раз в районе этой параллели:
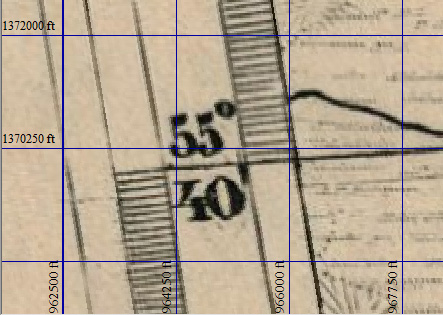
Это наблюдение является хорошей иллюстрацией того, что чем ближе к точке привязки мы находимся на области карты, тем точнее координаты окрестных точек. Вдали от точек привязки, а тем более в их отсутствие результаты будут совершенно неудовлетворительны.
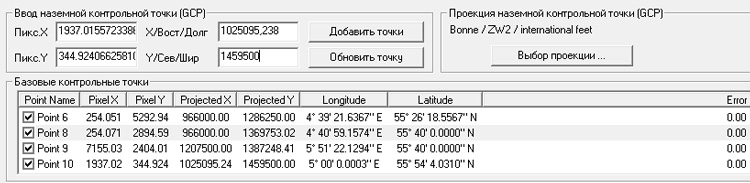
Для привязки карты по углам рамки наши действия будут похожими на предыдущие. Вновь откроем окно коррекции изображения, найдём нужный нам угол, увеличим изображение в центре окна и поставим точку:


В окно ввода контрольной точки записываем координаты точки в футах, полученные из калькулятора. Эти координаты проще копировать прямо из Excel:

После нажатия кнопки "Добавить точки" она немедленно появится в списке контрольных точек внизу окна. В данном случае формат координат целочисленный и Global Mapper дополнительных вопросов не задаёт, а правильно интерпретирует координаты, как линейные:

Обратим также внимание, что автоматически были рассчитаны и географические координаты точки. Точно таким же образом вводим линейные координаты трёх оставшихся точек - углов рамки, после чего нажатием кнопки "ОК" сохраняем привязку. Теперь результат значительно лучше предыдущего - растр выровнялся не только по горизонтали, но и по вертикали и приобрёл положенную ему прямоугольную форму:
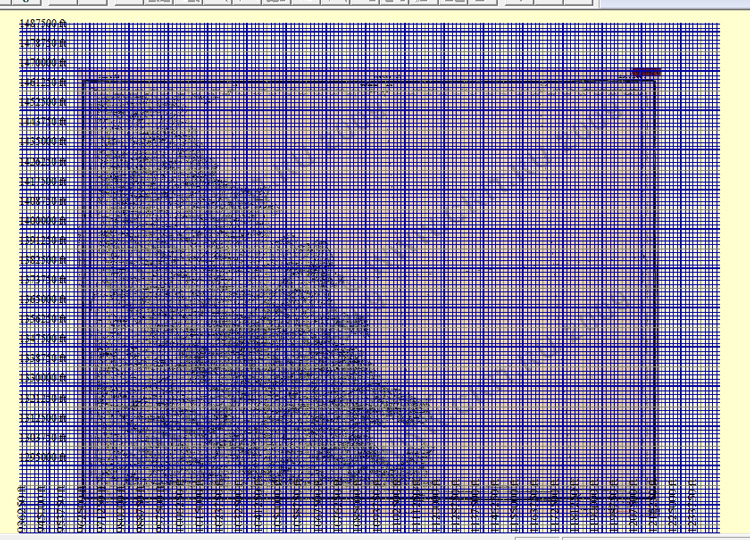
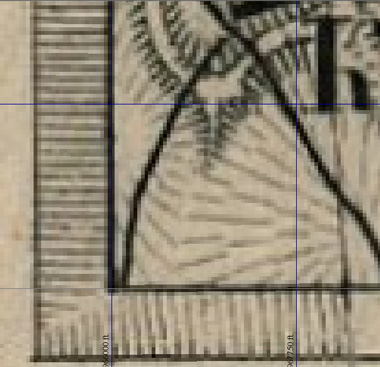
Теперь снова оценим нашу работу вблизи, увеличив карту до нужного масштаба. Видно, что углы рамки практически идеально совпадают с узлами полуверстовой сетки, небольшие отклонения наблюдаются лишь вдали от углов:
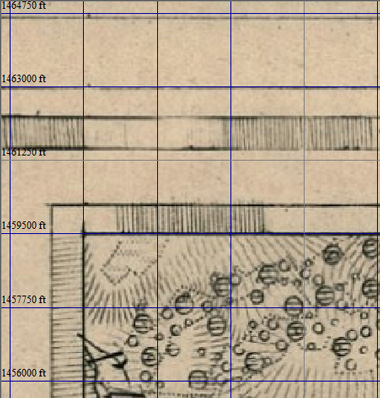
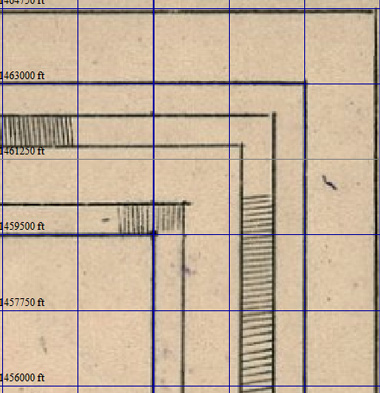
Чтобы лишний раз убелиться, что всё идёт нормально, временно переключим в окне конфигурации показ сетки на "Широта/долгота" и посмотрим совпадение линий координат карты с сеткой:
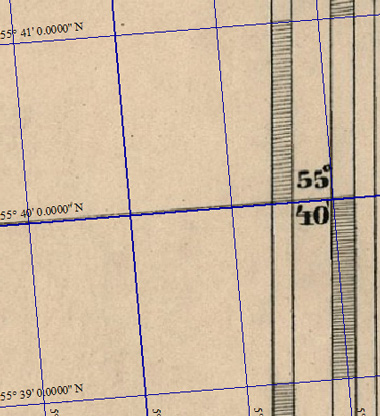
Небольшие отклонения наблюдаются лишь у левого края карты. Достаточно хорошо совпадают также линии долготы. Кстати, именно поэтому лучше использовать для привязки первоначальные настройки проекции с центральным меридианом "от Пулкова":
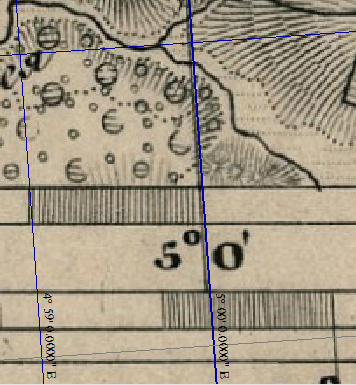
Все имеющиеся ещё погрешности мы уберём на следующем шаге, когда расставим дополнительные точки привязки по местам пересечения параллели и меридианов с рамкой карты.
Вначале займёмся параллелью. Вновь откроем калькулятор и в его части "Расчётные параметры проекции" введём значение широты для нашей изображённой на карте параллели:
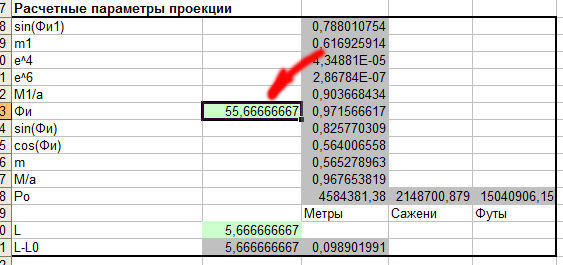
Ниже, в области расчёта пересечения параллели с рамкой введём абсциссу левого края рамки. Мы её знаем из предыдущего шага, когда рассчитывали координаты углов:
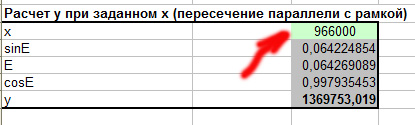
При этом мы немедленно получим ординату (значение y) точки пересечения. Нам останется найти точку пересечения в окне коррекции изображения, поставить точку привязки и в окошко ввода координат скопировать значение из Excel. Для примера здесь введены линейные координаты с десятичной запятой и Global Mapper автоматически правильно их интерпретирует, как линейные:
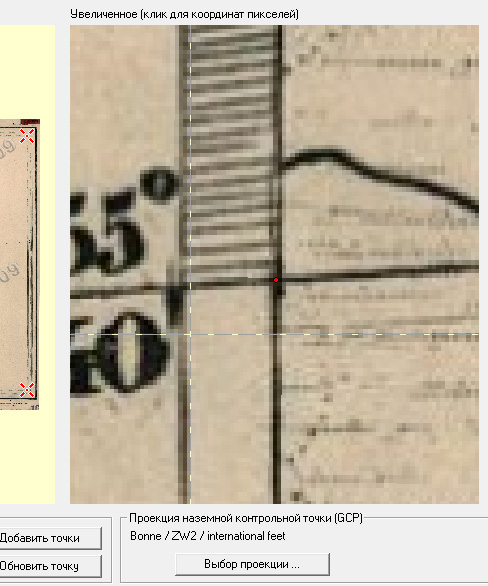


Ту же операцию повторим и для правого края рамки. Появление двух дополнительных точек привязки немедленно сказывается на качестве нашей работы:
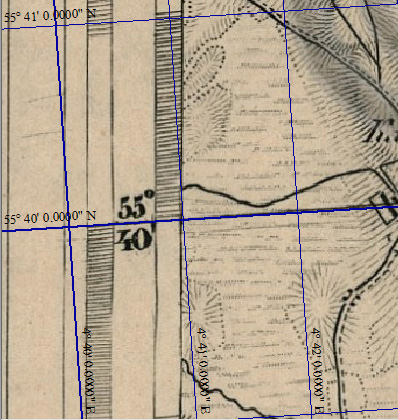
Параллель карты полностью совпадает с программной линией сетки, а отклонения линий меридианов нигде не превышают 3 пикселей, что, кстати говоря, уже укладывается в предельную точность масштаба карты. о которой говорилось выше. Но мы ещё улучшим привязку, рассчитав координаты точек пересечения меридианов с горизонтальными линиями рамки карты. Для такого расчёта вначале в части калькулятора "Расчётные параметры проекции" введем долготу пересечения:
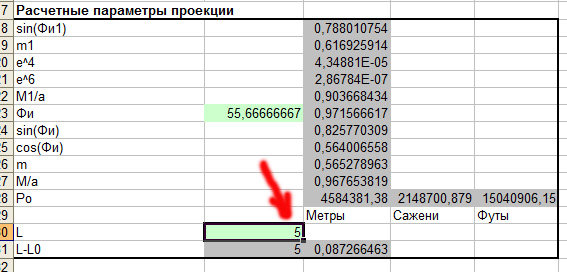
В части калькулятора, предназначенной для расчёта пересечения меридиана с рамкой для "заданного y" введём ординату, полученную нами при расчёте углов рамки, а для "пробного x" - любую величину из диапазона между левым и правым краями рамки:
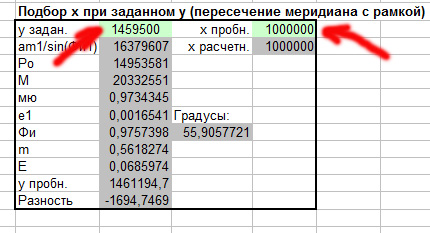
Запустив надстройку Excel "Поиск решения" мы получим необходимый нам результат:
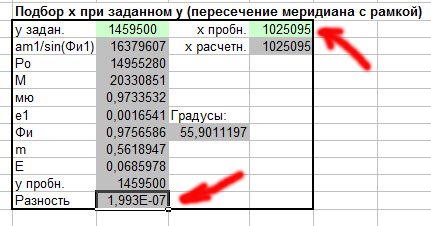
Нам останется найти место пересечения меридиана с рамкой карты в окне коррекции изображения, поставить точку привязки и ввести полученные координаты, то есть повторить все процедуры, описанные выше:

Описанный алгоритм (расчёт проекции - поиск решения - ввод контрольной точки) нужно повторить для каждой их оставшихся шести точек пересечения. В результате мы получим полностью привязанную по 16 точкам карту:
Оценить качество проделанной работы можно двумя способами: описанным выше визуальным контролем по линиям сетки (градусной или линейной) и математически. Ранее мы не трогали настройки метода расчёта привязанного растра программой. Поэтому, с учётом того, что у нас имеется 16 точек привязки, она автоматически выбирала триангуляционный метод восстановления и в колонке "Error" таблички контрольных точек стояли нули. Заменим его на полиномиальный метод восстановления (термин в русской версии программы неудачен, лучше называть его методом расчёта или пересчёта):
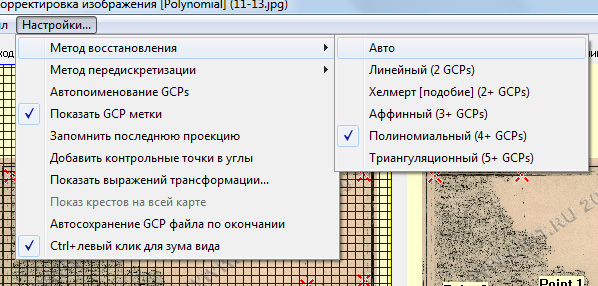
Мы увидим, что максимальная ошибка при таком методе расчёта составляет около 5 пикселей, а остальные не превышают 2-3 пикселей, что, как мы видели раньше, примерно и равно предельной точности масштаба карты:

Поэтому снова заменим метод расчёта на триангуляционный (поставим галочку на пункт "Авто") и снова визуально оценим нашу работу по сеткам. Мы увидим, что как для градусной, так и для линейной сеток, максимальное отклонение линии сетки от изображённой на карте не превышает 3-4 пикселей даже на самых "плохих" участках, которые максимально удалены от точек привязки. Вблизи же этих точек совпадение линий практически абсолютное:

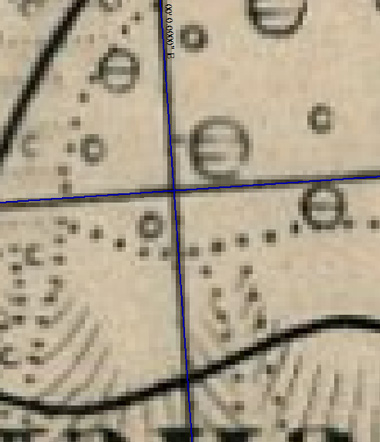
Ранее мы видели, что такая величина и соответствует нижней границе предельной точности масштаба карты, а это значит, что мы выполнили свою задачу в плане сохранения необходимой точности привязки. Теперь мы имеем полностью привязанную карту и, если бы мы с нашим программным обеспечением жили в XIX веке, то могли бы вполне ею пользоваться: координаты всех объектов на карте определяются именно в тех величинах, которые существовали в то время. Но сейчас мы используем другие, более современные системы координат и возникает вопрос: как же нам быть?
Для начала вспомним, что в качестве "ноля отсчёта" долготы мы использовали Пулковский меридиан. Сейчас значения долготы отсчитывают от Гринвича, поэтому нам нужно этот "ноль" изменить, при этом не нарушив привязку карты. Сразу скажу, что существует достаточно много значений разницы долгот между Пулковским и Гринвичским меридианами, в первую очередь, вследствие того, что со временем возрастала точность измерений. Современное значение этой разницы равно 30° 19′ 33.79″, но мы здесь и дальше будем брать величину в 30° 19' 38.31", поскольку именно эта величина по времени ее опубликования (в известном справочнике Ф.Ф. Шуберта) наиболее близка ко времени создания карт. Так что, методически, значения долгот, которые получатся при использовании второй величины будут ближе к значениям, которые получились бы в XIX веке, если бы на картах использовался отсчёт "от Гринвича". В конце концов, разница в 4,5" или примерно в 80 метров - это лишь поворот земного эллипсоида ровно на эту величину и, в любом случае, будет скомпенсирована при расчёте датума, о чём речь пойдет немного ниже.
Чтобы сделать все наши значения долготы "гринвичскими", вновь откроем окно коррекции/привязки изображения, а в нём - нажмём кнопку "Выбор проекции". Теперь для центрального меридиана вместо нулевого значения введём значение 30,32730833 (в десятичных градусах):
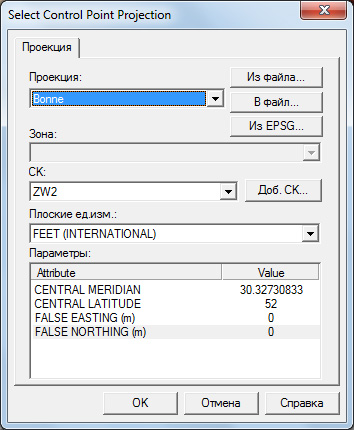
После нажатия кнопки "ОК" программа задаст уточняющий, но не очень понятный вопрос:
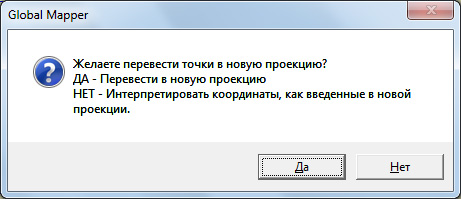
На него следует ответить "Нет", так как вопрос относится именно к прямоугольным координатам, вне зависимости от того, в каком виде, градусном или линейном мы вводили точки привязки. Эти координаты нам и не нужно менять. И тогда в новой проекции пересчитаются все координаты в градусах:
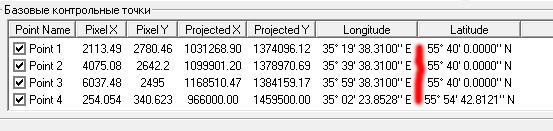
Понятно, что пересчитаются только долготы, широты останутся неизменными. Это значит, что теперь линии долготы нашей сетки уже не будут совпадать с линиями, изображёнными на карте (так как введённая нами разница нецелая). Но линии параллелей по-прежнему будут совпадать:
Кроме того, будут совпадать с углами карты и линии нащей полуверстовой сетки, поскольку преобразование координат их не затронуло.
Теперь наша карта имеет координаты вподне современного вида. Однако, пользоваться ей ещё нельзя, поскольку она привязана в другой системе координат, нежели используемые в наши дни. Говоря совсем просто, разница в том, что карта изображена на одном эллипсоиде, а современная местность лежит на другом, и эти эллипсоиды во-первых, не равны по размерам, а во-вторых смещены друг относительно друга. Поэтому, для того, чтобы карта в точности совпала с местностью, эти эллипсоиды нужно совместить, хотя бы приблизительно. Именно этим целям и служат те параметры системы координат, которые в самом начале нашей работы, на первом шаге мы посчитали нулевыми. Теперь настало время их вычислить. Сразу скажу, что для более точного преобразования используют 7 параметров: по 3 параметра сдвига по осям координат, по 3 угла поворота эллипсоида вокруг осей координат и параметр масштабирования. Однако, определение всех этих параметров с приемлемой точностью возможно лишь с использованием достаточно большого массива точек. Кроме того, эти точки должны достаточно далеко располагаться одна от другой на местности, размеров одного листа карты для этого недостаточно. Поэтому мы воспользуемся упрощённым вариантом расчёта и будем использовать лишь 3 параметра (сдвиги по осям координат). Нужно только иметь в виду, что эти параметры могут получаться каждый раз разными для разных листов трёхвёрсток, особенно для тех, которые находятся далеко друг от друга. Семипараметрическое преобразование даёт гораздо более "общий" результат, который подходит для обширных участков местности (таких, как общее покрытие трёхвёрстных карт), но такой расчёт выходит за рамки этой статьи.
Шаг шестой.
Итак, алгоритм действий будет следующим: вначале нужно определить те объекты на карте, современные координаты (в СК WGS84) которых известны и измерены с достаточной точностью, измерить эти координаты на привязанной нами карте и, наконец, имея два набора координат, с помощью специальных программ рассчитать параметры искомой СК. Самыми известными такими программами являются Inverse Molodensky для вычисления трёхпараметрического преобразования и более продвинутая, но, к сожалению, платная Sevenpar, в которой возможен расчёт как трёх-, так и семипараметрического преобразования. Серьёзным недостатком первой программы является то, что для расчёта можно использовать не более трёх точек - абсолютный минимум для вычисления трёх параметров. У второй программы такого ограничения нет, и следовательно, возможна статистическая обработка результатов и вычисление погрешностей расчёта.
Какие же объекты нам следует взять для дальнейших расчётов? Из рассмотрения следует сразу же исключить перекрёстки дорог (они не раз перепрокладывались, даже внутри населённых пунктов), мосты (обычно новый мост строится не на месте старого, а рядом, чтобы не прерывать дорожного сообщения), мельницы и прочие мелкие объекты (они, в подавляющем большинстве своём не сохранились). Остаются лишь здания церквей. Они достаточно компактны, чтобы можно было считать их точечными объектами, но мы должны помнить непременные условия: церковь должна сохраниться до наших дней, быть построенной как минимум раньше создания листа карты и, самое главное, не должна заметно перестраиваться. Что касается нашего листа, то такие объекты на нём есть, а современные координаты их можно получить тремя способами. Первый способ - самый простой, но самый неточный и ненадёжный: "считать" их с современной карты. Причины неточности понятны: возможные ошибки на карте плюс ограничения масштаба. Способ второй - воспользоваться онлайновыми базами данных этих объектов. Для этих целей хороши два сайта: http://sobory.ru/ и http://temples.ru/, но, к сожалению, координаты нужного объекта там не всегда есть. Поэтому лучше всего, если есть такая возможность, определить координаты самому, "на местности", и только если это невозможно, воспользоваться вторым или даже первым способом. Способ более или менее точного определения координат выходит за рамки этой статьи, здесь лишь скажу о том, что измерять координаты следует с точностью не меньшей предельной точности масштаба нашей карты. Лучше всего, если погрешность не превысит 3 метров, в качестве измеряемого объекта по возможности следует брать геометрический центр колокольни церкви (если таковая есть), поскольку именно колокольни использовались в большинстве случаев для определения координат в XIX веке (в этом можно убедиться, заглянув в упомянутый выше справочник Шуберта).
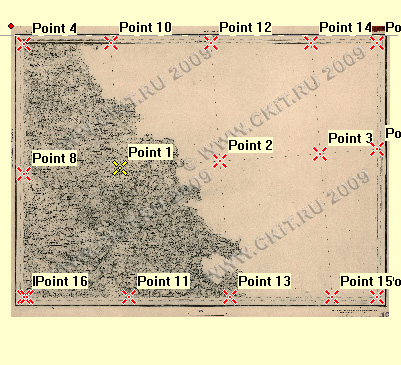
На нашем листе имеется всего три подходящих под нужные критерии объекта: это церкви в Дровнино, Новопокрове (Покров на карте) и в Мокром. Они обозначены на карте ниже зелёными точками. Есть ещё два собора в самом Гжатске, но один из них во время войны утратил колокольню, а второй - имеет датой постройки начало XX века. Правда, утверждается, что будто бы на месте более старого храма, но так обычно говорят о любой церкви. Эти две точки отмечены красным цветом. Остальные объекты либо полностью уничтожены, либо ныне представляют собой откровенный "новодел", построенный вовсе не на месте старых церквей.
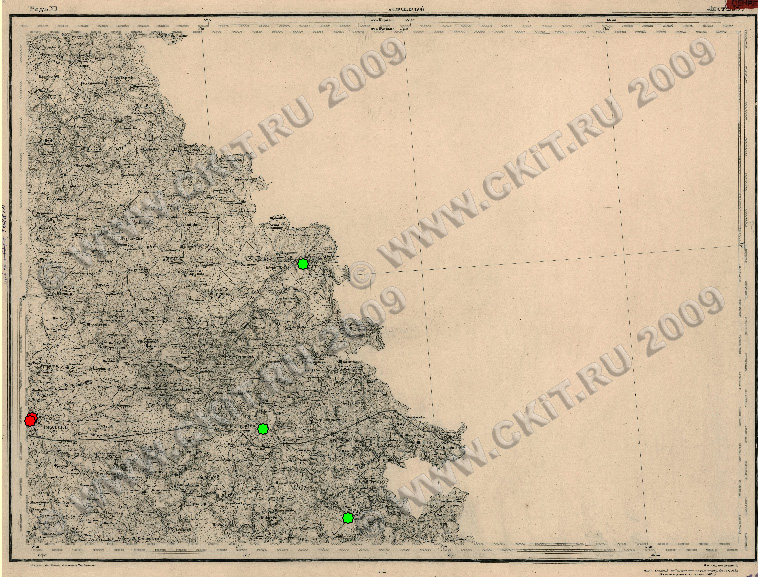
Видно, что расположение объектов, пригодных для расчёта, крайне неудачно: все они сгруппировались в юго-западной четверти карты, включая сомнительные, хотя, всё же, и достаточно далеко друг от друга. Северная часть вообще осталась без пригодных точек, да и сам лист содержит меньше половины площади информативного материала. Так часто бывает; приходится стараться и извлекать максимум пользы из ограниченных данных и пробовать разные варианты решения, чем мы и займёмся на следующем шаге.
Шаг седьмой.
Наконец, настаёт последний этап привязки: вычисление скорректированной системы координат (датума). Для этого нам нужно получить два набора точек: координаты в WGS84 и координаты на нашей карте. Что касается первого набора, то он был получен самым надёжным способом - полевой работой на местности. Остаётся определить второй набор.
Найдём на листе карты нужную точку и максимально увеличим масштаб:
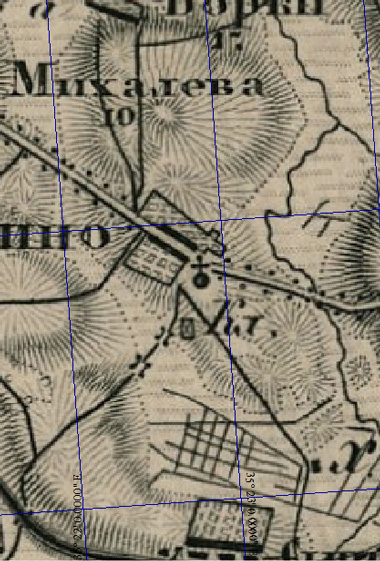

Теперь включим инструмент "Дигитайзер" и поставим точку примерно посередине значка нашей первой церкви. Координаты её можно прочитать внизу окна программы в строке состояния, а можно включить инструмент "Информация" и, щёлкнув по точке, открыть окно, в котором эти координаты будут содержаться:
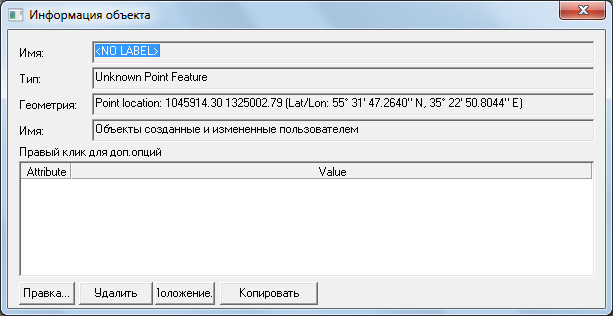
Полученные координаты перенесём в табличку. Она устроена по принципу простейшего координатного калькулятора. Дело в том, что чуть позже нам придётся использовать координаты в разных форматах: в секундах и в градусах с десятичной запятой, поэтому об удобстве работы следует позаботиться заранее:

В этой табличке мы будем не только хранить расчётные точки, она даст нам возможность сразу получать координаты в самых разных единицах. Занесём в неё координаты всех пяти обнаруженных нами на карте точек. Но прежде, чем заниматься расчётами стоит посмотреть, как до исправления датума наша карта соотносится с реальным миром. Для этого загрузим на неё треки, полученные при движении по реальной местности:
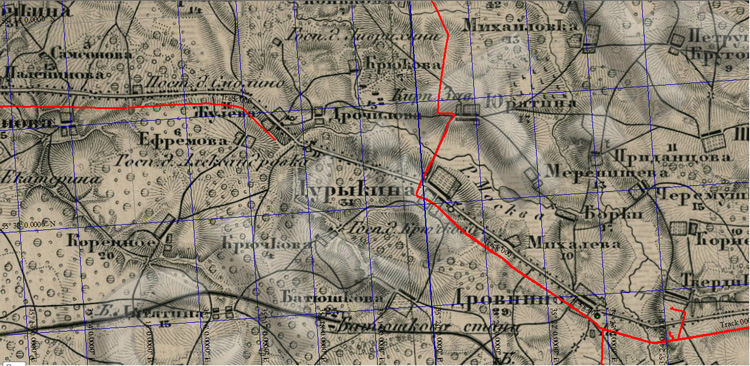
Видно, что хотя и есть определённое соответствие, карта выглядит сдвинутой на величину некоторой постоянной погрешности, метров примерно в 300. Её нам и предстоит, по возможности, исправить, а пока сохраним рабочее пространство программы.
Вначале для расчёта попробуем программу Inverse Molodensky. Как ею пользоваться вполне понятно из рисунка. Параметры целевой системы координат (WGS84) в ней уже содержатся, нам нужно ввести в неё параметры эллипсоида Вальбека и три пары координат - координаты в WGS84, полученные "полевыми" измерениями и координаты в нашей системе ZW2 с привязанной карты. В качестве пробных точек возьмём те, в измерении координат которых мы не сомневаемся (ранее мы их обозначили зелёным цветом). Координаты следует вводить в секундах:
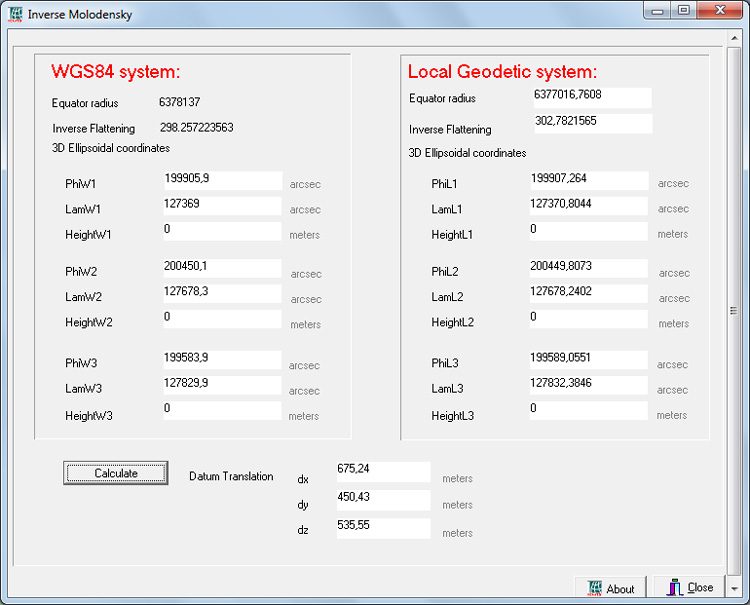
Для более точного расчёта, конечно же, было бы неплохо знать и высоты точек, более того, мы могли бы их измерить и на местности, но проблема в том, что для нашей карты они неизвестны. Поэтому в окошках с высотами проставим везде нули. Тем самым будем считать, что и реальная местность, и местность, изображённая на карте лежит строго на поверхности эллипсоида. Далее, нажав кнопку "Calculate" немедленно получим поправки для системы координат.
Теперь, чтобы убедиться, что обе программы дают сходные результаты, загрузим этот же набор точек в Sevenpar. При этом в программе выставим соответствующие настройки: запишем параметры нашего эллипсоида для СК источника (встроенного эллипсоида Вальбека в программе нет), выберем для целевой СК "WGS84", установим нужный формат ввода координат (десятичные градусы без значений высоты) и необходимое преобразование (в нашем случае, преобразование Молоденского). После чего в верхние окна введем значения координат в градусах с десятичной точкой). Нажав кнопку "Calculate transformation parameters", убедимся, что программа даёт практически идентичный предыдущему результат (с точностью до ошибки вычислений):
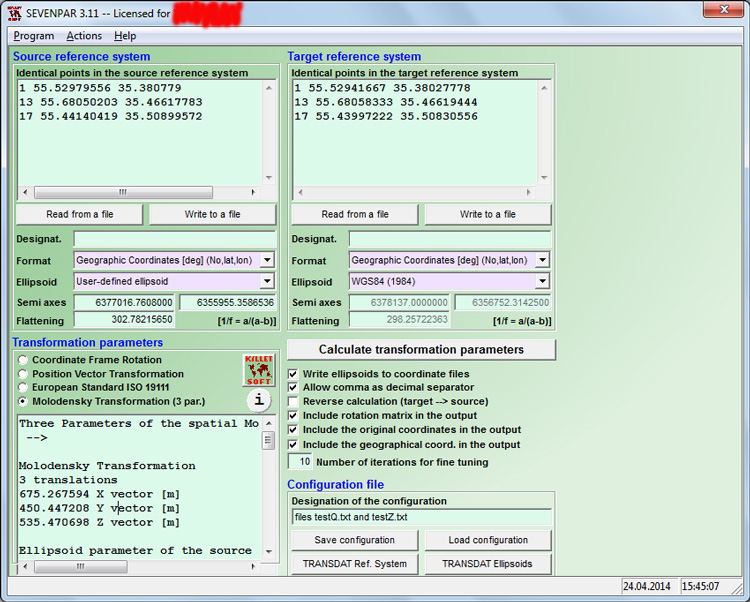
Важных преимуществ программы Sevenpar перед Inverse Molodensky два: она позволяет вводить для расчёта неограниченное количество точек и позволяет провести статистическую обработку результатов. Фактически, для найденного наилучшего решения программа оценивает, насколько ей удалось приблизить набор точек, заданных в одной СК к набору точек в другой. Программа делает такой расчёт как для каждой пары точек, так и вычисляет средние для всего набора:
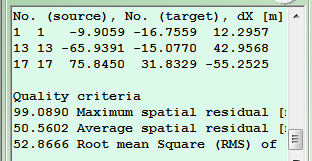
Из полученных данных видно, что максимальный пространственный остаток в 99 метров получился для третьей точки (это церковь в Мокром), что лишь немного превышает верхнюю границу нашей оценки предельной точности масштаба карты. В то же время, средний остаток равен примерно 50 метрам, что в эту оценку вполне укладывается.
Попробуем теперь поэкспериментировать и посмотрим, не сможем ли мы улучшить результат, взяв ещё две дополнительные точки (те, которые отмечены были нами красным цветом, как вызывающие определённые сомнения). Добавим их к списку и проведём повторный расчёт (в списке это точки с номерами 5 и 6):
Residuals between the coordinates of the source and target reference systems
No. (source), No. (target), dX [m], dY [m], dZ[m]
1 1 12.9401 54.8499 -28.7225
5 5 -63.5007 -64.8029 61.1896
6 6 -5.0374 -150.0144 61.8649
13 13 -43.0930 56.5288 1.9386
17 17 98.6911 103.4386 -96.2706
Quality criteria
172.3587 Maximum spatial residual [m]
96.4170 Average spatial residual [m]
80.1549 Root mean Square (RMS) of residuals [m]
Видим, что средний остаток вырос, в первую очередь из-за 6 точки (та самая церковь без колокольни в Гжатске), её отклонение по одной из осей составило больше 150 метров, что уже сильно превышает предельную точность масштаба. Попробуем от неё избавиться и провести расчёт по 4 точкам:
Residuals between the coordinates of the source and target reference systems
No. (source), No. (target), dX [m], dY [m], dZ[m]
1 1 11.6808 17.3463 -13.2563
5 5 -64.7601 -102.3065 76.6559
13 13 -44.3524 19.0252 17.4048
17 17 97.4317 65.9350 -80.8044
Quality criteria
143.3060 Maximum spatial residual [m]
72.4184 Average spatial residual [m]
70.0408 Root mean Square (RMS) of residuals [m]
Средний остаток немного уменьшился, но всё равно больше, чем при расчёте по трём надёжным точкам. Теперь сильно выпадает точка номер 5 - тот самый собор, построенный "на месте более старого". Ну что же, нам остаётся забраковать и эту точку и вернуться к самому первому решению, использующему три точки. Оно и есть наиболее точное и надёжное. Нам останется только создать новую систему координат, которая будет использовать именно эти параметры.
Для этого вновь откроем файл custom_datums.txt, который мы создали на первом шаге и добавим в него строчку примерного вида:
"CW21113","CW21113","Walbeck 1819 (2)",675.27000000000000000, 450.45000000000000000,535.47000000000000000
В обозначение системы координат мы добавили номенклатурное обозначение листа карты, поскольку, вообще говоря, расчёт параметров датума пока справедлив только для него из-за недостатка других данных. Сохраним файл и запустим Global Mapper. Вновь откроем окно корректировки изображения и нажмём кнопку "Выбор проекции". В открывшемся диалоге выбора проекции заменим систему координат на новую и нажмём кнопку "ОК":
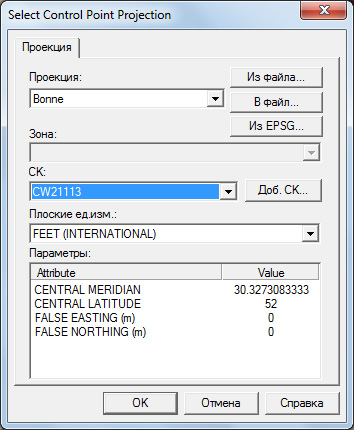
Программа вновь задаст нам вопрос, как ей интерпретировать введённые точки. Поскольку нам необходимо сохранить линейные координаты в неизменном виде, вновь ответим на этот вопрос "Нет". Поскольку и никаких параметров проекции, кроме замены СК, мы не меняли, то останутся неизменными не только координаты проекции, но и географические координаты:

Выйдем из окна коррекции и посмотрим, что у нас получилось. Сразу же становится видно, насколько точнее ложатся треки на те участки дорог, о которых известно, что они практически не изменили положение до нынешнего времени:
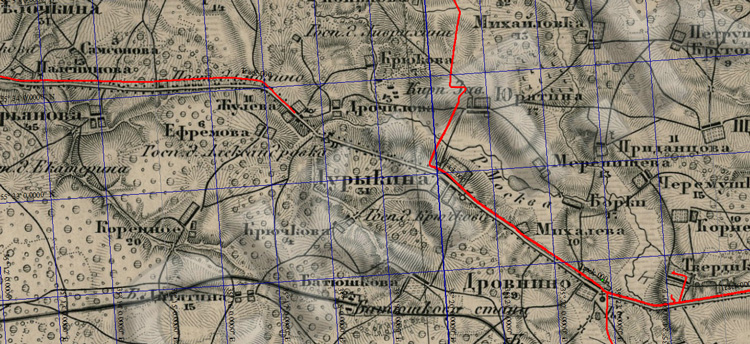
Наконец, прежде чем посчитать нашу привязку в Global Mapper окончательно завершённой, посмотрим вблизи, что у нас произошло с теми точками, по которым мы осуществляли коррекцию СК. На увеличенных фрагментах карты зелёные точки - это первоначальное расположение объектов до сдвига, мы их старались ставить по центру объекта. По ним можно оценить величину и направление сдвига карты в результате пересчёта СК. А оранжевым обозначены реальные точки, полученные в результате "полевых" измерений, которые мы использовали в расчёте:



Хорошо видно, что отклонения соответствуют тем оценкам, которые нам сделала программа Sevenpar и лежат в диапазоне от 20 до 90 метров, а в среднем - 50-60 метров. Как мы помним, эти величины соответствуют "вилке" оценки предельной точности масштаба карты, данной нами на третьем шаге. К сожалению, большую точность на этом наборе точек получить нельзя, поскольку пока мы не можем воспользоваться возможностями семипараметрического преобразования. Но и этой точности в большинстве случаев хватит, чуть раньше мы уже увидели, что отклонения объектов карты от их реального местоположения составляет всего лишь несколько пикселей, то есть несколько десятков метров. Более же точные вычисления будут предметом нашей следующей статьи, где мы обработаем больший массив карт и точек коррекции. Сейчас же ещё раз подчеркнём тот факт, что при таком подходе ни градусная, ни линейная сетки новой проекции не изменили своего расположения и в точности соответствуют сетке координат и рамке привязанной карты.
(Окончание следует)
Вы можете поблагодарить автора этой статьи, например, здесь.