«Параллель Тучкова». Часть десятая, в которой находятся ответы на все оставшиеся вопросы. Кроме одного

Давайте теперь обратимся к тем частям нашего рассказа, которые мы либо оставили совсем без рассмотрения «на будущее», либо, получив предварительный результат, не смогли окончательно его оформить из-за ограничений возможностей статистических расчетов в офисных пакетах, которые мы с вами использовали ранее. Теперь же, с использованием языка R, мы ответим и на все эти оставшиеся вопросы.

ВЛИЯНИЕ КОЛИЧЕСТВА ИЗМЕРЕНИЙ

Начнем с количества экспериментальных точек (измерений), которые нам понадобятся для определения искомого параметра нелинейной регрессии (широты главной параллели) и которых будет достаточно для работы с приемлемой точностью. Как вы помните, в предыдущей части мы с вами использовали весь массив данных — 160 измерений. Это, конечно, много и сбор такого количества данных довольно трудоемок. Впрочем, ранее уже было показано, что для определения параметра, значение которого получается довольно близким к значению, полученному на всем массиве, достаточно десяти или даже пяти измерений. Однако за кадром остался вопрос: а с какой точностью мы с вами получаем это «довольно близкое значение»? Внимательный читатель, конечно же, помнит, что именно с вопросом оценки доверительных интервалов в нашем частном случае нелинейной регрессии офисные пакеты не справляются [1].

Давайте тогда посмотрим, насколько легко такая задача решается средствами языка R. Начнем с получения исходных данных — случайной выборки некоторого количества измерений (например, десяти) из общего массива [2]. Как вы помните, раньше для такого извлечения нам с вами пришлось добавить в исходную таблицу с данными дополнительный столбец со случайными числами и пересортировать таблицу по этому столбцу. В R же такая задача решается буквально одной строчкой кода и такая команда приведена на рисунке ниже. В ней записано буквально следующее: из всего количества данных нашего исходного тиббла TP нужно выбрать только те, которые удовлетворяют некоторым условиям x и y: TP[x,y] (квадратные скобки указывают на индексацию этих данных внутри исходного тиббла в виде указаний на строку x и столбец y). Вместо x (номера строки) у нас стоит некоторое выражение, а вместо y (номера столбца) — просто пробел перед закрывающей квадратной скобкой, и это означает, что надо выбрать все столбцы. Само же выражение для x (номеров строк) представляет собой функцию sample(), которая и занимается случайной выборкой из всего набора данных (а внутри этой функции мы указываем ей, что нужно из всего количества строк в тиббле nrow() выбрать 10). Выбранные таким образом строки поместим вновь в переменную TP [3].

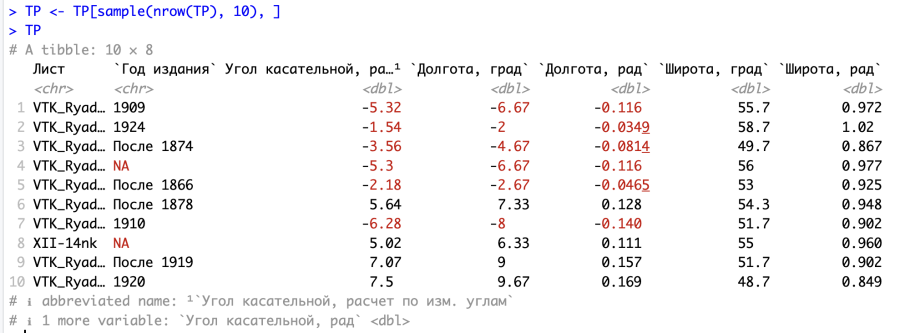
Видим, что теперь наша переменная TP представляет собой другой тиббл, где количество и названия столбцов остались такими же, как и в исходном тиббле, а вот количество строк изменилось со 160 до 10, причем выбрались они в случайном порядке.

Теперь подготовим данные для расчета регрессии. Здесь мы поступим в точности так же, как и в предыдущей части: создадим три переменных-вектора E_dg, fi_dg и lambda_dg (понятно, что каждый такой вектор будет содержать не 160, а лишь 10 значений).

Теперь мы с вами можем использовать эти новые переменные для нового расчета регрессии — но точно так же, как мы рассчитывали ее по полному массиву точек.

И вновь за 6 итераций расчет сошелся к значению параметра, близкому к 52°. Впрочем, команда summary() покажет нам, что стандартная ошибка подросла с 0.1 до примерно 0.3. Так и должно быть, ведь мы пожертвовали точностью вычислений в пользу существенного уменьшения необходимых нам данных.

Здесь нам остается вывести остатки регрессии (снова сделаем это в минутах) и посчитать новые доверительные интервалы для полученного параметра широты (сделаем это так же в двух вариантах: для уровня 95% и для уровня в 99%).

Видим, что даже для «широкого» 99%-ного доверительного интервала значение широты главной параллели лежат в диапазоне 51.7±1.1°. Если же немного снизить надежность утверждения до 95%, то наша широта уложится в диапазон 51.7±0.8°, и для этого нам с вами хватило всего 10 измерений!

Давайте теперь проведем более экстремальный расчет и ограничимся всего пятью точками-измерениями. Поскольку переменную TP мы изменили командой выше, перечитаем ее заново из файла TP.rds.

Снова совершим операцию выборки, но в этот раз выберем лишь 5 случайных строк.

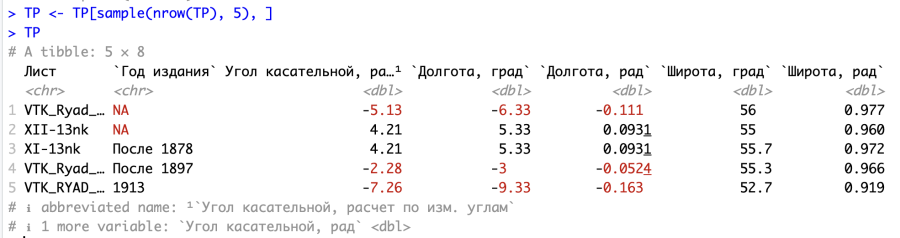
Переприсвоим значения переменным-векторам E_dg, fi_dg и lambda_dg (теперь они будут содержать лишь по 5 значений) и вновь запустим процедуру нелинейной регрессии.

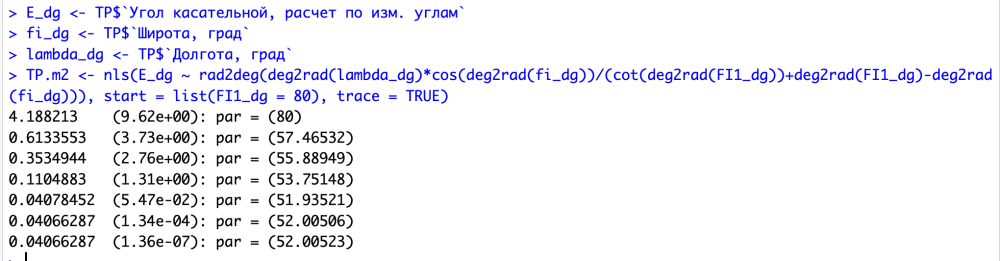
В этот раз значение параметра получилось даже ближе к 52°, чем в случае расчета по 10 точкам! Однако можно заметить, что подросла и его стандартная ошибка (0.6 против 0.3 для случая с 10 измерениями и 0.1 для полного массива из 160 точек).

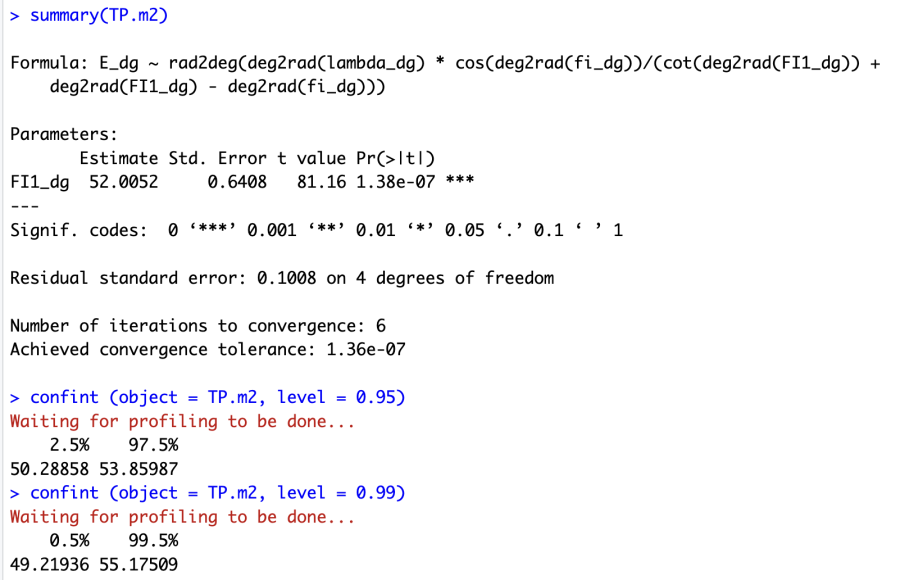
Нам с вами останется лишь подсчитать новые доверительные интервалы для этой выборки из 5 точек. Можно видеть, что для 95%-ного доверительного интервала значения параметра лежат в диапазоне 52±1.9°, а вот для 99%-ного — в диапазоне 52±3.1°, тем самым захватывая самым краешком интервала и значение в 55° [4]. Таким образом, можно сделать вывод о том, что хотя мы с вами можем получить значение широты главной параллели и на минимальном количестве измерений, более или менее приемлемая точность достигается при количестве измерений ближе к 10 (или выше). Кроме того, слишком малое количество таких измерений не позволяет нам полностью исключить вероятность (хотя и малую) того, что широта главной параллели может иметь значение и в 55°. Немного ниже мы с вами займемся подробнее и этим вопросом.

АНАЛИЗ ОСТАТКОВ

Обратимся теперь к еще одному важному вопросу: о нормальности распределения остатков регрессии. Известно, что нормальное распределение остатков является одним из важных требований верности модели линейной или нелинейной регрессии [5]. Впрочем, также хорошо известно, что для нелинейной регрессии нормальность остатков часто нарушается [6], а с другой стороны, небольшие отклонения от нормальности мало сказываются на конечных результатах вычислений [7].

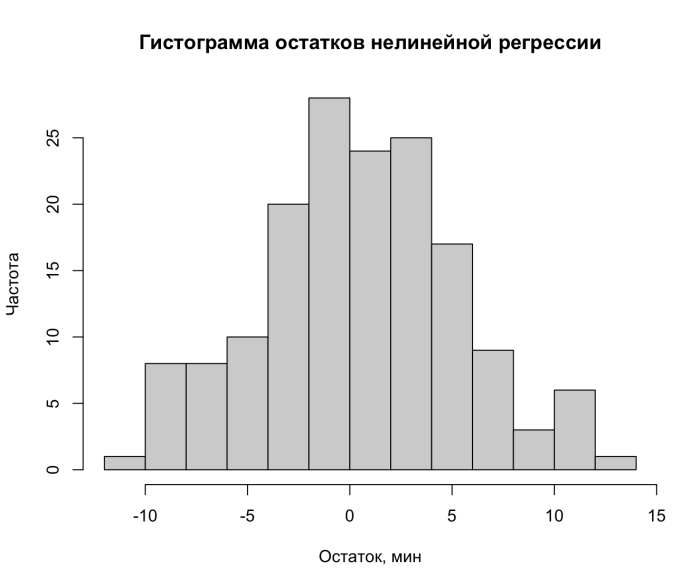
Воспроизведем еще раз нашу гистограмму остатков нелинейной регрессии по всему массиву из 160 измерений, которую мы с вами видели в восьмой части [8]. Для этого служит команда R hist(), которую следует применить к вектору остатков [9].

Ранее мы с вами остановились на том, что она выглядит вполне похожей на нормальное распределение, и не вдавались в дальнейшие подробности. Теперь пришло время дать и некоторые количественные характеристики этого утверждения.

Полностью текст статьи вы можете прочитать, посетив страницу автора на Boosty.