«Параллель Тучкова». Часть восьмая, в которой один из экспертов впервые терпит полное фиаско

О неудачах всегда довольно трудно рассказывать. Ведь, на первый взгляд, ничего нового для продвижения к поставленной цели неудачи не добавляют. И несмотря на расхожую фразу «отрицательный результат — тоже результат», об «отрицательных результатах» не очень принято говорить и в научной литературе, особенно посвященной статистическим методам. В самом деле, почти всегда считается, что получить значимую зависимость или узкий доверительный интервал для параметра интереснее, чем не получить вообще ничего.

Однако мне показалось важным опубликовать результаты, изложенные ниже, с одной целью: показать, как неверный подход к использованию формальных статистических методов может критически сказаться на полученных результатах и, в конечном итоге, привести к совершенно бесполезным выводам. Кроме того, здесь я еще коснусь тех «подводных камней», существование которых было намечено в предыдущих главах.

Поскольку мы с вами теперь вплотную займемся оценками точности рассчитываемого параметра (широты главной параллели), то в этой части речь пойдет об одной из попыток решить задачу простым способом: с помощью линеаризации нашей модели. Линеаризация модели — это способ сведения задачи нелинейной регрессии к решению задачи регрессии линейной с помощью некоторых алгебраических преобразований исходной модели.

Из теории регрессионного анализа известно [1], что в общем случае при линеаризации оценки параметров регрессии и их доверительных интервалов могут получиться смещенными [2], однако если мы будем об этом помнить, никто не мешает использовать такие оценки как грубые приближения искомых величин (тем не менее, как мы с вами увидим ниже, оценка степени такой грубости нам и не понадобится). Впрочем, этот недостаток (смещенность оценки) вполне компенсируется простотой расчетов, а также их доступностью: ведь инструмент «Линейная регрессиия» включен в состав практически любого офисного пакета, работающего с электронными таблицами, в том числе и программы Calc пакета LibreOffice, которую мы с успехом использовали на предыдущих этапах. А самое главное, этот инструмент позволяет рассчитать описательную статистику регрессии, включая доверительные интервалы параметров: это то, чего сильно не хватает во встроенных инструментах нелинейной регрессии в офисных пакетах.

Итак, займемся линеаризацией. Преобразовывать будем формулы для сферы, поскольку как было показано ранее, никакого влияния на результат расчета усложнение модели (на сфероиде) не оказывает [3]. Снова выпишем нашу формулу для угла наклона касательной:

E = λ*cosφ/(ctgφ(1) + φ(1) - φ)  (2*)

Обозначим y = 1/E и A = ctgφ(1) + φ(1). Тогда получим:

y = (A - φ) / λ*cosφ

Перейдем к новым переменным z1 = 1 / λ*cosφ и z2 = φ / λ*cosφ. Окончательно получим:

y = A*z1 - z2 (9)

Видно, что у нас получилось линейное уравнение относительно переменных z1 и z2 и его можно решить методом линейной регрессии. Можно было бы... если бы не несколько «но».

Первое. При постоянном значении широты φ (а как мы с вами помним из предыдущих частей, такие данные у нас часто встречаются) переменные z1 и z2 получаются связанными линейной зависимостью. Влияние этого факта мы увидим при дальнейшем изложении.

Второе намного хуже. Дело в том, что стандартные офисные программы, в которые входит инструмент линейной регрессии (наш Calc или Excel), умеют решать задачи линейной регрессии лишь для общей формулы вида y = A*z1 + B*z2 + C. В нашем же случае коэффициент B по определению получился жестко фиксированным и равным -1. Такой вариант линейной регрессии также хорошо известен и называется «линейной регрессией с ограничением по параметру», однако именно такую задачу стандартные программы решать не умеют. Максимум, на что они способны — это ограничение C = 0, что также необходимо в формуле (9).

Ну что ж. Тем не менее, давайте посмотрим, что же у нас получится, если мы с вами пренебрежем этими фактами. Вначале еще раз обработаем исходные данные. Скопируем их на новый лист — «Линеаризация на сфере». Последние расчетные столбцы с промежуточными расчетами по нелинейному уравнению и с ошибками нам теперь не понадобятся, поскольку инструмент линейной регрессии посчитает их за нас. Нужны же нам будут только расчет новых переменных z1 и z2 и величина y (обратная функция угла наклона E). 

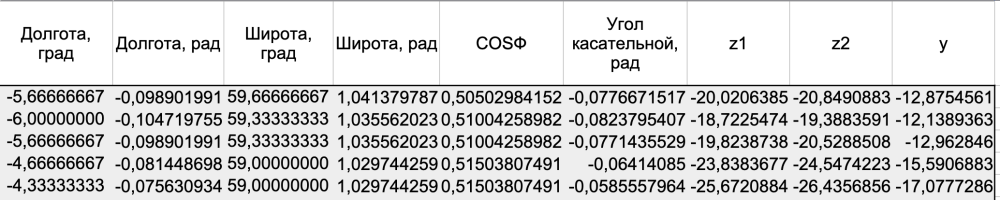
Стоит сразу обратить внимание, что в парах новых переменных z1 и z2 получились довольно близкие значения. Но это внешнее впечатление, давайте посмотрим, как они будут выглядеть на графике, аналогичном тому, который мы с вами строили в пятой части для координат «широта-долгота».

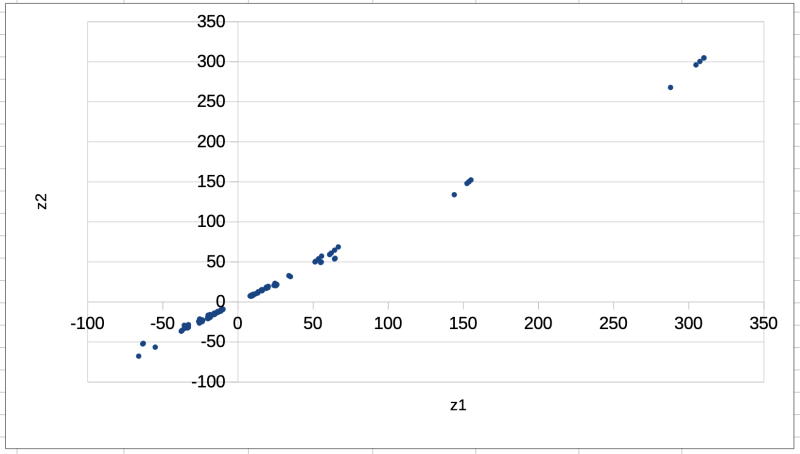
Полностью текст статьи вы можете прочитать, посетив страницу автора на Boosty.