Загадка «проекции Мюфлинга»: работа над ошибками
В 2016 году в журнале "Россия 4D" вышла статья "Загадка проекции Мюфлинга". В ней был предложен оригинальный метод перепроецирования крупномасштабных карт первой трети XX века, составленных в неудобной для современного использования многогранной проекции в более подходящую проекцию.
Коротко напомню, о чем шла речь.
Листы карт в проекции Мюфлинга представляют собой симметричные трапеции, ограниченные по рамке параллелями и меридианами, взятыми с равным шагом и изображенными прямыми линиями. Тем самым они представляют криволинейные трапеции на земной поверхности, преобразованные в трапеции на плоскости проецированием. Однако хорошо известно, что такое представление не позволяет отобразить земную поверхность на плоскости без разрывов между листами. В то же время, листы крупномасштабных карт (например, двухверстного масштаба) имеют крайне незначительный наклон боковых сторон трапеции (обусловленный схождением меридианов к северу) и представляют собой "почти прямоугольник". Поэтому и было предложено перепроецировать эти карты одновременно с привязкой в подходящую прямоугольную (цилиндрическую) проекцию, которая уже позволит собрать листы карт в единое покрытие без разрывов. Современные ГИС легко справляются с такой задачей.
В качестве такой проекции было предложено использовать проекцию Меркатора. Однако здесь есть один подводный камень, который я упустил в своих рассуждениях.
В самом деле, отклонение трапеции карты от "честной прямоугольности" составляет всего лишь пару миллиметров, поэтому представляется довольно простой задачей слегка подтянув отсканированный растр, подогнать ее к прямоугольнику. Но тут-то и таится допущенный пробел в рассуждениях: нам надо рассматривать растяжение трапеции в прямоугольник не только по горизонтали (верхней стороны), но и по вертикали (всей трапеции как целого)! И дело здесь не в величине самого растяжения (я подробней эту величину рассмотрю ниже), а в том, что такая операция не учитывает одного важнейшего свойства меркаторской проекции. Рассмотрим подробней, о чем идет речь.
Хорошо известно, что сетка параллелей и меридианов в проекции Меркатора вытягивается в вертикальном направлении при движении от экватора к полюсам. То есть, при равной ширине, любой прямоугольник, ограниченный фиксированным шагом широты и долготы становится более вытянутым по вертикали. Менее очевидным, но вполне объективным, является тот факт, что такое поведение характерно для любого участка заданного прямоугольника: масштабный коэффициент по вертикали нарастает при движении с юга на север (в Северном полушарии). Еще менее очевидно, что точно так же нарастает и масштабный коэффициент по горизонтали. Такие "нарастания" по горизонтали и вертикали в точности равны друг другу по самому построению проекции, что и приводит к тому, что проекция сохраняет величины углов. Схематично это изображено на рисунке ниже.

Этот эффект можно представить и немного по-другому: любой участок, в том числе и любой заданный четырехугольник между заданными границами широт и долгот проекция Меркатора растягивает в прямоугольник не равномерно, а тем сильнее, чем ближе к полюсам находятся точки участка.
А вот для проекции Мюфлинга это не так. В цитированной в предыдущей статье брошюре1 рассчитаны локальные изменения масштабов (горизонтального и вертикального) для листов карты масштаба в 1 см 2 км. Подробнее математический аппарат статьи мы рассмотрим немного ниже, здесь лишь отметим, что масштабный коэффициент на всех четырех сторонах трапеции в точности равен единице, а ближе к центру трапеции немного уменьшается2.
Из приведенных выше рассуждений сразу же следует, что говоря в общем, трапецию Мюфлинга невозможно растянуть в прямоугольник Меркатора так, чтобы изменения локальных масштабов совпадали по всей площади карты (если мы растягиваем трапецию равномерно). Иными словами, при таком растяжении мы должны каким-то образом добиться "меркаторской" неравномерности (то есть, растягивать трапецию тем сильнее, чем ближе к полюсу находится растягиваемая часть), а этого невозможно добиться, используя всего лишь четыре точки (по углам трапеции).
Можно посмотреть на проблему и с другой стороны: если бы наша карта изначально была бы изображена в проекции Меркатора, то при равномерном сжатии в трапецию у нас не исчезла бы неравномерность, как минимум, по вертикали (нарастающая с юга на север для Северного полушария). Собственно, именно это и предполагает алгоритм растяжения по четырем точкам: считаем, что карта составлена уже в меркаторской проекции и лишь "подправляем" ее, убирая некоторую "общую деформацию" (здесь и далее, говоря о равномерном растяжении, мы и подразумеваем, что используем лишь 4 точки, то есть тянем трапецию "за углы". В самом конце мы коснемся вопроса использования большего количества точек). А это, как мы видим, не так. Алгоритм заранее не знает, как именно у нас устроены точки растра внутри области привязки и лишь предполагает, что они устроены в точном ожидании с внутренним устройством проекции.
Однако, как же тогда у нас получилось так, что линии сетки меркаторской проекции почти идеально совпали с широтными и долготными метками на минутной рамке карты, изображенной первоначально в проекции Мюфлинга?
Давайте попробуем разобраться.
В упомянутой не раз статье1 приведен подробный математический расчет основных параметров трапеций Мюфлинга для карт масштаба 1:200000 и покрытием 1 градус по долготе и 40 минут по широте, поэтому здесь я подробно цитировать его не буду; заинтересованный читатель найдет исходный текст работы прямо по ссылке. Остановлюсь лишь на ключевых моментах расчета, а также на некоторых особенностях и закономерностях, которые не нашли отражения в статье, но будут полезны для дальнейшего рассмотрения. С этой целью был создан простой калькулятор в Excel, который в целом повторяет рассуждения и вычисления автора3.
Рассмотрим вначале карту двухкилометрового масштаба, расчеты по которой приведены в брошюре. Она ограничена значениями в 40°00'' - 40°40'' по широте и 35°00'' - 36°00'' по долготе. В дополнение к величинам, которые приведены в статье и обозначения которых в калькуляторе в целом совпадают с оригинальными, были добавлены значения промежуточных широт (Ф(1/4) и Ф(3/4)) по высоте листа и промежуточных долгот (L(1/4) и L(3/4)) по его ширине (например, Ф(1/4) = Ф(1) + 1/4*(Ф(2)-Ф(1)) и т.д.). Здесь сразу же отметим тот факт, что доля от общей высоты трапеции Мюфлинга на широте, равной доле от общей разницы широт равна этой второй доле. То есть, при Ф = Ф(1/2) точка на трапеции лежит на высоте равной h/2, при Ф = Ф(1/4) на высоте равной h/4 и т.д. Это прямо следует из вывода формулы (3) статьи1 и пригодится нам в дальнейшем4. А из этого следует, что размер, скажем, минутного деления по вертикальной границе карты строго постоянен.
В дополнение к длинам нижней и верхней сторон трапеции (a(1) и a(2) соответственно), была введена еще величина абсолютного "схождения" s, равная разности этих длин. Сразу же обращает на себя внимание, что величина этой разности для данного конкретного примера получилась равной 837 м на местности (при общей ширине трапеции в 84-85 км). Приводя эту величину к масштабу самой карты, получаем величину около 4 мм, что отлично согласуется с данными, полученными ранее непосредственными измерениями растра на карте примерно вдвое более крупного масштаба.
Стоит также отметить крайне незначительную разницу в длинах боковой (наклонной) стороны трапеции и ее высоты (c и h). Она составляет всего лишь около 1 метра на местности для карты-двухкилометровки, и такая малость является прямым следствием малости угла наклона5 стороны.
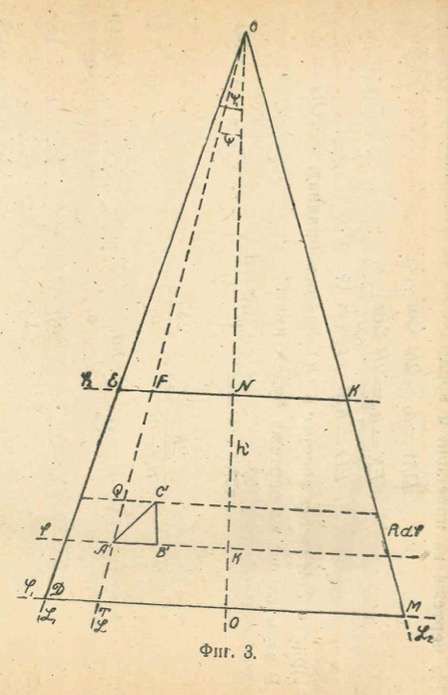
Что же касается самого "угла наклона" Ψ(1) (см. Фиг.3 упомянутой статьи), то велик соблазн приравнять его половине разницы долгот боковых сторон трапеции. Однако это не так: это видно при непосредственных вычислениях в калькуляторе. Этот угол наклона возникает только в промежуточных геометрических построениях (и упрощениях) проекции. Тем не менее, сама малость этого угла и "почти равенство" его сторон c и h позволяет считать половину этого угла представляющей "четверти" L(1/4) и L(3/4) от разности между крайними долготами трапеции (L(2) - L(1)). Это, практически никак не сказываясь на точности вычислений, сильно их упрощает, что и использовано для вычисления масштабных коэффициентов в калькуляторе.
Наконец укажу, что расчетные масштабные коэффициенты, сведенные в единую таблицу, аналогичную приведенной в статье (раздельно для m - масштаба по меридиану и n - масштаба по параллели), показывают, что наименьшего своего значения они достигают ровно в середине трапеции (а это значит, что именно в середине наблюдаются наибольшие искажения реального масштаба на местности в сторону уменьшения; в дальнейшем нам этот факт тоже пригодится).
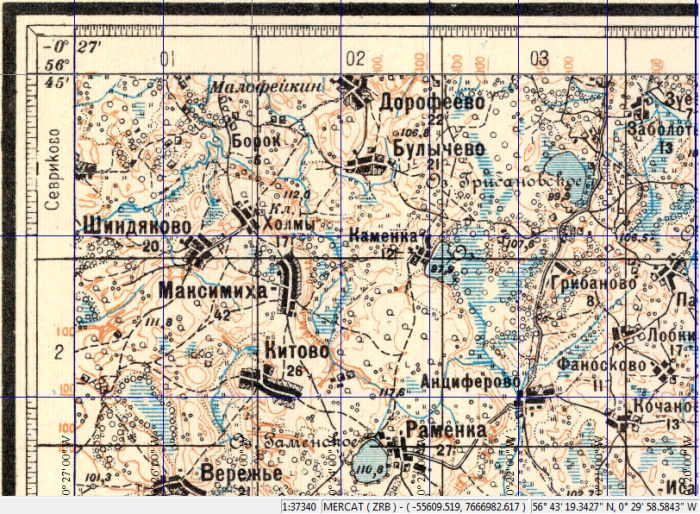
Разобравшись с внутренним устройством проекции Мюфлинга и связанными с ней искажениями обратимся теперь к интересующим нас реальным картам - коллекции одноверстных карт Западного пограничного пространства конца 1920-х - начала 1930-х годов. Поскольку размеры трапеций и искажения внутри их абсолютно одинаковы для заданных границ по широте (для всего заданного горизонтального ряда покрытия), достаточно ограничиться любым вертикальным рядом (колонной). Тогда разумнее всего взять колонну, в которой покрытие, по возможности, максимально при движении с севера на юг. Такие данные можно подобрать; для примера рассмотрим вертикальный ряд с индексом 27. При этом вполне достаточно ограничиться расчетами для самой южной и самой северной границ, а также рассмотреть лист где-нибудь в середине ряда. Поэтому выберем для дальнейших расчетов листы XIc-27 (Копорье), XX-27 (Паричи) и XLIX-27 (Еникиой)6.
Подставим значения крайних значений широт и долгот в калькулятор и выпишем некоторые важные данные. Они сведены в следующую таблицу:

Первое, на что нам следует обратить внимание - это уменьшение величины "схождения" s, как абсолютного, так и относительного (от общей ширины трапеции) по сравнению с трапецией карты-двухкилометровки. При этом также уменьшается "угол наклона" боковых сторон трапеции (она становится более близкой к прямоугольнику). Видно также, что такое схождение уменьшается при переходе от трапеции к трапеции с севера на юг. Что же касается абсолютных значений схождений, то они находятся в диапазоне 155-188 м на местности, или в пересчете на масштаб карты 1:84000 - в диапазоне 1,8-2,2 мм, что отлично согласуется с величиной 2,5 мм, измеренной ранее непосредственно по растру карты.
Далее. Видно, что длины боковых сторон всех трех рассмотренных трапеций c в точности равны друг другу, что следует как из расчетных формул, так и из простых геометрических соображений: для любой трапеции эта сторона является хордой, стягивающей дугу крайнего меридиана трапеции. А эта дуга определена разностью крайних широт трапеции. Равны эти разности - равны длины дуг - равны хорды (для сферы, конечно)7.
Теперь посмотрим на высоты h трапеций. Первое, что бросается в глаза - это то, что они уже почти равны сторонам боковых трапеций (в отличие от карты-двухкилометровки) - но в то же время, немного не равны между собой! Почему так получается? Ведь, казалось бы, эти высоты "представляют собой" центральный меридиан трапеции, а из рассуждений предыдущего абзаца вроде бы должно следовать, что отрезки и на центральном меридиане для равных разностей широт должны быть строго равны между собой? Все дело в том, что высоты наших трапеций не является хордами, стягивающими равные дуги (как в случае боковых сторон), а являются проекциями этих хорд на плоскость трапеции. А поскольку это проекции, то тут-то и заявляют о себе те самые масштабные коэффициенты, к рассмотрению которых мы сейчас и приступим. А здесь сразу отметим, что вся разница в высотах трапеций - на всем диапазоне широт с севера на юг - равна лишь примерно 5 см реального масштаба на местности! В масштабе карты-двухверстки это 0,6 мкм, при предельной точности в 0,1 мм это исчезающе малая величина.
Хорошо, высоты трапеций у нас одинаковы для всех листов, но что происходит внутри карты? Может быть, там есть искажения, которые мы пока не обнаружили, замерив и рассчитав лишь общие размеры трапеций? Однако прежде обратим свое внимание на еще один факт: при переходе от двухкилометровки к карте масштаба 1:84000 все масштабные коэффициенты становятся заметно ближе к единице (с увеличением масштаба уменьшаются искажения).
Рассмотрим наглядный пример. Нарисуем "на местности" довольно большой объект: окружность диаметром 840 м, поместив его в центр самого северного листа (из таблицы выше видно, что масштабные коэффициенты там минимальные, а значит и искажения - самые большие). В масштабе 1:84000 это как раз ровно 1 см. Теперь спроектируем эти точные 840 м на трапецию (пока умозрительно - на местности). С учетом ранее вычисленных масштабных коэффициентов получим для размера по горизонтали (с запада на восток) 840*n(0) или 839,998 м, а по вертикали (с севера на юг) 840*m(0) или 839,995 м. Разница в 2-5 мм для окружности в восемьсот с лишним метров в диаметре! Понятно, что в масштабе карты речь уже идет о сотых долях микрометра, и это для самого искаженного участка.
А теперь важное следствие из вычислений и замечательное свойство проекции Мюфлинга для крупномасштабных карт: если нарисовать на любой карте покрытия в любом месте окружности равного диаметра в метрах, то они и будут выглядеть как идеальные окружности равного диаметра, где бы они не находились - от экватора до полюса. Сравните с окружностями, изображенными на самом первом рисунке для проекции Меркатора8. Таким образом, проекция Мюфлинга на крупных масштабах не только сохраняет форму объектов, но и их размеры - где бы на карте они не находились. Если бы не эти разрывы между листами...
И вот теперь пришло время заняться и проекцией Меркатора и изучить ее поведение внутри границ каждого листа и сравнить с проекцией Мюфлинга.
Составим вначале для выбранных нами листов карт таблицу пересчета угловых координат в прямоугольные - так нам будет проще рассчитывать линейные размеры листов. Такой пересчет легко делается по известным формулам проекции9. В этой таблице для каждого значения широты и долготы, введенных в самую первую таблицу, рассчитываются две координаты в метрах - x (значения по горизонтали) и y (значения по вертикали). Счет начинается, соответственно, от центрального меридиана (Пулковского в нашем случае) и от экватора. Таким образом, рассчитанный прямоугольник соответствует "трапеции Мюфлинга"; в нем также рассчитаны координаты "четвертей" (промежуточных широт и долгот), аналогичные рассчитанным выше. Вынесем также основные параметры получающегося прямоугольника в отдельную таблицу, сходную с той, которую мы создали для проекции Мюфлинга.
Из этих таблиц видно, что для любого листа равные интервалы долгот отсекают равные доли в метрах по ширине прямоугольника, что является прямым следствием "по построению" проекции (можно сравнить с рассуждением выше для проекции Мюфлинга, где это лишь приближенно так, но для крупномасштабных карт выполняется с высокой точностью). А вот для равных интервалов широт все не так: во-первых, в полном согласии с тем, что было сказано в самом начале статьи и со свойствами проекции, при движении с юга на север высоты прямоугольников в метрах возрастают, а во-вторых, все больше начинают различаться их доли: верхняя "половина по широте" всегда больше в метрах нижней "половины", разница между верхней "четвертью по широте" и нижней - еще больше и т.д. И такие различия для самых северных листов достигают уже многих десятков метров на местности!
Казалось бы, уже из этого можно было бы сделать вывод о том, что подозрения об ошибке в предыдущей статье оправдываются полностью: ведь трапецию Мюфлинга с равными интервалами в метрах между равными интервалами широт невозможно растянуть равномерно так, чтобы получились неравные интервалы. Однако, здесь есть одна неучтенная деталь: если посмотреть на размеры получившегося меркаторского прямоугольника, то мы увидим, что его размеры почти вдвое превышают размеры трапеции Мюфлинга "на местности". Это произошло потому, что в отличие от трапеции, которая "висит" в непосредственной близости к земной поверхности, прямоугольник Меркатора спроецирован из центра Земли на поверхность цилиндра, опоясывающего земной шар по экватору, и для средних широт находится где-то в "ближнем космосе" по отношению к земной поверхности.
Очевидно, что трапецию и (или) прямоугольник необходимо каким-то образом вначале смасштабировать, чтобы привести их размеры к "общему знаменателю": ведь в конечном итоге речь идет о представлении одной и той же карты. Может быть, при такой операции (а также при дальнейшей деформации-подправке) нам удастся если не избавиться, то свести к минимуму это досадное различие в свойствах проекций?
Давайте для понимания схематично изобразим, что мы хотим сделать. На рисунке ниже одинаковая длина стрелок символизирует одинаковые "растяжения" для каждой из операций, а разная длина - разные.
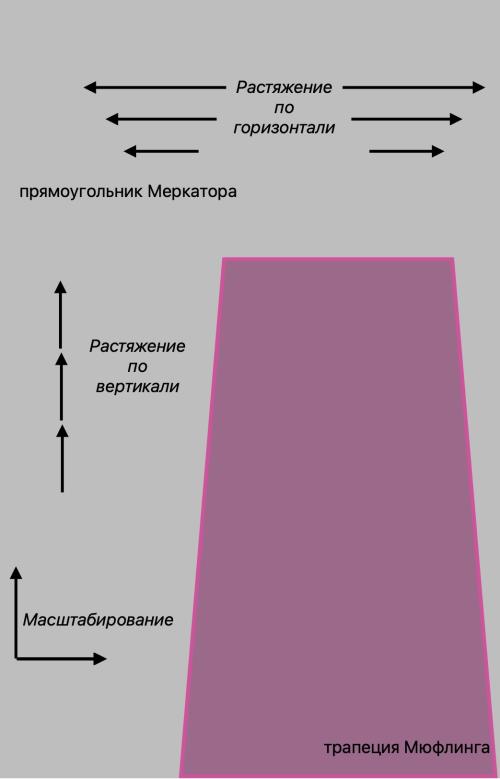
Правда, тут возникает вопрос: каким образом "масштабировать" объекты, имеющие не только разные размеры, но и (возможно) пропорции и (вообще) форму? Можно, например, совместить размеры одной из сторон объектов, а можно - их высоты. Интуитивно кажется правильным совместить основания трапеции и прямоугольника, а затем уже - деформировать (растягивать или наоборот, сжимать) трапецию по высоте, а потом - "доворачивать" ее стороны. Это действительно логично, ведь есть один участок, где основания трапеции и прямоугольника в точности равны - экватор. Нужно только помнить, что такое масштабирование справедливо лишь в пределах одного горизонтального ряда трапеций, а при переходе от одного ряда к другому масштабный коэффициент будет меняться (чтобы отличать его от масштабных коэффициентов, связанных с искажениями той или другой проекции, в дальнейшем будем называть его "коэффициентом перемасштабирования")10.
Составим для каждого листа карты две таблицы: в одну включим масштабные коэффициенты меркаторской проекции (они вычисляются совсем просто, поскольку обратно пропорциональны косинусу широты), а вторая будет содержать итоговые пересчитанные масштабные коэффициенты из таблицы для трапеции Мюфлинга, полученные путем умножения на коэффициент перемасштабирования, а затем исправленные на величину коэффициентов "растяжения по вертикали" и "растяжения по горизонтали". Первый коэффициент (перемасштабирования), в свою очередь можно определить двумя способами: как отношение рассчитанных длин нижних сторон прямоугольника Меркатора (из полученной выше таблицы прямоугольных координат) и трапеции Мюфлинга или прямой формулой - делением длины нижней стороны трапеции на косинус ее широты. Доказательство идентичности результатов же предоставлю вдумчивому читателю.
Для того, чтобы получить значения коэффициентов растяжения, нужно провести некоторые дополнительные вычисления. Они довольно просты. В самом деле, равномерное "растяжение по вертикали" предполагает лишь умножение любого вертикального отрезка на постоянную величину, которой является отношение "желаемой" высоты (то есть, высоты меркаторского прямоугольника) к имеющейся (высоты трапеции Мюфлинга, поправленной на коэффициент перемасштабирования). В следующих двух вспомогательных таблицах и вычислены размеры получающихся трапеций: "смаштабированной на Меркатор" и окончательно "подогнанной по вертикали". А чтобы были понятны величины последовательных изменений, добавлены еще величины абсолютных отклонений получившейся фигуры от "прямоугольника Меркатора".
Стоит обратить внимание, что из данных первой таблицы, а также из расчета коэффициента растяжения по вертикали следует, что до точных размеров "меркаторского прямоугольника" трапецию следует "дотянуть" совсем лишь немного: всего лишь на 2-4% от ее общей высоты. Но самое главное следует из расчетов во второй таблице. Если добавить в нее величины h(0), h(1/4) и h(3/4) (высоты "середины по широте", а также верхней и нижней "четвертей по широте", взятые в метрах), которые были рассчитаны немного раньше для проекции Меркатора и учесть, что при линейном растяжении трапеции эти величины не меняют своих отношений (остаются строго пропорциональными взятой доле от разницы широт верхней и нижней границы трапеции), то мы сразу получим ответы на оба вопроса, поставленных в самом начале статьи.
В самом деле, становится хорошо видно различие между непропорциональным растяжением "по Меркатору" и пропорциональным линейным. Приведу для примера эти различия для самого северного листа нашей подборки. В таблице они выделены цветом.
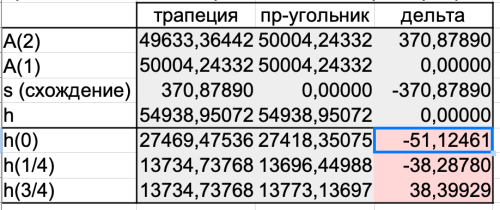
Дальнейшие вычисления можно было бы и не делать: очевидным образом никакое "растяжение по горизонтали" не уберет смещения по вертикали нашего растянутого растра относительно того, что предписано проекцией Меркатора. А такое смещение достигает максимума в середине листов и для самого северного листа имеет величину свыше 50 метров (напомню, что предельная точность масштаба карты-двухверстки составляет 8-16 метров в пересчете "на местность"). В то же время, в масштабе карты такое смещение составляет примерно полмиллиметра, да еще и уменьшается при переходе от северных к южным листам. Именно поэтому его так трудно обнаружить, что называется, "невооруженным глазом", а даже и заметив - списать на дефекты самого растра.
Однако давайте теперь все же закончим с вычислениями и посмотрим на то, какими в результате получились коэффициенты масштабирования по параллелям и меридианам для нашей карты, деформированной указанным выше образом. Они считаются очень просто: перемножаем масштабные коэффициенты на промежуточные величины: коэффициентов "перемасштабирования", растяжения по вертикали и растяжения по горизонтали12. Результаты сведены в последнюю таблицу калькулятора. Из нее видно, что масштабные коэффициенты по параллели в точности равны масштабным коэффициентам проекции Меркатора. А вот для масштабных коэффициентов по меридиану это не так, что является прямым следствием "равномерного" растяжения трапеции по вертикали.
Впрочем, можно оценить и величину такого расхождения. Максимальным оно будет (в отличие от исходной трапеции) на верхней и нижней сторонах. Если же воспользоваться примером выше и построить окружности диаметром в 840 метров "на местности", то после нашего преобразования размеры получившихся фигур будут иметь разницу в размерах по ширине и высоте не превышающую 6 метров, что меньше предельной точности масштаба. Это говорит о том, что наше преобразование очень неплохо сохраняет форму для сравнительно небольших объектов карты. Это дополнительно затрудняет визуальное определение ошибок. Однако для достаточно протяженных объектов (каковым, например, можно считать отрезок от горизонтального края до середины карты) такая накопленная погрешность, как мы увидели выше, становится весьма заметной и сказывается на точности привязки.
* * *
Так можно или нет привязывать крупномасштабные карты, снятые в проекции Мюфлинга в меркаторской проекции, или нет? Ответ прост: it depends. Все зависит от того, что вы хотите получить и чем можете и готовы для этого пожертвовать.
- Если вы готовы добавить ко всем погрешностям привязки и самой карты неустранимую погрешность по вертикали до 50 метров (например, вы делаете обзорное покрытие, где точность не сильно важна), то вполне допустимо использовать исходный вариант способа: привязку по 4 угловым точкам сразу в проекции Меркатора.
- Точность привязки можно увеличить, используя дополнительные точки привязки с промежуточными значениями широт, взятыми с минутной рамки карты. Это позволит добавить в алгоритм растяжения, которым пользуется ваша ГИС недостающую неравномерность растяжения (алгоритм будет видеть, что отдельные участки стоит "тянуть" чуть сильнее или слабее). Недостаток тут очевиден: большая трудоемкость привязки. Следует учитывать также то, что минутные рамки отделены от собственно рамки карты, как правило, дополнительным полем, поэтому без точных "прицеливаний" или даже вспомогательных построений на растре тут не обойтись.
- Наконец, можно попытаться заменить проекцию Меркатора более подходящей проекцией. Тут важно, чтобы она сохраняла важное свойство "мюфлинговских трапеций": точное или "почти точное в рамках допустимых ошибок" равенство интервалов длин в метрах при равенстве интервалов широт или долгот. Такую проекцию вполне можно использовать и в качестве промежуточной, если в конечном итоге нас интересует проекция Меркатора. Такое преобразование с использованием промежуточной проекции математически будет совершенно корректным, ведь первое преобразование сохранит все отношения интервалов, а дальнейшее преобразование в проекцию Меркатора осуществит алгоритм ГИС, который уже точно знает, по каким законам преобразовать известную ему проекцию в другую известную.
- Исходя из соображений предыдущего пункта в качестве такой "промежуточной" проекции можно было бы предложить один из вариантов равнопромежуточной цилиндрической проекции (Equirectangular projection, Equidistant cylindrical projection13). При должном выборе главной параллели искажения длин следует ожидать гораздо меньше "меркаторских". Правда, скорее всего, такой выбор главной параллели будет хорошо подходить лишь к одному горизонтальному ряду карт, однако если планируется в дальнейшем переводить весь большой набор карт, например, в проекцию Меркатора, такое усложнение не является значительным.
- Если же окончательно поступиться принципом "привязывать все и сразу в одной и той же проекции с одними и теми же параметрами", то можно использовать и конические проекции (точно так же, как и в предыдущем пункте, соотвествующим образом выбирая главную параллель или параллели)! В самом деле, ведь участок между заданными широтами и долготами для конической проекции уже представляет собой криволинейную трапецию и у нас нет необходимости ее дополнительно сжимать или растягивать по горизонтали. И к тому же, легко посчитать, что кривизна параллелей для выбранных масштабов и охватов каждой из карт (прогиб дуги окружности относительно стягивающего ее отрезка) настолько мал, что эта дуга практически неотличима от отрезков верхней и нижней сторон "трапеции Мюфлинга".
Литература и примечания
2. Такое поведение проекции очевидно следует из того, что трапеция Мюфлинга лежит на секущей плоскости к земной поверхности. Поэтому в тех местах, где трапеция лежит ближе всего к поверхности сферы (или эллипсоида), искажения минимальны, а в центральной своей части она находится дальше всего от "горба" земной поверхности над ней, что и приводит к относительному сжатию при проецировании этой части на плоскость.
3. Нужно отметить, что автор для упрощения местами использует приближенные формулы. Так, например, во многих местах он заменяет синус малого угла самим углом (в радианах, конечно). А для сферы принимает радиус R "средним для данной трапеции". Из пробных вычислений с помощью калькулятора легко увидеть, что расхождения, возникающие при таких упрощениях, находятся в пределах 1-2 метров даже для абсолютных величин, например, общих размеров трапеции, что в конечном итоге много меньше предельного масштаба карты. Еще меньше это сказывается на разностях и отношениях абсолютных величин. Впрочем, еще надо иметь в виду тот факт, что многие промежуточные вычисления во время написания статьи проводились с помощью тригонометрических таблиц с ограниченной точностью. Замена же синуса угла самим углом приводит к тому, что вместо длины хорды (например, стороны секущей трапеции) мы имеем длину дуги на самой поверхности. Из-за того, что дуга над хордой очень пологая, а угол мал, и получается "почти равенство".
4. Конечно, абсолютная точность будет при том условии, что мы рассматриваем сферу, а не эллипсоид. Но и в случае эллипсоида изменения в пропорциональности будут лежать далеко за пределами точности измерений, см. также предыдущее замечание.
5. Избегая двусмысленности: "угла отклонения боковой стороны от вертикали". В дальнейшем для краткости будем писать просто "угол наклона", подразумевая именно этот угол.
6. Как уже указывалось ранее, размер каждого листа карты 27 минут по долготе и 15 минут по широте, масштаб 1 верста в 1 дюйме, то есть 1:84000, долготы считаются от Пулковского меридиана, который принимается за 0°. Такой выбор центрального меридиана нам никак не помешает, поскольку везде в расчетах листа используются разницы долгот. Более подробно об этих картах рассказано по цитированной ссылке.
7. В дальнейшем перестану каждый раз напоминать о сфере: все дальнейшие вычисления и рассуждения идут для сферы, а "эллипсоидность", как мы уже убедились, вносит поправки, неощутимые на выбранных масштабах.
8. Кстати, такие "окружности" в картографии называются "эллипсами искажения" или "индикатрисами Тиссо".
9. Map Projections - A Working Manual. U.S. Geological Survey, Washington, 1987, pp. 38, 41.
10. Исследование других способов перемасштабирования точно выходит за рамки статьи, на качественном (и даже количественном) результате это никак не скажется, а количество операций и связанные с этим вычислительные погрешности выбранный способ сократит, поэтому таким рассмотрением и ограничимся. Также нет разницы что на что масштабировать: трапецию на прямоугольник или наоборот. Будем увеличивать трапецию, чтобы ее масштабные коэффициенты увеличивались; это снизит относительные ошибки вычислений.
11. Можно было бы сразу составить финальную таблицу и включить в нее итоговые масштабные коэффициенты, полученные в результате трех последовательных операций: масштабирования, растяжения по вертикали и поворота боковых сторон. Однако для демонстрации абсолютных величин изменений в двух последних операциях рассмотрим и промежуточные таблицы.
12. Коэффициенты растяжения по горизонтали очевидным образом (как и показано на схеме) увеличиваются с увеличением широты и меняются от 1 до a(1)/a(2) для любого листа, а промежуточные - легко вывести из свойств средней линии трапеции.
13. Map Projections - A Working Manual. U.S. Geological Survey, Washington, 1987, p. 90.
Вы можете поблагодарить автора этой статьи, например, здесь.