«Параллель Тучкова». Часть седьмая, новогодняя и очень короткая, в которой новых экспертов проверяет эксперт на пенсии

В предыдущей части мы с вами выяснили, что усложнение модели расчета (замена сферы на сфероид) практически никак не сказывается на конечном результате расчета. Следовательно, нет никакой необходимости усложнять модель и достаточно пользоваться более простой моделью сферы.

Напоследок, прежде чем переходить к оценке точности нашего расчета, стоит посмотреть, не влияет ли на эти результаты сам выбор метода. Напомню, что для минимизации суммы квадратов отклонений экспериментальных значений (измеренных углов) от теоретических (вычисленных по формулам для сферы или сфероида) мы использовали метод дифференциальной эволюции.

В то же время, в самом первом исследовании использовались методы Ньютона и сопряженных градиентов, встроенные в инструмент Поиск решения офисного пакета Excel. Давайте ненадолго вернемся на много лет назад и загрузим данные из наших таблиц прямо в тот древний Excel-2003, который я специально по этому случаю достал на старом, неиспользуемом компьютере:

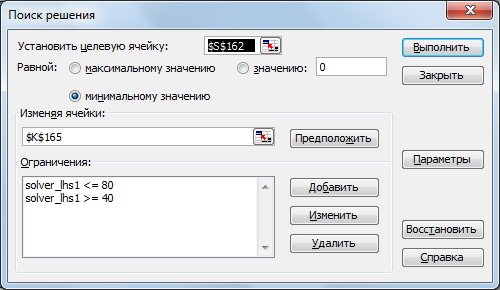
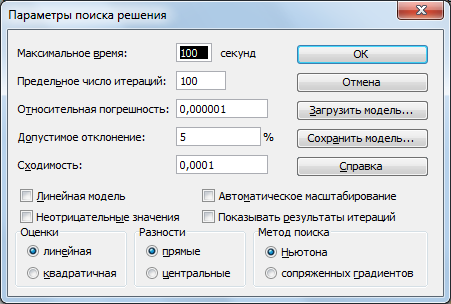
Удивительно, но факт: все настройки (адреса ячеек, ограничения) перенесутся в файле .xlsx в главное окно Поиска Решения, и нам останется только лишь выбрать метод поиска, нажав кнопку «Параметры», оставив все остальные тонкие настройки выставленными по умолчанию.

Сравнение с методом «дифференциальной эволюции» было проведено для обоих методов (Ньютона и «сопряженных градиентов»), а также для обоих вариантов таблиц (для сферы и сфероида). Во всех случаях в качестве стартового приближения использовалось значение широты главной параллели в 65°. Как видно из приведенной ниже сравнительной таблицы, в которой приведены конечные результаты после завершения работы алгоритмов, и которая включена в обновленный файл с расчетами, никакого влияния на результат выбор метода не оказывает.

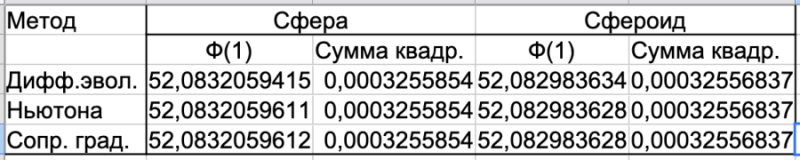
Итак, мы с вами продемонстрировали практическую независимость используемой нами методики от конкретных численных методов расчета (модели и алгоритма минимизации). Это поможет нам (уже в следующем сезоне) в статистической оценке точности и достоверности полученных результатов.