Объединенные электронные атласы из многолистовых крупномасштабных карт XIX-XX веков. Введение.

«... первые догадки о новом устройстве вещей чрезвычайно
ценны, потому что стимулируют следующие версии и часто
определяют, в каких терминах следует думать о задаче».
Алексей Семихатов. «Сто лет недосказанности»

Андрею Мачинскому, из-за которого мне всегда приходилось думать об этих вещах.

Когда я задумал этот цикл статей, я не предполагал никакой сколько-нибудь масштабной работы. Мне хотелось лишь в двух-трех статьях изложить обновленный подход к привязке исторических карт и изготовлению из них объединенных, «склеенных» покрытий, пригодных для размещения, в первую очередь, в Интернете, а также обсудить проблемы точности имеющихся привязок, которые я не раз поднимал.

Однако, чем дальше я погружался в работу над этим простым планом, тем больше я понимал: текущее состояние дел как с привязкой карт вообще (не говоря уже об сложных исторических картах), так и с созданием из них единых покрытий крайне далеко от идеального, и даже — сколько-нибудь логически законченного. Между тем, несмотря на огромную работу, которая была проведена за истекшие примерно два десятка лет, создание такого рода покрытий продолжает оставаться актуальным и сегодня. Ведь такие карты нужны очень многим: краеведам, изучающим родной край, туристам, которые пользуются этой краеведческой деятельностью, историкам, которые при работе в архивах постоянно сталкиваются с той сложностью поиска документов, когда надо знать административное деление местности на определенный период, поисковикам, которые занимаются исследованием мест прошедших боев и находят ранее неизвестные захоронения погибших, всем тем, кто интересуется происхождением своих предков, а также многим и многим другим.

Ниже я коротко изложу то, что представляет собой такое состояние на сегодняшний день, однако сразу же хочу сделать еще одно замечание. Кажется, что до сих пор не существует ни одного сколько-нибудь подробного и цельного учебника по привязке карт. Имеющиеся руководства (разнообразные «мануалы» и «туториалы») как правило ограничиваются лишь самыми простыми случаями, например, для демонстрации возможностей той или иной программы, не давая никакой теоретической основы — почему что-то надо делать именно так, а не иначе. Имеющиеся же теоретические заметки обычно касаются лишь одной, совершенно узкой темы, оставляя за бортом общую картину. Именно поэтому возникла еще одна идея — постараться изложить не только основы метода, но и сделать такое изложение максимально похожим на учебник, с тем, чтобы любой желающий читатель смог повторить результаты, а при желании — применить полученные знания для самостоятельной работы с собственными картами, и даже — не обязательно историческими. Причем, поскольку сама идея цикла предполагает не только привязку индивидуальных карт, но и их объединение в большие покрытия, для «учебника» она также оказалась бы полезной, поскольку именно на процессе объединения проще всего понять, как на практике выглядят те или иные теоретические построения.

В процессе такого способа изложения нам придется много раз сталкиваться с объяснениями терминологии, то есть с определениями. Основной блок с изложением этого планируется в одной из следующих частей [1], здесь же я хочу дать немного пояснений, касающихся самого названия цикла.

На самом деле, придумать заголовок, который бы коротко излагал саму идею цикла и в то же время не упускал из виду каких-то существенных деталей, оказалось совершенно невыполнимой задачей. Поэтому пришлось в нем отразить лишь основное, а вот о некоторых деталях и подробностях я скажу здесь в нескольких словах.

Начну с конца заголовка. Под «крупномасштабными» картами мы будем понимать все карты масштаба 1:100000 (1 километр в 1 сантиметре) и подробнее. Поскольку масштабы карт XIX века отличаются от принятых в веке XX, и как правило, выражаются в верстах в дюйме, здесь я проведу границу немного по-другому (впрочем, вполне в согласии с принятой в то время) и отнесу к крупномасштабным карты масштаба 1:126000 и подробнее. Это позволит нам с вами считать «крупномасштабным» один из основных продуктов российской картографии XIX века — военно-топографическую трехверстную карту.

Но на самом деле, крупномасштабными картами в изложении я не буду ограничиваться. Некоторые базовые концепции и практические примеры намного проще изложить как раз с использованием среднемасштабных карт, которые мы с вами будем считать лежащими в диапазоне выше крупномасштабных и до 10 верст в дюйме (что примерно соответствует четырехкилометровому масштабу в стандартах XX-XXI веков). В виде исключения я буду иногда даже обращаться к картам еще более мелких масштабов, например, к карте-«миллионке» второй половины XX века (масштаб 1:1000000 или 10 км в 1 см), но только эпизодически и для демонстрации некоторых приемов, которые на картах более крупных масштабов гораздо труднее пояснить. Так что будем считать, что заголовок я подсократил лишь для удобства восприятия, а этого пояснения достаточно для представления об общей картине цикла, тем более, что основной упор мы с вами будем делать все же на крупномасштабные карты.

Но нас с вами будут интересовать не все карты, а именно многолистовые. Это значит, что мы оставим вне нашего поля зрения такой огромный массив, как например, планы городов. А самое главное — «многолистовость» подразумевает, что такие карты покрывают обширную территорию. Ими мы с вами и ограничимся, причем сразу же еще больше ужесточим и формализуем отбор: нас будут интересовать карты, покрывающие территории от губернии (области) и выше. На самом деле таких карт известно сравнительно немного, но зато мы сможем изучить их более подробно.

Покончив на время с масштабами и покрытиями, обратимся теперь к первой части заголовка. Что я подразумеваю под «объединенными электронными атласами»?

Понятнее всего здесь выглядит слово «атлас». Как известно, атласом в картографии называют «систематизированное собрание карт, вы­пол­нен­ных по еди­ной про­грам­ме, и из­дан­ное в ви­де кни­ги, ком­плек­та лис­тов в пап­ке в од­ном или не­сколь­ких то­мах или в элек­трон­ной фор­ме как це­ло­ст­ное про­из­ве­де­ние» [2,3]. А «электронные» эти атласы потому, что нашей с вами целью будет создание из необработанных, сырых сканов бумажных карт конечного произведения, пригодного для отображения в ГИС или даже просто в окне браузера, причем произведения геопривязанного, то есть такого, у которого каждая точка изображения имеет определенную географическую координату. Вполне естественно, что такой продукт должен существовать в электронном виде.

Наконец, про слово «объединенные». Это и будет основной целью нашей с вами работы. Создать отдельный геопривязанный лист карты довольно просто, в самом начале цикла мы с вами это обязательно разберем. Сложности начинаются, когда мы пытаемся объединить (или, как часто говорят, употребляя жаргонизм, «склеить») такие листы в единое покрытие, причем без искажений: перехлестов, разрывов, нелинейных деформаций и т.д. Более того, во многих случаях приходится выполнять и дополнительную работу, например, жертвовать перекрывающимися частями зарамочного оформления карты с тем, чтобы они не мешали отображению основной картографической информации внутри рамки, ведь нас интересует, как мы видели чуть раньше, «целостное произведение».

Итак, давайте теперь коротко рассмотрим, в каком состоянии находится частная задача — привязка (см. примеч. [1]) исторических карт и более общая, построенная на частной — создание объединенных покрытий.

Начнем с наиболее обширной группы работ, в которой сконцентрировались как отдельные успехи, так и многочисленные ошибки и недостатки. Кажется, почти без преувеличения можно сказать, что по такой методологии создавалось не менее 90% широко известных покрытий. Основной отличительной особенностью таких работ является то, что привязка первичного картографического материала (сканов исторических карт) осуществлялась без учета системы координат (СК) исходной карты и ее отличия от современной СК, или без учета проекции, в которой эта карта была составлена, или с использованием контрольных точек привязки, верность которых никак не подтверждалась и даже не оценивалась. Зачастую все эти ошибки присутствуют в таких работах не по отдельности, а «полным списком». Методологически все это выглядит так: берутся сканы листов карты (очень часто — плохого качества), на них находят некоторые объекты, которые, как представляется, можно было бы соотнести с современными (для которых известны современные координаты) и «привязываются» в какой-нибудь современной системе координат (часто берут WGS 84), и проекции попроще (например, меркаторской). Или же осуществляют ту же привязку с использованием координатной сетки, изображенной на карте, полностью отождествляя координаты этой сетки с современными. После чего, полагаясь на возможности современной программы, запускают процесс трансформации, причем в автоматическом режиме, ожидая, что на выходе получится, в целом, тот же растр, но уже имеющий современные координаты.

Удивительным образом эта методика (в целом взятая из опыта привязки небольших фрагментов современных карт, или планов, или фрагментов спутниковых снимков)  иногда работает и иногда (на самом деле, очень редко!) дает вполне приемлемые результаты. Однако, эти результаты, если и оказываются «приемлемыми», то для каждого листа по отдельности. Непреодолимые сложности начинаются как раз на втором этапе: попытке свести отдельно привязанные листы в единое покрытие. Вот тут в полной мере и проявляются все те «перехлесты, разрывы и нелинейные деформации», о которых шла речь выше.

Давайте коротко рассмотрим, почему так происходит, потому что это рассмотрение нам поможет при обсуждении других, более корректных способов. А коротко — потому, что мы с вами еще не добрались до теоретических основ, поэтому неподготовленному читателю тут придется принять эти объяснения на веру, а полное понимание наступит тогда, когда мы с вами освоим основы теории. Поэтому постараюсь объяснить здесь это совсем просто, буквально «на пальцах».

Начнем с влияния выбора системы координат. Хорошо известно то, что использование современных координат, взятых в системе WGS 84, даже для карты, изображенной в довольно близкой по параметрам системе СК-42, может привести к ошибке на местности в многие десятки метров. Для систем координат XIX-го века такие ошибки могут достигать уже сотни и даже многие сотни метров! Это происходит потому, что координатные оси разных систем координат, во-первых, сдвинуты друг относительно друга, а во-вторых, еще к тому же и повернуты в пространстве. Эти сдвиги и повороты учитываются в параметрах преобразования одной системы координат в другую для того, чтобы с некоторой приемлемой точностью совместить эти две разных системы. Мы с вами будем рассматривать это подробнее, когда дело дойдет до создания собственных систем координат. Пока же просто примем следующее: неучет этих параметров, а тем более, отождествление двух принципиально разных систем — самый главный источник ошибок с координатами объектов на привязанной таким способом карте.

Часто бывает, что о таких различиях осведомлены — и тогда используют другой метод: приписывают современные значения координат, объектам на старой карте, которые, как предполагается, можно соотнести с современными, для которых эти значения можно либо измерить непосредственно на местности, либо получить из точных и достоверных источников, например, спутниковых снимков. Однако здесь подстерегает другая неприятность: на самом деле таких объектов очень мало. В качестве их не подходят детали рельефа (за десятки и сотни лет рельеф местности может измениться до неузнаваемости). Разнообразные водные объекты также не годятся (например, русла рек меняют свое положение), тем более не подходит растительный ландшафт. Даже объекты, казалось бы, капитального строительства со временем перемещаются (например, дороги вместе со своими перекрестками, мосты — ведь часто новый мост строят не точно на месте старого, чтобы не прерывать дорожного сообщения, — и т.д.). Для таких объектов подходят лишь отдельно стоящие здания (например, церкви) и как исключения — перекрестки улиц внутри исторической застройки городов. Но и в этом случае для каждого такого объекта необходимо подтверждение в источниках о том, что создан он был раньше, чем была составлена карта, а в результате перестройки не изменил своего отмеченного на карте местоположения. Все вышесказанное учитывают очень редко — и это также приводит к серьезным ошибкам с координатами привязанной карты. В общем, мораль здесь проста: всегда следует помнить о том, что координаты, указанные на исторической карте, были точны для своего времени (для той системы координат, которая использовалась при ее составлении), но могут отличаться, и очень сильно, от современных значений. Для иллюстрации изложенного приведу анимацию, которая была получена совмещением участка карты Тверской губернии из трех различных источников с фиксированной в современных координатах рамкой. На ней видны различия в координатах, достигающие для разных проектов величин в сотни метров.

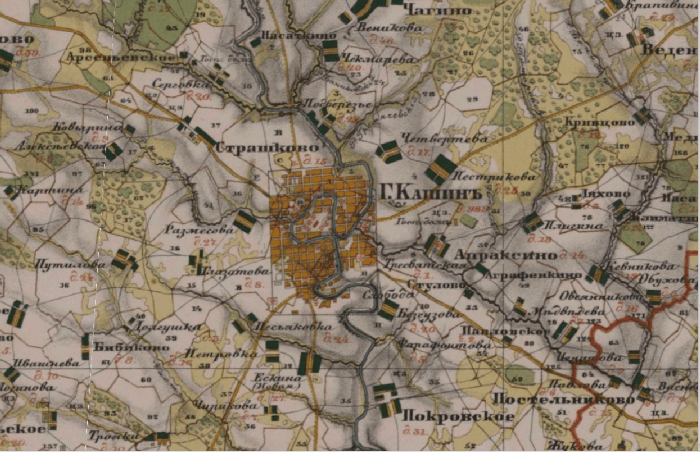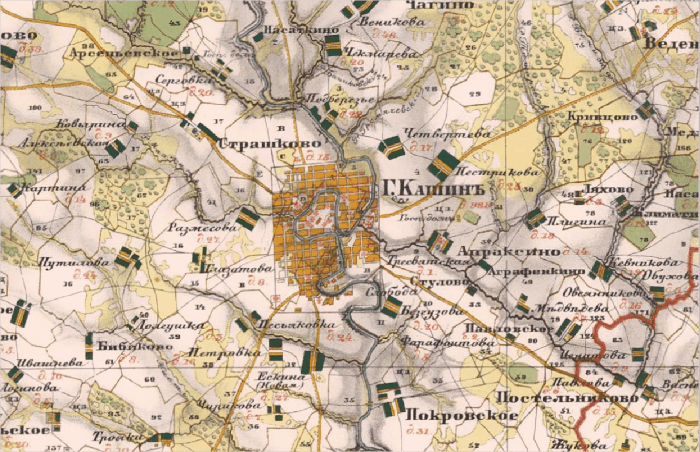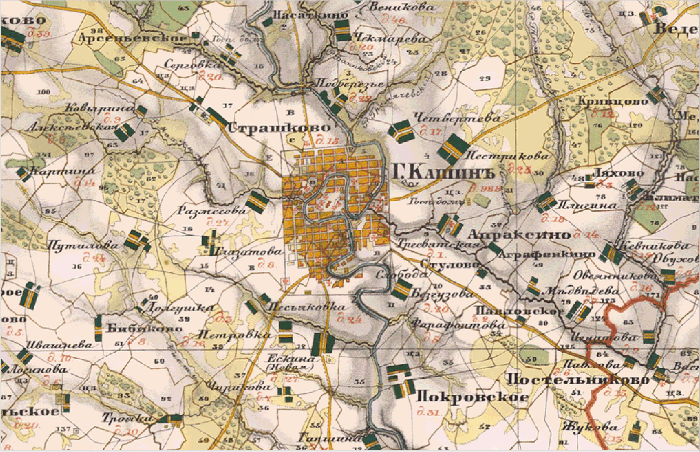
Теперь давайте посмотрим, к чему приводит использование для привязки проекции, не совпадающей с проекцией исходной карты. Логика такого приема понятна: проекция оригинала достоверно известна далеко не всегда, а расчет делается на то, что алгоритм трансформации исходной карты, который будет использован при привязке, сам справится с задачей, деформировав карту в нужных направлениях. Об этих трансформациях мы подробно поговорим в теоретической части, здесь же я лишь обращу внимание на очень простую вещь для понимания: алгоритмы трансформации растра, которые используются при привязке, практически не имеют ничего общего с алгоритмами, используемыми при перепроецировании растра. В процессе привязки используются самые простые преобразования точек растра: чаще всего линейные, реже — простые полиномиальные (со степенью полинома не выше третьей), еще реже — некоторые комбинации полиномиальных преобразований для различных участков карты. Процесс же перепроецирования карты имеет по самой своей сути другую природу: каждая проекция, как правило, выражается набором нелинейных уравнений (включающих в себя, например, сложные тригонометрические функции и переводящих географические координаты в плоские, прямоугольные координаты проекции) и переход между этими функциями требует совсем других, нелинейных расчетов. А самое главное — для того чтобы перепроецирование работало правильно, его алгоритмы должны «знать» не только целевую проекцию карты, но и исходную. Алгоритм же привязки сам по себе ничего не знает о первоначальной проекции карты, и именно поэтому в нем используются совсем простые преобразования. Да, безусловно, как мы увидим в дальнейшем, всегда можно постараться и набрать достаточное количество контрольных точек, с тем чтобы буквально «натянуть» растр на них, при этом используя самые сложные алгоритмы трансформации из доступных. И если этих точек достаточно много, то карта в их окрестностях получается довольно хорошо привязанной. Но только в их окрестностях! Платой за это является то, что все деформации растра уходят в области карты, которые находятся достаточно далеко от контрольных точек. А поскольку количество таких точек всегда ограничено, то при таком подходе всегда будут существовать довольно обширные области, где деформации достигают совершенно неприемлемых значений. Иллюстрацией этого может служить привязанная довольно давно и примерно по таким методикам среднемасштабная Специальная десятиверстная карта Российской империи, где такие искажения видны просто невооруженным глазом и достигают уже даже не сотен метров, а километры.

Совершенно очевидно, что если индивидуальный лист такой карты имеет такие приобретенные в процессе привязки дефекты, как еще на одном рисунке ниже, то ни о какой «склейке» без разрывов, нахлестов и дальнейших деформаций его (и соседних с ним) листов вести речь просто нельзя.

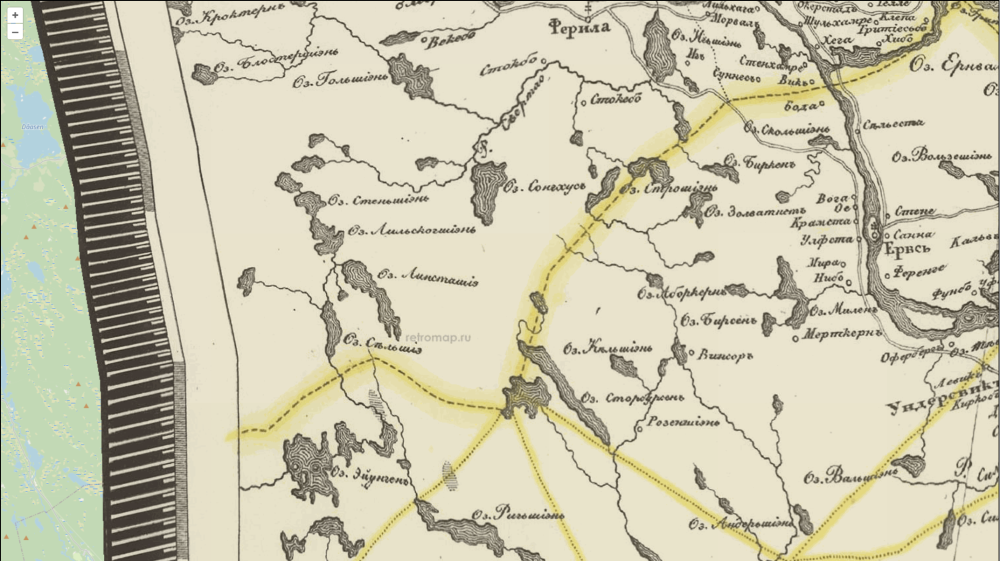
Последнее замечание здесь будет скорее не теоретическим, а техническим. Современные ГИС в процессе привязки позволяют использовать автоматический выбор алгоритма трансформации в зависимости от количества используемых контрольных точек. При этом, чем больше точек используется в таком режиме, тем более «нелинейный» алгоритм «может позволить себе» ГИС, причем вполне самостоятельно. Неучет этого простого фактора или пренебрежение контролем над используемым алгоритмом — еще один источник искажений и ошибок.

Если подвести итог этим рассуждениям, то ошибки в выборе системы координат влекут за собой существенные ошибки в положении привязываемой карты, а ошибки в выборе проекции и алгоритма трансформации отвечают за неконтролируемые деформации итогового результата.

Существенный прорыв в этом направлении произошел примерно в 2007 г., когда начался многолетнетний и обширный цикл работ В.Г. Щекотилова и сотрудников. Важные промежуточные результаты их были обобщены в сборнике [4], а в дальнейшем работа углублялась и расширялась [5]. За более чем десять лет работы авторами были привязаны почти все доступные в то время крупно- и среднемасштабные карты XIX в., а самое главное — была разработана методика, которая получила свое практическое воплощение в тех самых объединенных электронных атласах, о которых шла речь в самом начале этого введения [6].

Пожалуй, наиболее существенное значение в работах В.Г. Щекотилова и сотр. имеют две вещи. Первое — они обратили специальное внимание на то, что практически все многолистовые наборы исторических карт (и «бумажных» атласов) представляют собой так называемую «эквидистантную сетку», то есть практически каждый лист карты конкретного набора (например, карты Менде по Тверской губернии) имеет строго определенные и постоянные в этом наборе размеры (за редкими исключениями, касающимися отворотов, клапанов, неполных листов и т. д.). Эта сетка может быть представлена и в виде такой же равномерной сетки прямоугольных координат на местности. Удивительно, но почему-то авторы не сделали еще полшага вперед и не зафиксировали явно очевидное следствие из этого: такая сетка полностью совпадает с прямоугольной (декартовой) сеткой координат, рассчитанной в системе координат исходной исторической карты с учетом ее проекции и в тех единицах длины, которые были приняты во время ее создания. Возможно это произошло из-за того, что они почему-то старались обходить вопрос системы координат и проекции исходной карты, и я об этом обязательно скажу немного ниже [7].

Второе очень важное замечание было сделано авторами в самом начале работ. Это была фиксация того факта, что для того, чтобы привязанные листы можно было бы объединять в единое покрытие, их исходную, прямоугольную форму нельзя деформировать. То есть при привязке нельзя использовать ни нелинейные (полиномиальные) трансформации, ни даже линейные преобразования, которые образуют скошенные фигуры. Это привело их к естественному выводу: максимальное количество параметров, которое может быть использовано в таких привязках для работы алгоритма трансформации может быть не более 6, то есть это может быть лишь так называемое преобразование подобия [8,9]. К слову, есть один удивительный факт: кажется, что на тот момент в программном обеспечении, которым пользовались авторы, именно этот алгоритм был не реализован, и им пришлось для этого самостоятельно разработать целый расчетный аппарат.

Коротко постараюсь описать методику авторов (конечно, с некоторыми упрощениями). Вначале из всего многолистового покрытия выбираются несколько карт (от нескольких штук до нескольких десятков). Авторы называют их «пробными», на самом деле они — опорные, эталонные. Далее осуществляется привязка (авторы называют этот процесс «регистрацией») эталонных листов в некоторой системе координат и в некоторой проекции [10]. Затем рассчитываются прямоугольные (декартовы) координаты углов каждого эталонного листа в выбранной проекции. После чего решается оптимизационная задача (фактически, методом наименьших квадратов определяется средний размер ячейки «эквидистантной сетки» (а следовательно, и средний размер листа в единицах проекции) и его поворот относительно прямоугольной сетки этой некоторой проекции. Полученный результат можно продемонстрировать рисунком ниже, где изображена такая рассчитанная сетка для эталонных листов карты Ярославской губернии [11].

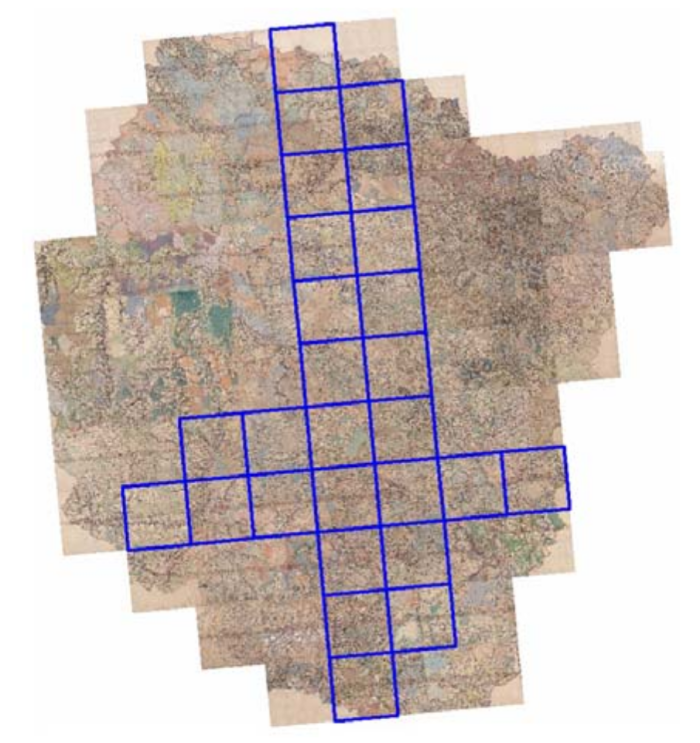
Теперь, когда известен шаг сетки и ее поворот в выбранной системе координат, можно рассчитать прямоугольные координаты узлов сетки и для оставшихся листов. А по полученным координатам уже привязать и оставшиеся листы. Интересно, и очень полезно то, что на оставшиеся места «эквидистантной сетки» можно привязывать неполные листы или даже фрагменты листов [12].

Часть проделанной авторами работы схематично изображена на рисунке ниже, взятом из статьи [5]. На нем приведены сетки всех карт Менде по поволжским губерниям. Не должны удивлять разные размеры для ячеек сетки: для каждой многолистовой карты по определенной губернии они индивидуальны. Кроме того, индивидуален и поворот сетки относительно сетки координат общей проекции, в которой изображена эта сводная карта, поскольку каждая группа оригинальных листов имеет свои, индивидуальные параметры проекции (в частности, центральный меридиан, к которому жестко «прикреплена» сетка листов).

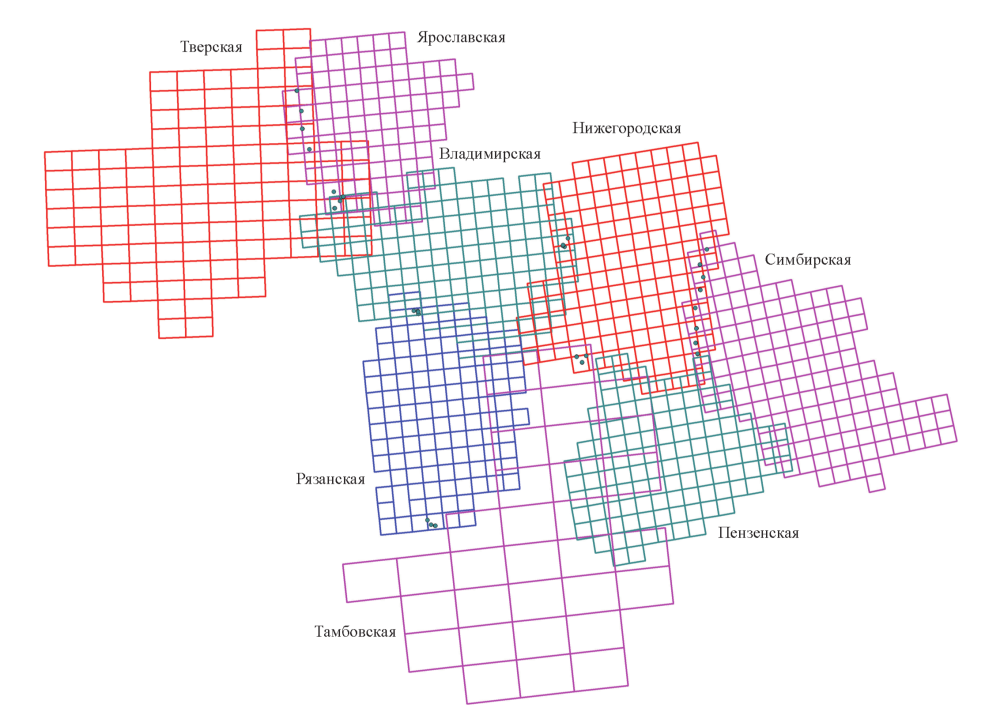
Теперь перейдем к недостаткам и ошибкам описанной методики. Здесь я постараюсь расположить их в порядке убывания значимости: от самых, на мой взгляд, существенных, к менее заметным, но которые, тем не менее, хотелось бы перечислить и иметь в виду при дальнейшем изложении.

Первого, и самого главного я уже коснулся выше, когда употребил слово «некоторой» в применении к системе координат, в которой привязывались карты. Здесь авторы совершили ту же существенную ошибку, о которой шла речь выше, когда мы с вами обсуждали полный набор «неправильных» методов. Дело в том, что всегда и везде на стадии привязки («регистрации») эталонных («пробных») карт авторы используют систему СК-42. Разница же географических координат одной и той же точки, взятой в системе координат карты XIX в. и СК-42, как мы видели раньше, может достигать десятков секунд и даже нескольких минут. В пересчете на линейные меры — это сотни метров. Таким образом, «приписав» точке карты координаты, которые отмечены на самой карте, те же самые значения для системы СК-42, мы на эти сотни метров и ошибаемся. Но авторы именно так и поступают, в большинстве случаев используя градусную сетку самой карты [13]. Правда, иногда они упоминают и возможность и привязки карты «по координатам объектов» [14], но нигде не говорят о том, что они реально это делали и тем более, не оценивают достоверность такой привязки (об этом тоже речь шла выше) и не приводят список таких объектов.

Хорошим примером такой ошибки может послужить снимок экрана, приведенный ниже, который взят непосредственно с сайта одного из проектов авторов. В правой его части на современной карте отмечена перекрестием примерная середина железнодорожного моста через Волгу в г. Тверь. Здесь есть исключение из того, что я говорил выше: достоверность того, что этот же мост изображен на карте Менде не вызывает сомнений, мост построен в 1849 г., а история его реконструкций также хорошо известна. Не вызывает сомнений и положение русла реки внутри или рядом с исторической застройкой. Однако, если мы с вами посмотрим на то же перекрестие в левой части изображения (с исторической картой), то увидим, что все изображение смещено с севера на юг почти на 400 метров.

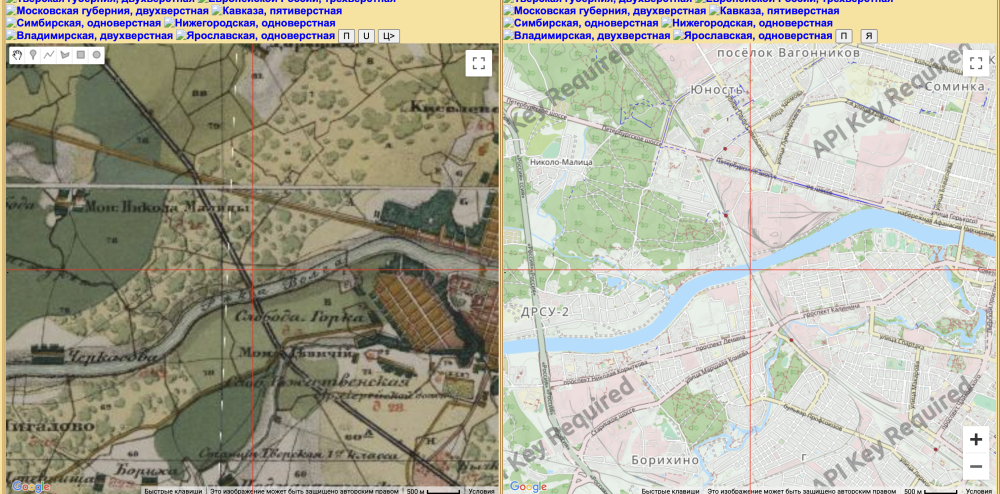
Справедливости ради здесь следует обязательно сказать, что авторы осведомлены о таких погрешностях, более того, во многих статьях они их приводят. Так например, для военно-топографической трехверстной карты ошибки оцениваются в диапазоне 100-650 м [15]. Для одноверстной карты Нижегородской губернии максимальная ошибка составляет (в пересчете из угловых на линейные единицы) около 450 м, а для одноверстной карты Ярославской губернии — свыше 700 м [13]. Это довольно большое расхождение. Стоит сказать, что причины его авторы видят в «охватываемой картой площади, деформациях листов, различия данных на архивных и современных картах, низкого разрешения сканирования» [15], однако, на мой взгляд, главный вклад в такое расхождение вносит использование «чужой» для карты системы координат.

Вторым, не совсем очевидным, но как мне представляется, также значительным по величине источником погрешностей в положении привязанной карты, является сама методика расчета «эквидистантной сетки». Как мы с вами видели немного раньше, размеры такой сетки вычисляются в ходе решения оптимизационной задачи. А это значит, что такие размеры всегда будут содержать некоторую случайную ошибку (погрешность). Причем эта ошибка будет сохраняться вне зависимости от представления эквидистантной сетки: считаем ли мы ее размеры «на местности» или пересчитываем с учетом масштаба карты в исходный размер листа, соответствующего этой сетке. Так, для листов военно-топографической трехверстной карты (возьмем ее для примера, хотя все последующие рассуждения качественно справедливы и для всех других многолистовых карт) авторами были получены значения ширины и высоты ячейки такой сетки 73827.73 м и 52890.45 м соответственно, что в пересчете в масштаб исходной карты даст величины 23.07 на 16.53 дюйма [16]. В то же время известно, что листы карты должны иметь строго определенный физический размер в 23 на 16.5 дюйма ровно [17]. К сожалению, авторы никогда и нигде не учитывают сам факт существования такого рода «теоретических» размеров эквидистантной сетки и не делают на это никаких поправок, а всегда используют для дальнейшего построения данные, вычисленные в результате решения оптимизационной задачи. Хотя казалось бы, совпадение теоретических значений с расчетными получается довольно хорошим, однако давайте внимательнее посмотрим на то, что происходит в действительности.

Возьмем для примера получившуюся ширину листа. Она получилась больше «теоретической» всего лишь на 0.07 дюйма (примерно на 1.7 мм). Если мы с вами мысленно зафиксируем один из углов карты в точно определенной нами точке местности (предположим, что мы абсолютно безошибочно можем определить ее реальное положение), то противоположный по ширине край карты даст нам ошибку с учетом масштаба карты примерно в 217 м. Величина немаленькая, но все еще терпимая и ее можно списать на обозначенные авторами причины расхождений (см. цитату выше). Но это касается размеров одного листа, а мы же с вами помним, что из таких ячеек построена вся «эквидистантная сетка»! И вот тут происходит очень серьезная методологическая ошибка: случайную погрешность измерений авторы превращают в систематическую. «Пристыковав» к первому листу по ширине еще один лист, мы с вами получим суммарное отклонение для дальнего от нашей «безошибочной» точки края уже в 434 м. Для третьего — 651 м и так далее, а учитывая то, что многолистовые покрытия могут содержать до нескольких десятков листов как в ширину, так и в высоту, у нас с вами может накопиться погрешность в километры. Иными словами, произвольная случайная ошибка в определении размеров сетки становится постоянной и суммируется столько раз, сколько листов мы достраиваем к эталонным листам. Это и есть систематическая ошибка.

Наконец, третий источник погрешностей (правда, он представляется мне гораздо меньшим по влиянию на точность положения карты) — это использование той самой некоторой проекции вместо точно определенной оригинальной проекции карты (конической или псевдоконической). В качестве таковой авторы всегда используют проекцию Гаусса-Крюгера. В определенном смысле эта проекция является «хорошей», то есть дает гораздо меньшие искажения форм, чем, например, проекция Меркатора. Однако если мы с вами вспомним то, что говорили раньше про перепроецирование, станет понятно, что преобразование исходной проекции в проекцию конечную по своей сути нелинейно. А это, в частности значит, что любой прямоугольник (каковым является исходный лист карты) не может быть изображен в проекции Гаусса-Крюгера в виде прямоугольника. И наоборот, в сетку, рассчитанную в проекции Гаусса-Крюгера в виде строгих прямоугольников нельзя поместить прямоугольный лист карты без его нелинейной деформации. Тем более, что авторы, как мы помним, запретили такие нелинейные деформации (чтобы избежать искажений) использованием преобразования подобия. Можно сказать и так: прямоугольник в исходной проекции карты и прямоугольник в проекции Гаусса-Крюгера — две совершенно разные сущности с отличающимся содержимым внутри себя, даже если имеют полностью одинаковые размеры,  и не могут быть совмещены «точка в точку» никаким линейным преобразованием. Впрочем возможно, что такие нелинейные нестыковки могут оказаться пренебрежимо малыми (как я уже сказал выше, проекция Гаусса-Крюгера в этом смысле является «хорошей» проекцией). Однако же авторы нигде и никак явно это не обсуждают и тем более не оценивают количественно. Более того, мне представляется, что именно это является первопричиной возникающих при «склеивании» листов отдельных разрывов и нахлестов, которые порой можно видеть достаточно явно и пример которых приведен на рисунке ниже.

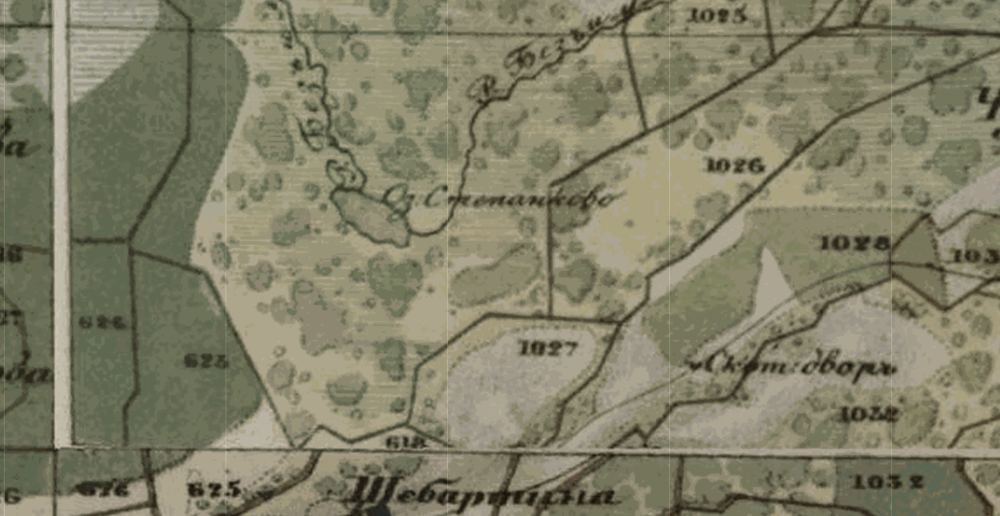
Таким образом, к достоинствам методики, разработанной группой, можно отнести, в первую очередь, системный подход к проблеме, что позволило им первыми осуществить относительно точную привязку обширных цельных покрытий (электронных атласов) без заметных искажений исходных карт. В то же время, ошибки или сознательные допущения, касающиеся систем координат и проекций, позволяют говорить о том, что методика поддается дальнейшему, достаточно значительному улучшению.

Без малого 13 лет назад на основе известной, достаточно разрозненной, но обширной информации мной был обобщен и изложен в виде методики и еще один, альтернативный способ привязки исторических карт [18]. Его можно разложить на стадии, которые я коротко перечислю ниже. 

Подготовительная часть начинается с выявления информации о проекции исходной карты, ее системе координат, а также об исходном, «теоретическом» размере ее листов. При необходимости в используемом программном обеспечении создается система координат, свойственная исторической карте. Затем осуществляется предварительная коррекция исходных растровых файлов (сторонним программным обеспечением) с тем, чтобы как можно лучше убрать искажения геометрических размеров и «подогнать» их под желаемый, «теоретический» размер. Далее проводится оценка точности, которой следует придерживаться при дальнейшей работе. В первую очередь она зависит от масштаба исходной карты и разрешений доступных ее сканов.

Следующий «блок» описывает собственно привязку. Она начинается с выявления контрольных точек для привязки, которыми могут служить как традиционные пересечения линий параллелей и меридианов, изображенные на карте, так и углы рамки листа карты, а также точки пересечения параллелей и меридианов с рамкой. С этой целью был разработан специальный калькулятор [19], который (на примере проекции Бонна для военно-топографической трехверстной карты) позволяет осуществить такие расчеты. Затем осуществляется собственно привязка — в той системе координат, которая была определена (и при необходимости, создана) на начальном этапе. Также используются «родные» для карты параметры проекции.

На заключительном этапе карту, привязанную в «исторической» системе координат следует скорректировать путем подбора пересчетных параметров (трех или семи) в современную систему координат. Для этого вначале определяется отдельный набор точек, которые будут участвовать в таком пересчете. Важно, чтобы эти точки могли быть определены как на исторической карте, так и на современной местности. Для этого было предложено использовать координаты церквей, построенных до времени создания карты и сохранившихся до настоящего времени. Такие координаты определяются на привязанной исторической карте (в «исторической» системе координат) и затем находятся в современной системе — или с использованием доступных источников, например, на привязанной современной карте, или непосредственно на местности. После чего специализированными программами осуществляется поиск параметров пересчета из исторической СК в современную. Полученные параметры позволяют создать еще одну систему координат, но уже связывающую через них историческую и современную, которой и заменяется промежуточная историческая система.

Описанная методика давала очень хорошие результаты при привязке индивидуальных карт, гораздо лучшие, чем имеющиеся в то время. Однако и она не была лишена многих недостатков.

Первое: она была достаточно трудоемкой. Работая в русле тогдашних представлений о том, что «чем больше контрольных точек взять, тем точнее получится привязка» всегда хотелось набрать на каждый лист карты максимально возможное количество точек, а их катастрофически не хватало, особенно в таких задачах, как привязка военно-топографической трехверстной карты. Ведь часто бывает, что на одном листе есть всего лишь два-три пересечения параллели с меридианами, а значит и точно определены две или три точки. Собственно это и послужило стимулом создания калькулятора, упомянутого выше, поскольку уже тогда было точное понимание того, что для привязки следует использовать только «служебную» информацию: линии градусной сетки и рамку собственно карты, поскольку все остальные изображенные на карте объекты вторичны по отношению к ней. Набор и расчет такого количества точек на каждый лист всегда занимает большую часть времени.

Второе вытекает из первого — и тут мной была допущена та же самая ошибка, о которой я писал выше: поскольку контрольных точек набиралось много, для трансформации растра в ходе привязки всегда использовался полиномиальный метод. А он, как я уже коротко сказал выше, и как мы с вами подробнее увидим в дальнейшем, всегда сопровождается нежелательными деформациями исходной картинки. Возможно, что из-за этого таким методом не удалось собирать отдельные листы карты в цельное покрытие «без разрывов и нахлестов». Рамка карты иногда получалась не совсем точно совпадающей с теоретически построенной прямоугольной сеткой проекции, пример такого несовпадения, взятый из упомянутой выше статьи, приведен на рисунке ниже.

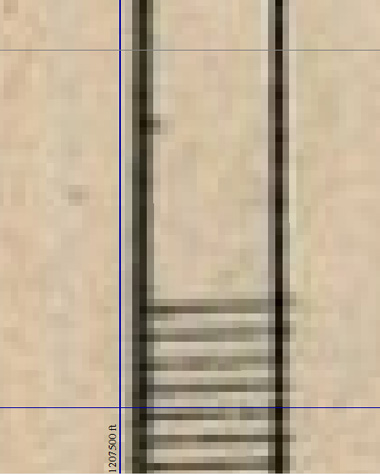
Ясно, что большей частью речь шла о единицах пикселей таких разрывов и других нестыковок, однако же все это сказывалось на общей аккуратности и точности работы.

Наконец, для работы почти всегда использовалось проприетарное программное обеспечение (Spotlight Pro для предварительной коррекции растров, Global Mapper для работы с картами и собственно привязки и т.д.). Понятно, что все это сказывалось и на доступности методик любому желающему. А свободное программное обеспечение делало в те годы лишь первые шаги.

Однако с тех пор прошло достаточно много времени, чтобы переосмыслить всю наработанную за многие годы информацию и попробовать предложить другие методики, которые были бы доступнее, проще в выполнении и точнее всего того, что изложено выше. Тем более, что интерес к поднятым проблемам не угас и не угаснет еще очень долго.

И подводя итог вводной части, следует обязательно подчеркнуть: как вы скоро увидите, никаких сколько-нибудь существенных открытий мы с вами делать не будем. Многие вещи хорошо известны и проработаны уже в течение многих лет.

Однако сколько-нибудь систематического применения и изложения этого применения, как мне представляется, ранее сделано не было. К ним мы и приступим в следующей части.

Литература и примечания

1. В этой части все же появятся несколько терминов. Совсем без терминологии во введении не обойтись, но поскольку это все же введение, определений я им здесь давать не буду, отложив это, как было сказано, до теоретической части. А для удобства чтения выделю их курсивом, чтобы при желании читатель, вдруг решивший вернуться к общему обсуждению, легко мог их найти.

2. «Атлас географический», Большая Российская Энциклопедия 2004-2017 (научно-образовательный портал, старая версия), см. также Берлянт А.М., Востокова А.В., Кравцова В.И., Лурье И.К., Сваткова Т.Г., Серапинас Б.Б. Картоведение, М., 2003, с.19.

3. Чуть выше речь шла о многолистовых картах. Здесь я снова пошел по пути сокращения заголовка: на самом деле в качестве исходных материалов для работы мы будем рассматривать и собственно многолистовые карты, и атласы, но поскольку речь в дальнейшем идет о работе с ними, как с электронными копиями, различиями можно будет пренебречь и, в обычном приближении, называть все «многолистовыми картами». Разделять исходные, «бумажные» объекты на карты и атласы мы будем лишь по необходимости, когда этого потребует контекст изложения.

4. Методы обработки и совместного представления архивных и современных карт. Параллель Менде: Статьи и материалы. /Под ред. Щекотилова В.Г., - Тверь: Изд-во М.Батасовой, 2010.

5. Лазарев О.Е., Лазарева О.С., Шалаева М.В., Щекотилова С.Н., Щекотилов В.Г. Метод использования крупномасштабных топографических межевых карт губерний съемки А.И. Менде в ГИС и геопорталах, Изв. РГО, 2017, т. 149, вып. 2, с.54.

6. Щекотилов В.Г., Лазарев О.Е., Щекотилов А.В. Электронный атлас по крупномасштабным картам XIX в. для Тверской и сопредельных губерний, Геодезия и картография, 2010, №3, с.23.

7. Хотя все, или по крайней мере, большинство этих данных были им совершенно точно известны.

8. Лазарев О,Е., Щекотилов В.Г. Регистрация растровой электронной карты в ГИС с сохранением преобразование подобия, Вестник ТвГУ, серия «География и геоэкология», 2008, вып. 22(82), с.116.

9. Подробно я на этом остановлюсь в теоретической части.

10. Слово «некоторой» станет понятно чуть ниже.

11. Щекотилов В.Г., Шалаева М.В. Формирование комплекса информационных ресурсов по архивным картам поволжских губерний съемки А.И. Менде, Труды 16-й всероссийской научной конференции «Электронные библиотеки: перспективные методы и технологии, электронные коллекции» — RCDL-2014, Дубна, Россия, 13-16 октября 2014 г., с. 267.

12. Напомню, что авторы для проведения основных работ использовали доступные на тот момент материалы, выложенные в сети. А большинство таких доступных сканов были получены на малоформатных сканерах, и каждый лист карты мог представлять собой от двух до шести или даже восьми отдельных изображений. То есть, авторы буквально собирали «паззл» из таких исходников!

13. Голубинский А.А., Лазарев О.Е., Шалаева М.В., Щекотилов А.В., Щекотилов В.Г. Создание комплекса электронных карт по одноверстной топографической межевой карте Нижегородской губернии съемки А.И. Менде, Геодезия и картография, 2014, № 11, с.43.

14. Так, в цитированном выше сборнике [4] на с.125 авторы употребляют оборот «по характерным ориентирам», но далее нигде эту мысль не развивают.

15. Щекотилов В.Г, Бугрова Н.И., Щекотилова М.В. Создание комплекса растровых электронных карт по трехверстной военно-топографической карте Европейской России, Вестник ТвГУ, серия «География и геоэкология», 2011, вып. 1(9), с.125.

16. Шалаева М.В., Щекотилов В.Г. Крупномасштабные архивные карты губерний и территорий России XIX в. как базовый информационный ресурс исследований различной направленности, «Историческая информатика», Алтайский государственный университет, 2013, вып. 1, с.17.

17. Подробнее об этом можно почитать в недавней статье, там же приведен метод независимого подтверждения опубликованных исторических данных по такого рода размерам.

18. Привязка исторических карт. Часть I, теоретическая. Необходимые шаги. // Привязка исторических карт. Часть II, практическая. Привязываем трёхвёрстки.

19. Калькулятор координат листов трехверстной военной топографической карты.