Возвращаясь к «истинному» размеру листов военно-топографической трехверстной карты

В одной из частей «Параллели Тучкова» в одном из примечаний я пообещал решить еще одну «литературную загадку», связанную с военно-топографической трехверстной картой. Эта загадка почти в точности воспроизводит историю со значением широты главной параллели карты, но на этот раз она связана с точными размерами листов карты.

Первое упоминание о таком размере мы встречаем в базовом документе о создании карты: опубликованном в [1] «Высочайшем одобрении проекта о составлении новой военно-топографической карты России», в котором мы встречаем размер в 23 на 16.5 дюйма.

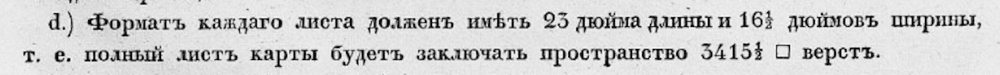
Далее эти же величины мы встречаем в «Каталоге тригонометрических и астрономических пунктов...» И.Ф. Бларамберга (1863 г.) [2], «Историческом очерке деятельности КВТ» за 1872 г. [3], «Сведениях о проекциях карт...» К.В. Шарнгорста (1886 г.) [4] — и вплоть до середины XX в., когда эти же размеры были упомянуты в известном учебнике К.А. Салищева [5].

Однако на рубеже XIX и XX веков появляется вторая группа вполне авторитетных источников, в которых указаны и иные размеры «трехверстки», а именно 22.5 на 16 дюймов. Так, эти величины приведены в известейших учебниках В.В. Витковского [6] и С.М. Соловьева [7], по которым учились целые поколения геодезистов, а также в историческом очерке П. Воларовича в книге Г. Зондервана [8].

Вопрос точного знания размеров листов (а точнее — рамок листов) военно-топографической трехверстной карты представляется мне очень важным. Достаточно тут упомянуть, что эти размеры (также говоря более точно — размеры того прямоугольника на местности, который с учетом масштаба представляет каждый лист) использовался мной в калькуляторе координат листов карты. А в работах В.Г. Щекотилова и сотр. [9] эти размеры вообще являются «краеугольным камнем», поскольку определяют «эквидистантные сетки», по которым осуществляется дальнейшая привязка листов карт.

Данные по размерам листов военно-топографической трехверстной карты (опять же, если говорить точнее — размеры прямоугольника на местности) приведены В.Г. Щекотиловым и сотр., например, в работе [10]. Следует иметь в виду, что эти данные — расчетные и получены решением определенной оптимизационной задачи уже в процессе привязки карты. Именно поэтому авторы всегда приводят интересующие их размеры «на местности», а исходный размер листов не приводят. Кроме того, при таких преобразованиях и расчетах (если они корректны) всегда происходит «подгонка» размеров листов под тот размер, которые они должны иметь теоретически, без учета их деформаций в процессе хранения и погрешностей сканирования. Тем не менее, простой пересчет полученных в [10] данных из метров на местности в дюймы карты дает «теоретические» размеры в 23.07 на 16,53 дюйма, причем эти расчеты основаны на 524 листах «трехверстки».

Более прямые измерения, сделанные мной в 2012 г. с помощью программы Spotlight Pro, показали, что ширины и высоты листов «меньше литературных значений на несколько десятых дюйма», однако в то время данные по второй группе размеров (22.5 на 16 дюйма) были мне неизвестны, что и позволило сделать вывод о том, что эти предварительные измерения в целом подтверждают размер в 23 на 16.5 и косвенные расчеты В.Г. Щекотилова с сотр.

Со времени тех пробных измерений прошло уже много времени, и теперь нам с вами известен, как минимум, еще один массовый вариант размеров. Кроме того, из изложенного в «Параллели Тучкова» следует, что мнение большинства, приведенное в источниках, какими бы авторитетными они не были, не всегда правильно, особенно если речь идет о специфических параметрах карт. Все это заставляет такие параметры проверять, и желательно, независимыми методами.

Но исходные данные по размерам военно-топографической карты у нас с вами уже есть. В одной из частей «Параллели Тучкова» я акцентировал ваше внимание на том, как измерять углы наклона параллелей к горизонтальным рамкам карты, но при этом мы с вами измерили и сами размеры этих рамок! Пришло время воспользоваться результатами этих измерений и решить вопрос: сможем ли мы сделать выбор в пользу одного из известных литературных вариантов.

Однако, прежде чем мы с вами займемся обработкой данных, давайте сделаем небольшое отклонение в неожиданную сторону: специфические области химии и технологии. Это нам поможет понять, какие результаты нам с вами следует ожидать.

Начнем совсем издалека. Военно-топографическая карта, как известно, напечатана на бумаге, а бумага, как может быть вы помните из школы, состоит из целлюлозы. Целлюлоза — это такой природный полимер, который добывают из самых разнообразных растительных источников сырья. Самое важное, что нужно знать — это то, что молекулы целлюлозы представляют собой очень длинные цепочки, которые в процессе изготовления бумаги собираются в вытянутые волокна, которые в свою очередь обладают способностью скрепляться друг с другом (с помощью связей разнообразного вида) с образованием достаточно прочной структуры. Эта структура после ряда технологических процессов, в детали которых мы с вами вдаваться не будем, и образует привычную нам бумагу.

Теперь давайте зафиксируем для понимания следующее: с течением времени технологии изготовления бумаги сильно менялись. Настоящая революция произошла как раз в середине XIX в., когда на смену более дорогой бумаге, изготовленной из хлопкового или льняного сырья, пришла более дешевая, для которой сырьем служила (и служит сейчас) обычная древесина. Это привело к существенному удешевлению печати, однако в целом — к ухудшению «среднего» качества бумаги. Такой переход повсеместно произошел во второй половине XIX в. [11]. А с переходом в дальнейшем от печати карт с гравированных медных листов к офсетной печати качество еще больше ухудшается, поскольку изменяются и технологические требования для такой печати.  Запомним эти факты, они нам пригодятся в дальнейшем обсуждении.

Ухудшение качества, о котором идет речь, связано не только с сиюминутными характеристиками бумаги. Изменение характеристик во времени известно как «старение бумаги». Химической подоплекой таких процессов является, в первую очередь, изменение степени скрепления волокон целлюлозы, о котором говорилось выше, например, появляется большее количество поперечных сшивок между вытянутыми молекулами целлюлозы. В основном это происходит под действием остаточных реагентов в листе бумаги, которые использовались в процессе ее изготовления (именно поэтому «древесная» бумага стареет быстрее, чем более старая по времени изготовления бумага из хлопкового сырья). Ясно, что такой процесс сказывается на визуальных (бумага желтеет) и прочностных (бумага становится более хрупкой) характеристиках. Но это не все, есть еще один процесс, который свойственен буквально всем видам бумаги: потеря остаточной воды, которая в ней содержится как в свободном, так и в связанном виде. Как и чисто химические процессы, это ведет к изменению визуальных и прочностных характеристик, а также — и это очень важно —к изменению физических размеров листов бумаги. Бумага усыхает со временем, или, как говорят профессионалы, «усаживается».

Сам термин «усадка» чаще всего используют в контексте процесса непосредственного изготовления бумаги [12], когда свежеизготовленная бумага теряет основную массу воды, и для его контроля зачастую приходится применять отдельные усилия. Однако надо иметь в виду, что этот процесс протекает и в дальнейшем, в процессе хранения, хотя и в меньшей степени. Также очень важно понимать, что процесс в целом необратим. Несмотря на то, что при поглощении воды (например, при намокании, или просто при увеличении влажности) размер бумажного листа немного увеличивается за счет проникновения молекул воды между волокнами, при обратной потере воды (при высыхании или возврате окружающей среды к прежней влажности) размеры листа никогда не возвращаются к предыдущим размерам, а становятся меньшими. Такое явление называется «остаточной деформацией» [13]. Интересно также, что величина такой деформации часто различна для разных направлений листа — продольного или поперечного [14]. В свою очередь, это связано с тем, что волокна целлюлозы, о которых шла речь выше, преимущественно ориентированы в одном из направлений листа, по крайней мере, для определенных технологий изготовления.

Сказанное выше подводит нас с вами к пониманию того, что многократное изменение окружающей влажности, а также неостановимые химические процессы внутри бумажного листа приводят к заметным изменениям его размеров при хранении, причем во-первых, в сторону уменьшения, а во-вторых, достаточно независимо для его ширины и высоты.

Между тем, подробное изучение процессов, происходящих при старении бумаги началось лишь ближе к 60-м годам XX в. [11], и только после этого пришло понимание того, что для хранения бумажных архивных документов необходимо принимать специальные меры (в том числе и поддержание постоянной влажности), и это понимание стало оформляться в виде нормативных документов.

Таким образом, мы с вами могли бы, еще до всяких измерений и их обработки, вполне обоснованно предположить, что измеренные ширины и высоты листов карт (их внутренних рамок) окажутся в среднем меньше, чем их предполагаемые, исходные, «теоретические» величины (23 на 16.5 или 22.5 на 16 дюймов). Весь вопрос — насколько меньше и сможем ли мы различить эти два варианта?

ПОДГОТОВКА ИСХОДНЫХ ДАННЫХ

Напомню, что когда в «Параллели Тучкова» мы с вами работали над определением широты главной параллели «трехверстки» и использовали для этого углы наклона параллелей, исходным материалом для этого служили сканы польского проекта mapiwig.org (сами сканы размещены на дочернем проекте Mapster). Исходные данные для расчетов были сведены в файл TP.xlsx. Они находятся на самом первом листе «Геометрия листов». Поскольку тогда нас интересовали измеренные углы наклона, на остальной части я остановился лишь бегло. Теперь пришло время заняться ею более подробно. Как вы помните или видите в открытой вами таблице, попутно с измерением углов, я померил ширины и высоты листов (в таблице они приведены в пикселях для всех четырех сторон рамки измеряемой карты). А заодно я рассчитал средние (по двум измерениям) значения ширин и высот в дюймах (это легко сделать, поскольку известно разрешение каждого растра в пикселях на дюйм).

Для дальнейших расчетов мы с вами будем пользоваться именно этими последними, усредненными данными. Правда, говоря строго статистически, мы с вами потеряем часть информации, а именно ту, которая нам говорит о «непрямоугольности» листа карты, которая могла получиться из-за неравномерной деформации листа по причинам, которые мы с вами обсудили чуть выше или из-за погрешностей при изображении, печати и т.д. Однако таковая «непрямоугольность» в целом незначительна по сравнению с теми эффектами, которые мы сейчас обнаружим, поэтому для удобства мы ей  пренебрежем. Тем не менее, любой желающий может легко повторить тот расчет, которым мы с вами скоро займемся, и вполне самостоятельно — на полном наборе ширин и высот.

При таком усреднении есть и довольно заметный «плюс». Эта предварительная операция немного уменьшит стандартное отклонение значений ширин и высот по сравнению с исходными, неусредненными данными и в конечном итоге позволит поточнее определить средние ширины и высоты для всей выборки. Почему так происходит, хорошо разобрано в уже не раз рекомендованном и цитированном мной учебнике [15], здесь лишь еще раз подчеркну, что так мы слегка упрощаем нашу модель, считая лист строго прямоугольным.

Последнее, что я хочу добавить перед тем, как мы займемся расчетами, это то, что вести мы их будем, как и раньше с использованием пакета RStudio, работа с которым подробно освещалась в одной из частей «Параллели».

Давайте еще раз загрузим, как это было описано в упомянутой части, Excel-файл с исходными данными. Однако теперь нам потребуется не лист с измеренными углами наклона, а самые первичные данные — первый лист, который называется «Геометрия листов». Напомню, что для этого командой library() у нас должен быть подключен пакет readxl.

На этом этапе мы загружаем всю электронную таблицу целиком, так немного проще, а нужные данные мы с вами выберем на дальнейших шагах.

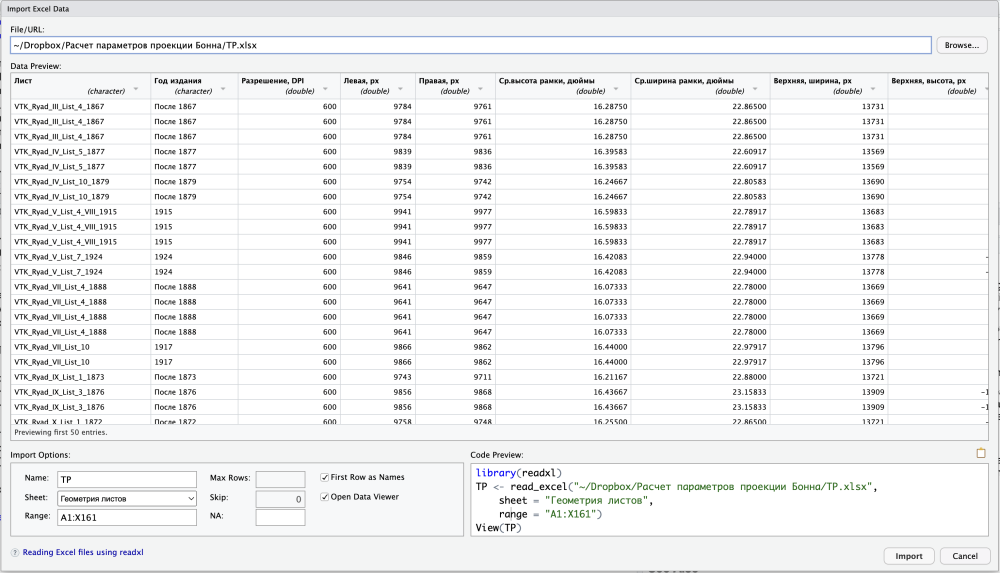
Как вы хорошо помните, полностью отобразить таблицу можно командой View(TP) (и тогда она будет показана в верхнем левом окне над консолью), а также просто напечатав «TP» (и тогда она будет показана в консоли в виде тиббла).

Теперь нам нужно, чтобы таблица содержала лишь необходимые для дальнейшей работы данные. Пока же мы видим, что данные довольно сырые, например, содержат множество лишних колонок, колонки имеют длинные, неудобные для работы названия, а строки с одним и тем же листом и одними и теми же значениями ширины и высоты встречаются по столько раз, сколько нам надо было измерить углов на листе в предыдущих измерениях.

Для удобной работы с табличными данными в R есть специальный пакет, который называется dplyr. Вообще говоря, этот пакет является частью огромного «пакета с пакетами» или библиотеки tidyverse, однако всю целиком мы ее устанавливать не будем, она нам не нужна, а вот dplyr установим уже привычным для нас способом, скачав его из репозитория CRAN.

После установки пакета его, как вы также хорошо помните, следует подключить к текущей сессии командой library().

А вот дальше мы с вами займемся магией, которая обусловлена, во-первых, возможностями современных версий языка R, а во-вторых, возможностями только что установленного пакета. Как вы помните из упомянутой статьи, последовательные операции над данными мы с вами совершали или последовательными отдельными командами (каждый раз сохраняя промежуточные данные в переменные), или нам приходилось использовать множество «вложенных скобок», если мы хотели выполнить несколько операций за один раз.

Сейчас я покажу, как получить необходимую нам таблицу, с которой будет уже удобно работать буквально одной командой. И в этом нам поможет концепция «пайпов» (pipes), которая в последних версиях языка встроена в базовый пакет [16].

Концепция пайпов очень проста: исходный объект или результат предыдущей операции над объектом подается «на вход» следующей операции. Таким образом, последовательность операций над исходным объектом записывается в естественном виде — слева направо, в порядке их выполнения. Та же запись последовательности операций в «классическом виде», с вложенными скобками, всегда требует чтения справа налево, поскольку и объект, и самая первая операция, вложены в эти скобки наиболее глубоко.

Итак, давайте подадим следующую команду, а то, что в ней записано, я разберу ниже.

В самой левой части у нас стоит знакомый оператор присвоения <-, который присваивает переменной dim результат работы всей правой части выражения. Дело в том, что при выполнении пайпов никак не модифицируются исходные данные, а полученный результат просто отображается в консоли. Нам же нужно сохранить измененную таблицу для дальнейших расчетов.

Итак, на вход пайпов подается переменная TP, то есть тот тиббл или таблица, который мы с вами получили выше, прочитав Excel-таблицу. Далее этот тиббл обрабатывается функцией select() пакета dplyr, выбирая нужные нам колонки (первую, шестую и седьмую). Обратите внимание, что при записи через пайпы указание самого первого параметра функции, в виде select(TP, ...), не нужно, поскольку он однозначно определен тем, что написано слева от значка пайпа.

Далее из общего массива данных мы выбросим три строчки. Это обусловлено тем, что первая из этих строк относится к скану, у которого обрезаны боковые стороны вместе с боковыми сторонами измеряемой рамки, а две оставшиеся — к карте, имеющей заметные разрывы по всему полю. Измерению углов наклона, как я посчитал ранее, это не помешало, а вот для измерения размеров рамки это, конечно, критично. Итак, такое удаление делается функцией slice() того же пакета.

Теперь, поскольку мы удалили для каждого отдельного листа карты все столбцы с измеренными углами, все строки с оставшимися размерами листов становятся полностью идентичными для каждого листа. И их можно сгруппировать вместе, используя функцию group_by(), но чтобы таблица при этом сохранила данные по ширинам и высотам, нам нужно объяснить R, что при такой группировке нужно делать с повторяющимися в каждой группе значениями этих столбцов, а для этого служит функция summarise(), применяемая к этим столбцам. Поскольку для каждого листа карты эти данные в оставшейся таблице идентичны, здесь можно применить множество вариантов (среднее значение, медиану, любое порядковое значение). Поступим самым простым способом: возьмем в каждой группе первые (first()) значения для ширины и для высоты.

В получающейся последовательным движением по пайпам таблице столбцы получат еще более длинные названия вроде 'first(Ср. ширина рамки, дюймы)', поэтому на последнем этапе переименуем их в короткие, но тем не менее, понятные названия 'width' и 'hight'. Как вы уже догадались, это делается функцией rename().

Теперь посмотрим, что у нас с вами получилось, например, с помощью функции View(dim). Как видим, мы получили желаемый результат, с которым уже удобно работать: для каждого отдельного листа карты мы оставили лишь по одному значению ширины и высоты и удалили ненужные нам столбцы.

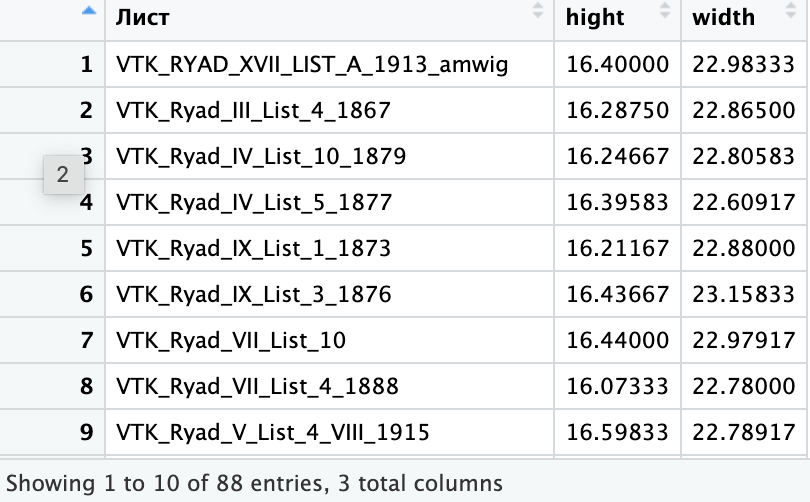
Теперь полученную таблицу можно сохранить в новый файл, чтобы легко использовать в дальнейших расчетах. Как вы помните, это делается командой saveRDS().

РАСЧЕТЫ

Вот теперь у нас с вами все готово для дальнейших расчетов. Давайте вначале посмотрим, как в графической интерпретации выглядят наши данные по ширинам и высотам. Как я уже показывал ранее, проще и нагляднее всего это сделать, построив гистограмму.

Полностью текст статьи вы можете прочитать, посетив страницу автора на Boosty.