Объединенные электронные атласы из многолистовых крупномасштабных карт XIX-XX веков. Теоретический минимум. Часть вторая.

В предыдущей части мы с вами уже столкнулись с координатами — когда обсуждали, какие есть способы позиционирования некоторого изображения (растрового или векторного) на реальной поверхности Земли. Мы использовали понятия широты и долготы и назвали эти координаты географическими, не вдаваясь в дополнительные подробности. Давайте теперь эти подробности рассмотрим внимательнее, а заодно раз и навсегда определимся с терминологией, которой мы будем придерживаться в дальнейшем изложении.

Здесь нам придется пойти вполне стандартным путем и коротко напомнить, какие приближения для модели Земли существуют и где они используются. Из понимания этого будет следовать понимание и всех остальных вещей: терминов, связанных с координатами, систем координат, их преобразований и прочей работы с ними.

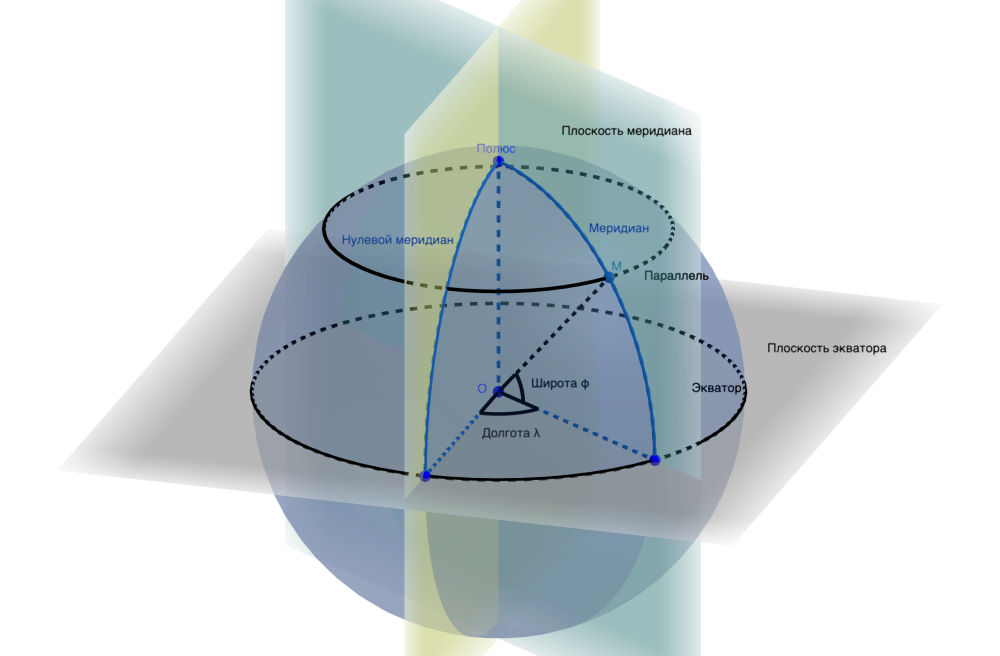
Итак, мы с вами помним, что реальную сложную форму Земли в самом первом и грубом приближении можно представить в виде шара, а ее поверхность, соответственно — в виде сферы. У этой сферы есть два полюса, через которые проходит земная ось (воображаемая линия, вокруг которой Земля вращается) и линия-окружность, равноудаленная от этих полюсов, которая называется экватор. Тогда для того, чтобы точно определить положение какой-то точки на этой сфере, можно указать две величины. Первая — это угол между плоскостью экватора и направлением на эту точку, проведенным из центра нашей сферы. Этот угол называется широтой точки (на рисунке ниже обозначена буквой φ). А окружность, проведенная через эту точку параллельно плоскости экватора, будет называться параллелью. Теперь, если мы проведем окружность через оба полюса и эту или некоторую другую точку, мы получим линии меридианов. Двугранный угол, образованный этими линиями и осью вращения Земли даст нам разность долгот этих двух точек. А если мы выберем какой-то определенный меридиан в качестве начала отсчета и присвоим ему значение нулевой долготы, то разности долгот, отсчитанные от этого «нулевого» (или «начального») меридиана превратятся просто в долготы относительно этого меридиана (на рисунке долгота обозначена буквой λ).

Теперь перейдем к следующему по сложности и самому распространенному приближению: представлению формы Земли в виде эллипсоида вращения (эллипсоид вращения еще называют сфероидом). Такое представление возникает из того факта, что Земля вращается вокруг своей оси, при этом центробежные силы слегка растягивают первоначальную сферу в области экватора (а в районе полюсов Земля слегка сжимается, ведь суммарный объем фигуры остается постоянным). Основными параметрами, которые характеризуют любой сфероид, является его большая полуось a, направленная в сторону экватора и малая полуось b, направленная в сторону полюса, а также параметр, который связывает между собой размеры большой и малой полуосей и называется сжатием f = (a - b) / a.

Чем больше величина разности большой и малой полуосей, тем больше сжатие f. Для наглядности этот параметр часто записывают в виде «сокращенной дроби», например 1:298.26. Также часто используют величину знаменателя этой дроби, которую называют «обратным сжатием». Типичные величины этого обратного сжатия для различных моделей земного эллипсоида лежат в области, близкой к 300, чем больше эта величина, тем меньше сжат сфероид (и тем ближе он к сфере). Из формулы очевидно, что большая, малая полуось и сжатие связаны однозначным соответствием, поэтому, чтобы описать сфероид, достаточно указать любые два из трех его параметров. Чаще всего используют большую полуось и сжатие (или обратное сжатие).

Мы с вами видим, что величина сжатия представляет собой довольно малую величину (то есть, разность большой и малой полуоси по отношению к размеру большой полуоси составляет приблизительно 0.3%). Однако, этого вполне достаточно, чтобы в масштабах Земли в совершенно явном виде проявился вопрос: «а как нам правильно определить широту для эллипсоида»? Можно спросить и так: «а какой угол нам следует измерять»?

Существует два способа определения такого угла. Если мы на минутку вернемся к рисунку определения широты на сфере, то увидим, что угол (и широту) мы определяли, как угол между плоскостью экватора и радиусом, проведенным из центра сферы. В то же время, направление этого радиуса для сферы совпадает с так называемой нормалью к этой сфере в определяемой точке [1]. Что же, широту для точки и на сфероиде определяют в большинстве случаев точно так же: как угол между нормалью к поверхности эллипсоида (сфероида) и плоскостью экватора, и называют ее географической широтой. Как мы с вами видим из рисунка ниже, на котором сжатие сфероида для наглядности очень сильно преувеличено, этот угол (обозначенный, как это обычно принято, буквой B) немного не совпадает с углом φ, вершина которого лежит в точности в центре сфероида. Используют ли где-то этой второй угол? Ответ — да, но обычно в различных промежуточных, вспомогательных вычислениях, при этом он все же имеет свое название: геоцентрическая широта. Впрочем, другое применение геоцентрических координат мы с вами увидим немного позже.

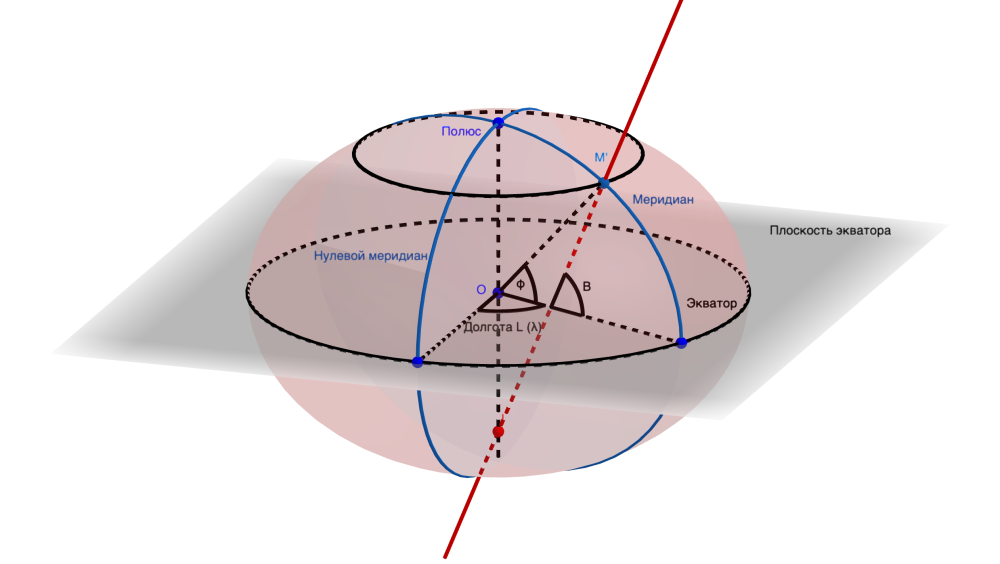
Если мы учтем то, что «вид сверху» на наш сфероид представляет собой окружность, точно так же, как и для сферы, станет понятно, что определение долготы, как двугранного угла между меридианом, проведенным через точку и некоторым выбранным меридианом (на сфероиде ее обычно обозначают буквой L), у нас не изменится. И все вместе мы назовем географическими координатами точки на эллипсоиде.

Давайте теперь сразу разберемся, почему для определения географической широты на сфероиде используют более сложный метод с нормалью, а не считают ее, как на сфере, из центра эллипсоида. Дело в том, что до сих пор мы считали себя географами, точнее — картографами и использовали в своих построениях несколько идеализированную картину мира в виде идеального же «математического» эллипсоида, который, к тому же, нам кто-то задал. Но есть еще огромная группа, которая связана с более реальными измерениями на местности. Эта группа называется «геодезисты». Так вот, в практической геодезии нет никакого «центра эллипсоида» или «нормали к касательной плоскости в точке». Все, чем оперирует практическая геодезия — это направление так называемой «отвесной линии», по этому направлению устанавливаются все их измерительные приборы. Вообще говоря, эта линия должна была бы быть направлена строго в центр масс нашей фигуры Земли из-за ее тяготения, при этом не имеет значения, представляем ли мы ее сферой или сфероидом. Но это только в том случае, если Земля покоится. Но мы знаем, что она вращается вокруг собственной оси! Легко понять, что практически в каждой точке (кроме полюсов и экватора) из-за такого вращения на любое тело, в том числе и отвес, будет действовать центробежная сила, которая будет отклонять отвес от направления к центру Земли (причем, наружу) [2]. Так вот, для вращающегося сфероида для любой точки равнодействующая двух этих сил (притяжения к центру масс и центробежной силы) направлена в точности перпендикулярно касательной плоскости к поверхности сфероида. А это значит, что направление отвеса и нормали совпадают (с точностью до абсолютного направления [3])!

Почему же так получается? Все дело в том, что первично вращение сфероида вокруг оси, именно его скорость определяет ту силу, которая действует на любую точку на поверхности или внутри сфероида, и нет разницы, на что она действует — на отвес или любую точку самого сфероида, заставляя деформироваться его описанным выше способом. И если бы наш вращающийся сфероид был идеальным (лучше всего, жидким, чтобы ничего не мешало деформациям, и к тому же имел бы везде одинаковую плотность), то его форма уравновесилась бы при вращении ровно таким образом, чтобы любая отвесная линия в любой точке совпадала по направлению с нормалью к поверхности сфероида.

Вот именно поэтому такое определение широты через отвесную линию называют еще геодезической широтой, но для сферы и идеального сфероида, как мы с вами видим, они совпадают с географической широтой. Определение же геодезической долготы (через двугранный угол, как мы это сделали выше) ничем не отличается от определения географической долготы. Но все вместе мы назовем теперь геодезическими координатами.

Таким образом, пока мы живем в мире идеального сфероида, нам нет нужды как-то различать географические и геодезические координаты, разница в терминологии отражает лишь способ определения координат. Но все усложняется, когда мы переходим в жизнь реальных геодезистов. И здесь мы с вами подошли к следующему уровню усложнения модели Земли — геоиду [4].

Выше мы уже видели, что точное совпадение направления нормали («перпендикуляра») к поверхности и отвесной линии возможно только лишь для свободно деформируемого (например, полностью жидкого) вращающегося небесного тела. Но ведь Земля не такова, и геодезисты это хорошо знают. Во-первых, примерно треть ее занята сушей, которая, к тому же, имеет свой сложный рельеф с горами и впадинами. Во-вторых, само внутреннее строение планеты с ядром, мантией и твердой корой далеко от такой свободно деформируемой модели. И наконец, само распределение масс внутри планеты заметно неравномерно. Все это приводит к тому, что во-первых, сама форма Земли отклоняется от идеального сфероида, хотя и за миллиарды лет своего существования приняла форму, довольно близкую к сфероиду. Во-вторых, из-за неравномерности распределения масс отвесная линия в каждой точке планеты может отклоняться от направления, «предписанного» моделью идеального сфероида. Геодезисты это явление хорошо знают и называют «уклонением отвесной линии». Как же поступают в таком случае?

А в таком случае договорились считать, что любой малый участок поверхности фигуры Земли в выбранной точке перпендикулярен направлению отвесной линии в этой точке [5]. Все это приводит к тому, что форма земной поверхности теперь будет представлена не идеальным сфероидом, а сложной фигурой, в которой есть выступы и впадины. Ее и называют геоидом, и именно с такой фигурой работают геодезисты. Схематичное изображение фрагмента такой фигуры приведено на рисунке ниже, где черной линией показана поверхность геоида, зеленой штриховой — поверхность сфероида, а также проведены нормали к сфероиду и геоиду, иллюстрирующие уклонения отвесных линий.

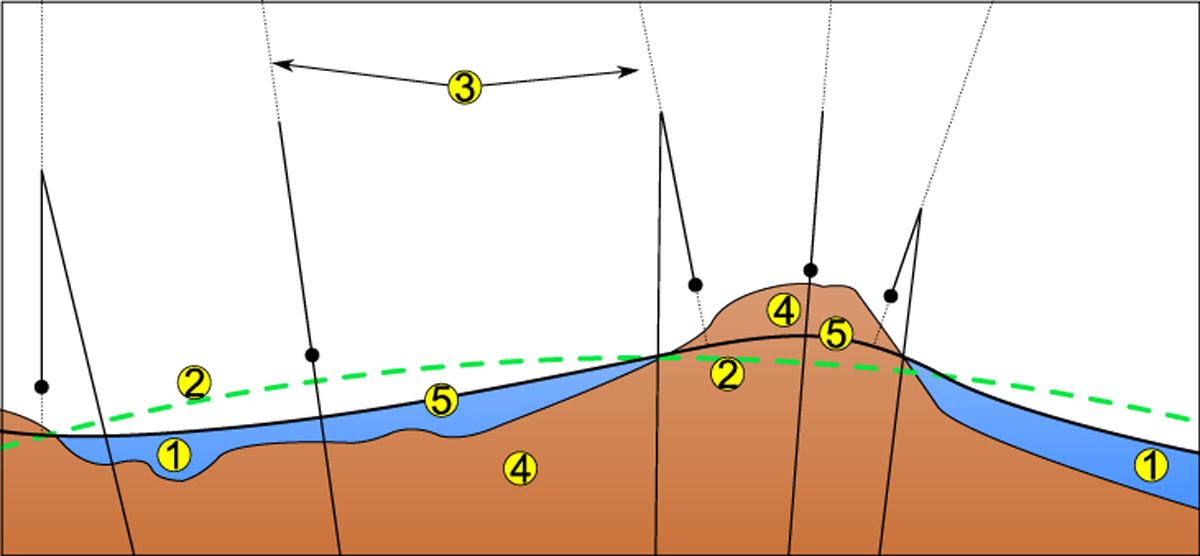
Стоит подчеркнуть, что эта фигура — умозрительная, можно сказать вымышленная, и не соответствует реальной поверхности реальной Земли. На поверхности морей и океанов она в целом совпадает с невозмущенной водной поверхностью, а вот на суше — как бы сглаживает реальную поверхность. Однако именно она позволяет вести геодезические измерения гораздо более точным образом. Еще один момент стоит повторить: направление нормали к поверхности для любой точки геоида совпадает с направлением отвесной линии просто по определению самого геоида [6].

И вот здесь мы уже получаем различие между координатами на эллипсоиде, определенными «геодезическим» способом через отвесную линию и координатами на геоиде (а они, как мы видим измеряются через отвесную линию по определению). Просто потому, что поверхности эллипсоида и геоида — это разные модели и отвесные линии для них не совпадают из-за «искривления» поверхности геоида. Поэтому разумнее всего оставить название «географические» для модели эллипсоида, а для более точной модели геоида пользоваться названием «геодезические координаты» [7].

Однако есть еще один способ описания реальной земной поверхности, но прежде, чем мы с вами к нему перейдем, я должен сказать, что выше в рассмотрении способов определений координат для простоты изложения я сознательно опустил еще одну координату, поскольку мы рассматривали только лишь поверхности исследуемых фигур Земли (сферы, сфероида или геоида). Что нам делать, чтобы описать реальный рельеф местности? Все очень просто: нужно добавить к угловым величинам (широте и долготе) еще одну величину, измеряемую в единицах длины (например, в метрах), которая будет показывать величину отклонения измеряемой реальной точки от поверхности фигуры приближения (например, сфероида) и назвать ее геодезической высотой H [8]. Таким образом, мы получим уже три координаты, которые однозначно определят положение точки в пространстве (а не только на поверхности).

Но тогда вместо угловых величин координат мы с вами вполне можем везде использовать и линейные, которые будут совпадать с привычными координатами для трехмерного пространства (на рисунке ниже они обозначены X, Y, Z и их величины отмечены отрезками красного цвета). Куда поместить начало отсчета этих координат? По причинам, о которых я скажу совсем скоро, его помещают в центр масс модельной фигуры (например, в геометрический центр сферы или сфероида, на рисунке ниже сами оси координат отмечены отрезками синего цвета). Таким образом, наши новые координаты, с одной стороны, можно назвать геоцентрическими, а с другой стороны — их также часто называют геодезическими, поскольку именно их используют геодезисты в своих промежуточных вычислениях. Однако во избежание путаницы, лучше всего использовать для них термин «картезианские» («cartesian» в английском варианте), что мы с вами в дальнейшем и будем делать [9].

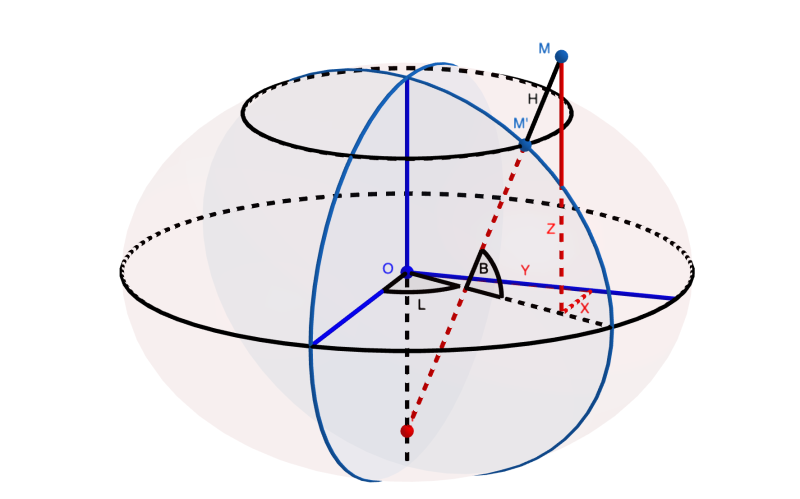
Почему для начала отсчета картезианских координат используют центр модельной фигуры Земли? Во-первых, это самое логичное место по отношению к самой фигуре. Во-вторых, оказывается, что формулы перехода от таких координат к географическим (геодезическим, так как мы их определили выше), где используются угловые единицы, и формулы обратного перехода от географических к картезианским являются довольно простыми [10]. А для еще большей простоты и однозначности связи с географическими координатами одну из осей направляют в полюс, а вторую — в точку пересечения экватора и нулевого меридиана. Наконец, в-третьих, и это, пожалуй, для нас самое главное, такой способ представления используется в расчетах связи пространственных координат, виды которых мы с вами рассмотрели, с еще одним видом координат — координатами проекции. Этот последний вид координат в этой части мы с вами рассматривать не будем, поскольку логичнее всего рассмотреть их вместе с понятием самой «проекции». Здесь лишь уточню, что такие координаты используются при отображении пространственной картины, которую мы с вами изучили выше, на плоскость, то есть фактически — при составлении карт, которые, по сути, и являются предметом нашего основного рассмотрения [11].

Теперь, прежде чем мы перейдем к обстоятельному разговору о новом понятии «система координат», которого я в изложении выше старался всеми силами избегать, ограничиваясь термином «координаты», хотелось бы зафиксировать две очень важные для дальнейшего понимания вещи, связанные с приближенными фигурами Земли, только что изученные нами.

Первое. Для целей картографии, а тем более, картографии XIX-XX вв. вполне достаточно в качестве модели такой фигуры использовать сфероид. Его картографы и используют, а более точная модель геоида используется в целом лишь геодезистами при проведении первичных измерений. Но с этим связан и второй вопрос: как определить, какой эллипсоид (сфероид в подавляющем большинстве случаев) нужно использовать? И как связать его с геоидом, ведь геодезические измерения на геоиде нам надо будет как-то переносить на некий эллипсоид? Какой?

И вот тут решение вопроса становится неоднозначным, поскольку все зависит от поставленных целей. Проще всего, если нам требуется найти такой сфероид, который наилучшим образом приближает реальную форму всей земной поверхности. В качестве такого сфероида выбирают сфероид, центр которого лежит в точности в центре масс геоида, а поверхность — наилучшим образом приближает поверхность всего геоида [12]. Такой эллипсоид (сфероид) называют общеземным.

Следует иметь в виду, что рассчитанные параметры общеземного эллипсоида как «наилучшего приближения» меняются со временем, поскольку всегда уточняются параметры базовой фигуры — геоида. Точнее сказать, менялись, и особенно заметно — в течение всего XIX-го века. В этой части я не буду подробно останавливаться на всех моделях эллипсоидов прошлых лет, по необходимости мы с вами будем их вспоминать по ходу дальнейшего изложения. Разве что стоит упомянуть, что за прошедшие две с лишним сотни лет рассчитанные размеры (например, большая полуось сфероида) выросли примерно на два с половиной километра! В настоящее же время уточнения все же идут, но речь теперь идет о буквально сантиметровых изменениях. Таким образом уже достаточно давно в качестве такого общеземного эллипсоида (и как мы увидим совсем скоро, эталонного) используется эллипсоид WGS84 [13]. Впрочем, есть и альтернативные ему модели, например, разработанный в СССР эллипсоид ПЗ-90, или более поздняя модель IERS 1996 года, однако по сути, речь идет об уточнениях в пределах долей метра, связанных в первую очередь с уточнениями модели геоида, а наилучшее его приближение всегда одно — это и есть общеземной эллипсоид. 

Должен сказать, что для определения того, что такое система географических координат [14] нам остается всего один шаг. Для этого нам нужно всего лишь добавить положение начального меридиана на выбранном сфероиде (общеземном эллипсоиде), от которого мы будем отсчитывать долготу точно так, как мы с вами это делали в самом начале этой части. Этого совершенно достаточно для указания положения любой точки на эллипсоиде [15].

Однако с общеземным эллипсоидом есть одна проблема. Несмотря на то, что он является наилучшим приближением к геоиду в среднем по всей поверхности Земли, для отдельных участков он может быть недостаточно хорош. Поэтому для лучшего приближения этих отдельных участков (например, территорий отдельных государств) предлагают слегка отличающиеся от общеземного модели эллипсоидов. Такие эллипсоиды (сфероиды) называют референц-эллипсоидами и они часто используются для построения карт на территорию той страны, для которой они рассчитаны. В качестве примера такого референц-эллипсоида на территорию бывшего СССР можно привести хорошо известный эллипсоид Красовского, с помощью которого построено множество топографических карт второй половины XX века (впрочем, его часто используют и в наши дни, поскольку в некоторых случаях построения на его основе точнее) [16].

Как связать общеземной эллипсоид с многочисленными вариантами референц-эллипсоидов? Давайте рассмотрим рисунок, который я взял с сайта «Картетика» [17], из которого будет понятен общий принцип и некоторая новая терминология. Чтобы не загромождать чертеж, с него удалены сами контуры эллипсоидов, зато показаны геоцентрические (картезианские) координатные оси, причем для каждого из эллипсоидов, взята собственная система таких координат. Это те же самые оси, которые на предыдущем рисунке были обозначены синим цветом. Точка же P является общей для обоих сфероидов. Тогда можно допустить, что и некоторая ограниченная область вокруг этой точки является довольно близкой для обеих фигур и представляет собой ту территорию, для которой применяется референц-эллипсоид. А для определенности отнесем координаты с индексами «1» к референц-эллипсоиду, а координаты с индексом «2» — к общеземному.

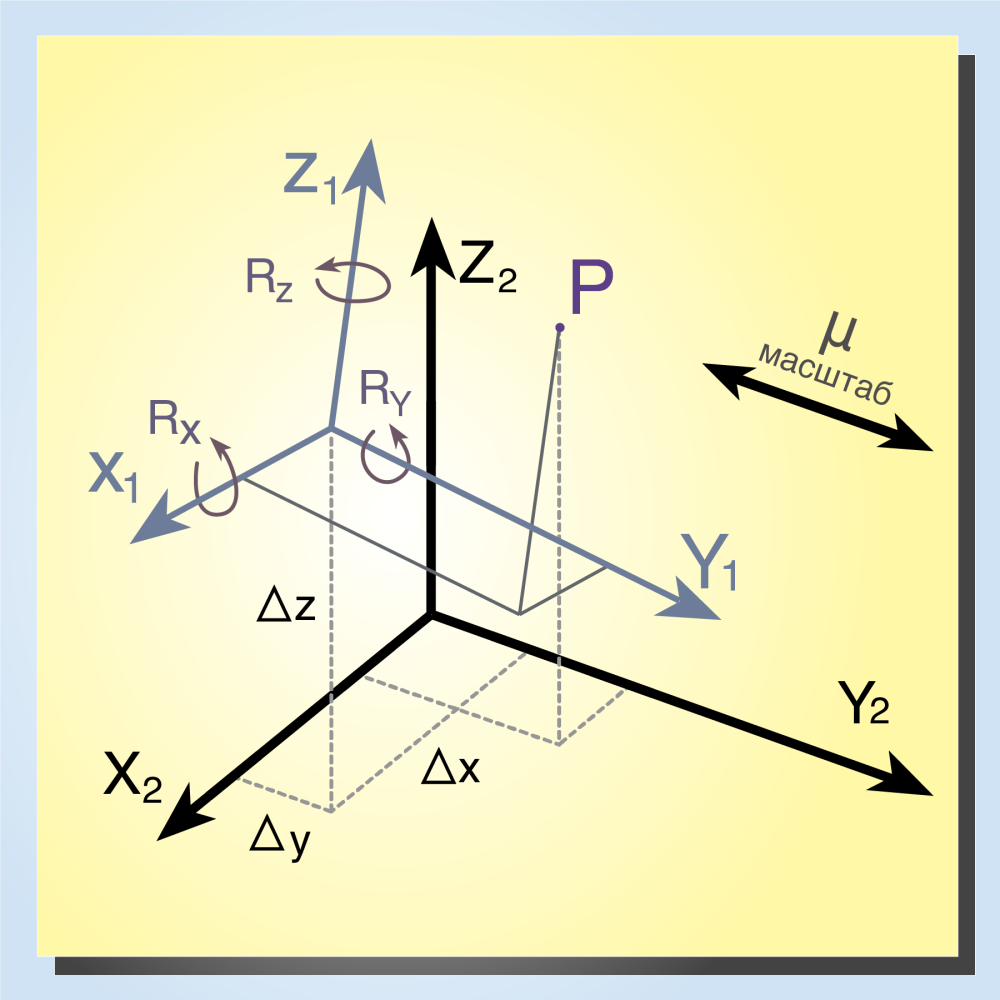
Таким образом, для каждого из двух эллипсоидов мы определили собственную систему картезианских координат. А из рисунка следует, что в общем виде они сдвинуты и повернуты про всем трем осям друг относительно друга (при этом мы с вами помним, что окрестность точки P на референц-эллипсоиде в целом лучше описывает состояние реальной местности по сравнению с окрестностью на общеземном эллипсоиде). Эти сдвиги и повороты также отмечены на рисунке. И вот такое описание эллипсоида вместе с его величинами полуосей (или параметром сжатия), а также с параметрами смещения и поворота относительно общеземного называется датумом. Примеры того, как выглядит описание датума в различных программах я отложу до следующих частей, когда мы наконец полностью закончим с системами координат.

Однако сразу же становится очевидным, что координаты точки на таком «сдвинутом и повернутом» эллипсоиде не будут равны координатам на общеземном эллипсоиде, ведь точка находится на одном и том же месте, а эллипсоид мы двигаем и поворачиваем вместе с его системами координат, как картезианских, так и связанных с ними географических. Как поступают в таком случае, чтобы описание координат было понятным и самое главное, однозначным?

Самое главное, что всегда следует делать — это при указании координат указывать в какой системе координат они получены. Например, 55°30" с.ш., 35°25" в.д. (WGS84). Здесь мы использовали часто встречающийся вариант написания для координат на общеземном эллипсоиде, неявно подразумевающее выбор Гринвичского меридиана в качестве нулевого меридиана. Однако, чтобы такое указание было совершенно явным и однозначным, систему координат лучше написать в более явном виде как EPSG:4326. С такими обозначениями мы с вами познакомимся в следующей части, здесь лишь скажу, что подобным образом записывают стандарт, который включает в себя полное описание системы, в том числе датум и нулевой (начальный) меридиан.

Теперь система географических координат и на референц-эллипсоиде у нас описана полностью, поскольку те самые параметры смещения и поворота относительно общеземного эллипсоида, о которых шла речь выше, мы учли, когда описывали датум.

Наконец, коротко остановимся на том, как технически пересчитываются географические координаты при переходе от одной системы координат к другой. В современной картографии наиболее часто используют так называемое 7-параметрическое преобразование, которое и приведено на рисунке выше: сдвиги по трем осям координат, повороты вокруг трех осей (и еще для точности подгонки добавляют так называемый коэффициент масштабирования, который тоже показан на рисунке и слегка меняет общие размеры эллипсоида). К сожалению, здесь мы снова сталкиваемся с неоднозначностью терминологии. Можно встретить, например, термин «7-параметрическое преобразование Гельмерта», «преобразование Бурса-Вольфа», а в англоязычных вариантах еще и «Coordinate frame rotation» или «Position vector transformation». Ситуация осложняется еще и тем, что речь может идти не об одном и том же преобразовании, а о преобразованиях, которые различаются направлениями вращения по одной или нескольким осям. Понять сразу, о каком точно преобразовании идет речь, не всегда возможно, да нам сейчас это и не нужно, важнее понять сам принцип пересчета координат [18]. А пересчитываются они довольно простым образом. Вначале географические координаты на одном эллипсоиде преобразуются в геоцентрические картезианские координаты. Как уже говорилось, это делается по довольно простым тригонометрическим формулам. Далее полученные таким образом линейные прямоугольные координаты «обрабатывают» по формуле 7-параметрического преобразования. Это также довольно просто, здесь мы в подробности вдаваться не будем, скажу лишь, что фактически все сводится к простой задаче линейной алгебры (умножению матриц). И наконец, полученные новые картезианские координаты, относящиеся уже к другому эллипсоиду, преобразуются в новые географические координаты формулами, обратными тем, которые применяли на первом этапе. Все такие преобразования легко рассчитываются буквально «на лету» современными ГИС.

Для полноты картины остается добавить, что существуют как упрощения, так и усложнения описанной выше модели 7 параметров. Например, можно использовать только 3 сдвига по осям координат и тогда такое упрощенное преобразование называют «преобразованием Молоденского». А в более сложных задачах используют и большее количество параметров, например, если необходимо учесть какие-то изменения базовых параметров во времени. Нам с вами это совершенно точно не понадобится, а изложенного вполне достаточно для понимания того, как определяются координаты в картографии для модели Земли, которой она оперирует — сфероида.

И наконец следует сказать, что любой референц-эллипсоид пусть и не сильно, но все же отличается от общеземного как размерами полуосей a и b, так и формой (то есть, параметром сжатия f). А отличия в форме (сфероид является нелинейной фигурой!) приводят к тому, что совершенно точно совместить в пространстве один эллипсоид с другим путем сдвигов, поворотов и масштабирования, описываемых линейным преобразованием Гельмерта, невозможно. Что же, любая такая модель является приближенной, и это следует всегда помнить.

Итак, мы с вами разобрали то, как в трехмерном мире определяются координаты и их системы для различных моделей Земли. Но мы с вами все же собираемся работать с картами. А карты — не трехмерная, а двумерная вещь. Поэтому в следующей части мы перейдем к обсуждению проекций и всего, что с проекциями связано.

Литература и примечания

1. Не совсем математически правильно, но довольно наглядно представлять себе нормаль, как перпендикуляр к поверхности (в нашем случае, сферы или сфероида). Более грамотно нормаль определяют как перпендикуляр к плоскости, касающейся поверхности в выбранной точке.

2. Полюс и экватор — особые точки. На полюсе центробежная сила отсутствует и отвесная линия направлена в центр масс. На экваторе сила максимальна, но направлена точно противоположно направлению к центру масс. Следовательно, на экваторе отвесная линия также не отклоняется.

3. Нормаль обычно изображают направленной «наружу» эллипсоида, а направление отвесной линии логично изображать «внутрь». Это различие вполне очевидно и обычно понятно из контекста, поэтому чаще мы будем говорить только о «направлении», подразумевая величину угла такого направления.

4. Для простоты изложения я пропущу еще один промежуточный уровень усложнения — трехосный эллипсоид. Это эллипсоид, у которого все три полуоси, определяющие его в пространстве, различны. Такая фигура в картографии, особенно картографии XIX-XX вв. не используется, поэтому знание о ней нам не понадобится. Все же добавлю, что в других областях науки и техники, например, в космонавтике, она играет очень важную роль.

5. Опять же, если формулировать точнее, «для любой точки направление отвесной линии совпадает с нормалью к поверхности в малой окрестности этой точки».

6. Иногда можно встретить утверждение о том, что модель геоида нельзя представить в виде явных математических формул подобно сфере или сфероиду. Это не так, такие формулы есть, и даже на первый взгляд выглядят не слишком сложно. Однако подробное знакомство с ними покажет, что в зависимости от степени точности, они могут содержать от нескольких сотен (модель EGM96) до нескольких миллионов (модель EGM2008) параметров. Конечно, рассмотрение таких моделей выходит за рамки не только этого цикла, но и вообще всей математической картографии.

7. Внимательный читатель уже заметил, что мы заменили теоретическое, умозрительное понятие «нормали к поверхности» более простым и, самое главное, экспериментально определяемым понятием «отвесной линии». Однако за кадром еще остался вопрос о «плоскости экватора» относительно которой мы с вами измеряем все углы: ведь мы никогда не видим эту плоскость и напрямую ничего не можем с ее помощью измерить. Вопрос практических измерений в геодезии выходит за все допустимые рамки нашего исследования, но для понимания терминологии стоит сказать, что расположение такой плоскости можно однозначно определить через направление оси вращения Земли, например, с использованием такой вполне практически определяемой точки на небесной сфере, как так называемый «полюс мира» (это точка, вокруг которой все звезды производят свое видимое вращение). На простых геометрических соотношениях я тут останавливаться не буду, скажу лишь, что широта, определенная таким способом, называется «астрономической», ее можно рассматривать как часть определения геодезической широты и такое измерение является одним из наиболее точных.

8. Должно быть понятно, что эта точка может лежать как над, так и под поверхностью модельной фигуры Земли, поэтому и геодезическая высота может быть как положительной, так и отрицательной величиной.

9. Картезианские координаты часто также называют декартовыми независимо от того, к какому количеству измерений, двум или трем, термин применяется. Эти названия являются полными синонимами и отсылают к одному и тому же человеку — Рене Декарту (Des-Cartes). Однако здесь и в дальнейшем я буду использовать термин «картезианские» для обозначения трехмерных пространственных координат, а двумерные прямоугольные на плоскости, которые мы встретим в следующей части, буду называть «декартовыми». Просто для краткости, чтобы каждый раз не писать «система трехмерных прямоугольных координат» и было сразу понятно, о каком количестве измерений идет речь.

10. Мы здесь их расписывать не будем, они приведены в любом элементарном учебнике геодезии или математической картографии, например в этом: Л.М. Вахрамеева, Л.М. Бугаевский, З.Л. Казакова, «Математическая картография», 1986, М., «Недра», с.16. На этом этапе нам нужно лишь разобраться в их применении.

11. Координаты проекции являются двумерными прямоугольными, то есть «декартовыми» в принятой дальше терминологии (см. примеч. [9]).

12. Фактически, при расчете используют обычный в оптимизационных задачах метод наименьших квадратов.

13. Иногда встречается утверждение, что «WGS84» следует называть систему координат, которая основана на эллипсоиде GRS80. На мой взгляд, это совершенно неверно, GRS80 и WGS84 — это всего лишь две версии одного и того же эллипсоида, из самого названия понятно, что вторая версия более поздняя. Отличаются они лишь не значащими ничего для картографии последними знаками в величинах большой полуоси и сжатия. Тем не менее, тут снова есть неоднозначность: систему координат, основанную на втором эллипсоиде также называют «WGS84», однако в дальнейшем, во избежание путаницы, для системы координат мы будем придерживаться другого названия: «EPSG:4326». В этом примечании мы с вами забежали немного вперед, в следующую главу, но скоро станет совсем ясно, откуда берется такое название.

14. Пользуемся термином «географическая система координат», поскольку от геоида мы вернулись обратно на эллипсоид, а в этом случае, как мы с вами видели выше, географические и геодезические координаты совпадают.

15. При желании можно добавить еще и высоту точки над эллипсоидом, чтобы окончательно иметь трехмерную картину.

16. Вообще говоря, те «исторические» эллипсоиды, о которых шла речь выше, в том числе и эллипсоид Красовского, рассчитывались и предлагались первоначально как общеземные. Однако, по понятным причинам для их вычислений использовались в первую очередь данные, полученные на ограниченной территории, поэтому по факту они со временем стали референц-эллипсоидами. Только с развитием глобальных методов измерений появилась возможность расчета по-настоящему общеземного эллипсоида.

17. Кстати, на этом сайте есть множество материалов, очень доступно написанных, которые в этом цикле я не освещаю или, в целях упрощения, освещаю недостаточно подробно. Поэтому его можно было бы рекомендовать для первичного погружения в область математической картографии.

18. Я в дальнейшем буду использовать термин «7-параметрическое преобразование Гельмерта», поскольку, кажется, по нему встречается меньше всего разночтений. Но для понимания общей картины, а также умения разбираться в англоязычной литературе и и англоязычных же интерфейсах программ эти тонкости следовало бы знать.