Объединенные электронные атласы из многолистовых крупномасштабных карт XIX-XX веков. Теоретический минимум. Часть третья.

В предыдущей части мы с вами остановились на том, как определяются координаты и системы координат на трехмерных моделях Земли (в зависимости от требуемой точности представления и конкретных задач — на сфере, сфероиде и геоиде). Однако мы знаем, что карта — объект двумерный, плоский, и именно с такими объектами работают картографы [1] и именно такие объекты будут предметом нашего дальнейшего рассмотрения. Как же перейти от общего трехмерного представления реальной картины к изображению этого представления на плоскости?

На помощь приходят проекции. Понятие «проекция» так и определяется: как некий способ отображения трехмерной картины или отдельного трехмерного объекта на плоскость. Подробно такие способы отображения мы с вами рассмотрим немного позже, а сначала поговорим о том, как вообще можно отобразить координаты, заданные в трехмерном пространстве, на плоскость.

Первый способ такого отображения на самом деле мы с вами уже встречали в предыдущей части. Ведь все рисунки трехмерных объектов, например сферы или сфероида, были изображены на плоскости (экрана, или, если напечатать такой рисунок — на листе бумаги). При этом все линии, которые представляют значения равных широт (параллели) или долгот (меридианы), и которые на реальном трехмерном объекте (например, на сфере или сфероиде) являются окружностями или эллипсами, на наших изображениях выглядели некоторыми другими кривыми линиями. Именно так часто поступают при отображении этих линий и на реальных картах. В зависимости от способа отображения (то есть выбранной проекции) параллели и меридианы могут быть отображены прямыми линиями, окружностями или их дугами и в общем — совершенно произвольными кривыми, вид и форма которых задается только свойствами конкретной используемой проекции.

Есть и другой способ задать положение любой точки при изображении трехмерного объекта (всего или его части) на плоскости. Если мы нарисуем на ней плоскую систему прямоугольных координат (она еще называется декартовой [2]), то каждой точке изображения можно будет сопоставить значения абсциссы x и ординаты y в этой системе координат. Но тогда мы сможем сопоставить эти значения x и y и любой точке изображенным на плоскости в виде кривых параллели или меридиану, которые, в свою очередь представляют географические координаты на трехмерной модели. Оба способа проиллюстрированы на рисунке ниже, где синими линиями показаны линии параллелей и меридианов, проведенные с шагом в 1°, а красными — некоторая прямоугольная (декартова) система координат, смысл которой совсем скоро станет понятен.

Линии параллелей и меридианов, наложенные на декартову систему координат, выглядят как графики некоторых функций, которые можно записать в виде некоторых математических формул. Так оно и есть, и такие формулы называют формулами проекции [3], а проведенные линии (градусные или прямоугольные) называют сетками проекции.

О таких сетках следует также сказать несколько слов, поскольку и в этом случае имеется некоторая неоднозначность терминологии. В учебнике [4] градусная сетка, изображающая географические координаты, называется картографической, а декартова прямоугольная — координатной. Из таких названий не очень понятно, в чем заключаются их отличия, ведь в обоих случаях речь идет и о картографии, и о координатах. Но так довольно часто принято, поэтому в дальнейшем я так и буду их называть, не отказываясь, впрочем, от более простых понятий «градусная» и «декартова» [5].

Однако для того, чтобы декартова сетка стала системой координат, ей нужны еще три важных свойства. Нужно задать начало отсчета координат, их единицы и направление ее осей. Только тогда она станет однозначно связана с картографической сеткой, а следовательно, и с изображаемой на плоскости географической системой координат. И такие свойства для каждой проекции свои. Проще всего с единицами: для карт, близких к современности используют метры (именно они подписаны на рисунке выше у каждой вертикальной и горизонтальной красной линии). Для российских карт XIX века естественными единицами служили сажени и версты, мы с этим немного позже вплотную столкнемся. Что же касается начала отсчета и направления координатной сетки, то выбирают некоторые специальные направления и точки, которые для каждой проекции свои. Например, для конических и псевдоконических проекций (с их примерами мы тоже встретимся чуть позже) в качестве одного из направлений выбирают так называемый центральный меридиан проекции, а в качестве начала отсчета — пересечение этого центрального меридиана с еще одной характерной линией градусной (картографической) сетки — главной параллелью. И вот окончательно определенная таким образом система декартовых координат и называется системой координат проекции (или проецируемой системой координат, если пользоваться терминологией QGIS). Такие однозначно определяемые параметры, как долгота центрального меридиана, широта главной параллели и другие, а также единицы измерений называются параметрами проекции и учитываются в формулах проекции.

Стоит еще раз зафиксировать связь географической и проецируемой систем координат: как мы выяснили в предыдущей части, географическая система координат всегда определена на конкретном эллипсоиде или сфере, то есть на конкретном датуме. А координаты проекции однозначно связаны с географическими на плоскости через формулы проекции. Следовательно, и система координат проекции однозначно связана с географической системой координат (и только тогда имеет смысл, когда определена базовая для нее географическая система координат) [6].

Чтобы закончить разговор о сетках, уместно на минутку вернуться к Введению и вспомнить о том, что там я обсуждал еще такое не широко применяемое понятие, как «эквидистантная сетка» [7]. Мы им в дальнейшем будем довольно часто пользоваться, поэтому стоит тут немного добавить к сказанному во Введении. Фактически, эквидистантная сетка — это дополнительная координатная прямоугольная сетка, шаг которой совпадает с шагом размеров листов многолистовой карты, и изображенная вместе с сеткой, которая определена системой координат проекции. Как мы с вами помним из того обсуждения, В.Г. Щекотилов и сотр. всегда рассчитывает и изображает эту эквидистантную сетку «поверх» сетки, определенной проекцией Гаусса-Крюгера (и на этой проекции я немного подробнее тоже остановлюсь в следующей части). Собственно, и рассчитывается она в координатах, которые проекцией Гаусса-Крюгера определяются. Недостатки, связанные с использованием эквидистантной сетки в «чужой» для нее проекции я коротко во Введении уже обсудил, а дополнительно они будут раскрываться по ходу дальнейшего изложения [8]. Мы же с вами по большей части будем использовать эту эквидистантную сетку в той проекции, которая характерна именно для нее, и тогда, как мы увидим на практике, в целом она будет совпадать с сеткой, определяемой системой координат проекции (с учетом, конечно, возможного разного шага таких сеток).

Итак, мы с вами рассмотрели самые общие принципы и понятия, связанные с координатами и их системами, а также способы их отображения в зависимости от выбранной модели: сферы, сфероида, геоида или двумерной плоской картины. Однако прежде чем мы перейдем к более частным вопросам и примерам тех объектов, с которыми будем работать в дальнейшем, давайте сделаем еще две важных вещи.

Первое. Давайте еще раз по итогам последних двух частей сформулируем терминологию, которой будем в дальнейшем придерживаться.

• Географическими координатами мы будем называть координаты в угловых единицах, которые определены на сфере и сфероиде (эллипсоиде вращения);
• Геодезическими координатами называют как координаты в угловых единицах, определенные на геоиде, так и трехмерные линейные геоцентрические координаты. Этого названия мы постараемся по возможности избегать из-за такой неоднозначности [9], тем более, что в дальнейшем мы всегда будем использовать сферические и сфероидные модели, а для них достаточно понятия географических координат;
• Для описания прямоугольных геодезических координат в трехмерном пространстве мы будем использовать термин «картезианские координаты»;
• Географическую систему координат мы определим как систему, использующую географические координаты;
• При проецировании трехмерной фигуры Земли на плоскость географические координаты могут быть изображены в виде картографической сетки;
• В дополнение к картографической сетке используют координатную сетку, которая однозначно связана с картографической формулами проекции и определена через декартову систему координат или систему координат проекции.

Второе. Из предыдущего обсуждения мы с вами помним, что хотя для достаточно точного указания расположения растра по отношению к реальной местности достаточно указать всего несколько точек привязки или несколько параметров world-файла, которые однозначно свяжут «внутренние», пиксельные координаты растра с координатами на местности, сама величина этих «координат на местности» зависит от выбранной системы координат. Поэтому естественным образом можно сделать вывод о том, что эту систему координат нужно каким-то образом указывать для каждого растра. Так действительно и поступают. Проще всего это сделать с теми форматами, которые поддерживают метаданные, тогда используемую систему координат включают в метаданные. Внимательный читатель это уже видел в первой части, но все равно рисунок с метаданными стоит повторить и здесь. На нем мы видим, что система координат (в данном случае WGS84) указана в отдельном поле метаданных [10].

Как поступить, если растровый формат не позволяет хранить такие расширенные метаданные с геоинформацией? Или же можно задать такой вопрос: что делать, если мы создали свою, пользовательскую систему координат в одной программе, а теперь нам нужно перенести ее в другую? Очевидно, нужно поступить точно так же, как и в случае хранения точек привязки или world-файла: хранить данные о системе координат (как географической, так и системе координат конкретной проекции) в отдельном файле. Такой отдельный файл называется файлом проекции и обычно имеет расширение .prj [11]. Тут следует сразу сказать, что разновидностей таких описаний существует довольно много и сейчас мы с вами остановимся на некоторых из них. Заодно нам станут понятнее и нагляднее некоторые базовые концепции, которые мы с вами обсудили выше.

Ниже приведено содержимое двух файлов, хранящих информацию о проецируемой системе координат, записанные в часто применяемом формате «ESRI WKT». Хронологически, это один из самых первых стандартов, который применялся в программе ArcGIS и тем самым стал самым широко применяемым стандартом для обмена такими данными между различными программами [12]. Сразу обратим свое внимание на то, что непосредственно вслед за общим тегом, говорящим о том, что перед нами проецируемая система координат (PROJCS) и ее названием ("Bonne") идет описание базовой географической системы координат, на которой построена эта проецируемая система (GEOGCS). В свою очередь эта базовая система описана ее названием ("GCS_WGS_1984"), датумом (DATUM), начальным меридианом (PRIMEM), ее единицами, градусными в данном случае (UNIT), и параметрами использованного эллипсоида (SPHEROID). И лишь затем идет описание собственно проекции (PROJECTION), в данном случае проекции Бонна с ее параметрами (PARAMETER) и единицами (метрами).

Второе описание отличается от первого лишь тем, что в качестве сфероида использован так называемый «эллипсоид Вальбека», для которого также указываются его размеры, и названием этой географической системы координат.

Теперь посмотрим, что произойдет, если мы каким-нибудь способом поместим данные этих двух пользовательских систем координат в QGIS (как конкретно это сделать, мы узнаем, когда дело дойдет до практической работы). В QGIS эти текстовые описания будут выглядеть немного по-другому, но принцип построения описания останется тем же самым: вначале снова идет описание базовой географической системы координат (BASEGEOGCRS) вместе с описанием датума и сфероида, на котором этот датум основан, а затем — все остальное, касающееся собственно проекции. Это последняя, самая поздняя версия формата WKT, которую QGIS поддерживает через встроенные библиотеки GDAL и PROJ. Полностью этот формат записывают как OGC WKT2:2019 [13], указывая год выхода этого стандарта. Обилия видов таких форматов пугаться не стоит, QGIS прекрасно понимает все их разнообразие через те же библиотеки [14].

Обратим особое внимание, что у нас появились дополнительные строки вида «ID ["EPSG", xxxx]», где xxxx — какое-то число. С такими обозначениями в дальнейшем мы будем часто сталкиваться, поэтому здесь разберем, что они обозначают.

Каждое такое обозначение связано с уникальным объектом, который хранится в постоянно пополняемой и изменяемой базе данных, работой с ней в настоящее время занимается Комитет по геоматике (Geomatics Committee) Международной ассоциации производителей нефти и газа (IOGP) [15]. Как мы с вами видим, такие идентификаторы связаны не только с системами координат, но и с их элементами — датумами, эллипсоидами, параметрами проекций, методами расчета (то есть, формулами проекций), единицами измерений и т.д. К счастью, все эти обозначения нам запоминать не понадобится, подстановкой их в описание системы координат вполне интеллектуально занимается сама QGIS с помощью упомянутой выше библиотеки PROJ, которая является неотъемлемой частью этой ГИС. Полезно будет запомнить лишь обозначения нескольких систем координат, с которыми нам часто придется работать в дальнейшем и о которых пойдет речь в следующей главе. Здесь лишь хочу обратить внимание на то, что по сравнению с предыдущим разобранным нами вариантом формата ESRI WKT в описаниях систем координат добавился отдельный блок, который описывает систему координат проекции (CS[Cartesian,2]) и это буквально значит, что для такой системы используется двумерная прямоугольная система координат, которая здесь называется «картезианской», но мы с вами договорились называть ее «декартовой», чтобы отличать от трехмерной.

Формат WKT в настоящее время является самым современным, однако обязательно нужно сказать еще об одном формате, который считается устаревшим, но которым, пока он включен в современные дистрибутивы QGIS, полезно уметь пользоваться по ряду соображений, и мы это поймем в следующих частях цикла. Кроме того, на его примере сейчас будет понятно, откуда иногда возникает путаница с понятием «систем координат» и «проекций». Давайте посмотрим, как выглядит описание нашего второго примера с системой координат на «эллипсоиде Вальбека» в формате Proj4 и который в QGIS выводится сразу же после описания в WKT.

Мы с вами видим, что вначале фактически описывается проекция с ее параметрами, затем идет описание сфероида и лишь в конце указывается, что перед нами система координат. То есть, логика построения такой записи полностью «перевернута» по отношению к формату WKT.

К сожалению, именно такая логика используется до сих пор в популярной программе Global Mapper. Именно поэтому все настройки систем координат находятся в пункте меню «Projection». И даже географические системы координат в ней считаются «проекциями», что в корне расходится с принятыми в настоящее время стандартами. Можно даже сказать, что понятия «система координат» в Global Mapper нет вовсе, а есть лишь понятие «датум» и некоторая «географическая» («Geographic») проекция, определенная на конкретном датуме. Такой подход не очень мешает практической работе с картами, однако с точки зрения обобщения на другие системы координат (трехмерные географические, геодезические и т.д.) его нельзя признать удовлетворительным [16]. Так подробно я останавливаюсь на этом вопросе лишь потому, что этот разбор позволяет упорядочить логику современного подхода к изложению и то, как эта логика менялась со временем. Поэтому стоит повторить еще раз: проекция — это метод (использующий формулы и некоторые параметры), который мы применяем к географической системе координат, а результатом применения этого метода является система координат проекции.

В свете всего сказанного выше давайте посмотрим, как в QGIS выглядит описание географической системы координат, основанной на общеземном эллипсоиде WGS84. Ее код в системе EPSG записывается как EPSG:4326 и как я обещал в примечании в предыдущей части, так в дальнейшем мы и будем ее называть.

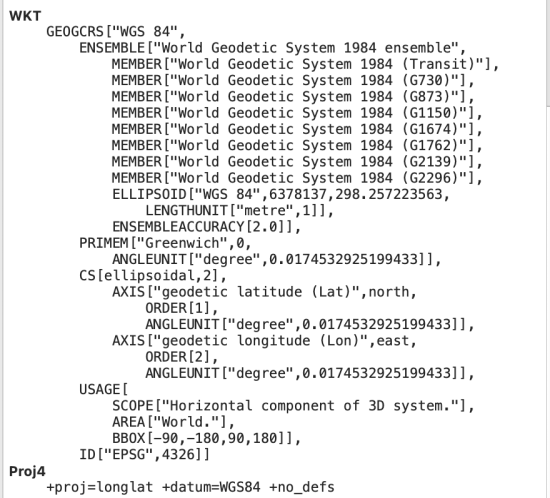
В описании в формате WKT мы в первую очередь видим, что система координат является географической (GEOGCRS). Из содержимого секции «CS» ясно, что, в отличие от проецируемых систем координат, примеры которых были приведены выше, координатная сетка является не декартовой, а определена на эллипсоиде (на его поверхности, об этом говорит запись «ellipsoidal,2» и измеряется в угловых единицах (градусах).

А вот описание в формате Proj4 вновь следует «перевернутой» логике: система координат в этом формате вновь называется «проекцией» (longlat) почти в точном соответствии с устаревшими обозначениями Global Mapper.

Но теперь мы с вами поняли их различия, не будем путать их и в дальнейшем. А в следующей части нас ждет обсуждение уже конкретных проецируемых систем координат и видов проекций, которые встретятся нам в дальнейшей работе.

Литература и примечания

1. Стоит сказать, что уже четверть века существуют так называемые программы-глобусы (Google Earth, ArcGIS Earth и другие), которые позволяют отображать карты на трехмерной поверхности (на самом деле, «псевдотрехмерной», поскольку конечное изображение получается на двумерном экране монитора и лишь имитирует трехмерность). Таким способом можно изобразить карту, не применяя те способы приведения трехмерной картины реального мира к двумерной, которые мы ниже рассматриваем. Однако пока что такие способы не то что не заменили двумерные изображения но даже не составили им серьезной конкуренции. Тем более это относится к принципиально двумерным электронным изображениям (сканам) исторических карт. В дальнейшем мы с вами все же будем изучать лишь классические, двумерные представления.

2. В предыдущей части мы уже узнали, что синоним декартовых координат — картезианские координаты. Но там же мы договорились употреблять название «картезианские» для прямоугольных трехмерных координат. А название «декартовы» давайте оставим для описываемых сейчас двумерных координат — снова лишь для краткости написания.

3. Строго говоря, этим визуальным образом мы определили так называемые обратные формулы проекции (зависимость широты или долготы от координат x и y). Прямые же формулы — это зависимость координат x или y на плоскости от широты и долготы. Однако здесь важен сам принцип такого определения. Как мне кажется, для общего понимания того, как образуется проекция, он гораздо более прост и нагляден, чем традиционное описание на одном или двух довольно частных примерах «наворачивания цилиндра на сферу» или «проецирования на плоскость околополярной области». Как я уже говорил, к этим частным примерам мы перейдем чуть позже.

4. Серапинас Б.Б. Математическая картография, М., Академия, 2005, с.25-27.

5. В англоязычной литературе и англоязычных интерфейсах программ для сеток употребляются два термина: «graticules» и «grids». Но и тут все немного запутано, иногда считают что первый термин обозначает картографические сетки, а второй — координатные, но так бывает далеко не всегда, и часто точный смысл можно понять только из контекста. Более того, термином «grid» называют и произвольный векторный объект, который может иметь свою собственную систему координат, не обязательно совпадающую с системой координатной сетки, и к тому же — не обязательно состоящий из линий, а например, из точек или шестиугольников. Чтобы окончательно не запутаться, оставим такие векторные объекты пока в стороне.

6. Впрочем, как всегда не бывает правил без исключений, и есть один вид проецируемых систем координат, где базовая географическая система координат не нужна и не используется. Это так называемые инженерные системы координат, подробнее мы с такими столкнемся в следующих главах.

7. Щекотилов В.Г. Метод оценки параметров эквидистантной системы листов крупномасштабной карты XIX в., Вестник ТвГУ, серия «География и геоэкология», 2010, вып. 1(8), № 33, с. 66.

8. Немного забегая вперед, можно сказать, что построения В.Г. Щекотилова и сотр. пренебрегают неизбежными искажениями, связанными с перепроецированием, в том числе — изменением длин и углов, и полагают эквидистантную сетку прямоугольной независимо от проекции, в которой она изображена.

9. Чего точно не следует делать — это называть прямоугольные декартовы координаты проекции «геодезическими», чем иногда грешат.

10. То же относится и к векторным форматам, где как вы помните, указываются координаты каждой точки, из которых состоят векторные объекты. В случае текстовых форматов система координат записывается в самом начале такого файла.

11. В этом названии сразу видна некоторая неоднозначность и путаница, которая часто выливается в недопонимание отличия системы координат (географической или проекции) от понятия самой проекции. На самом деле, файл содержит именно описание системы координат (может быть, географической, а может быть — и системы координат проекции). С такой неоднозначностью мы еще раз столкнемся немного позже.

12. WKT значит «well-known text» и является специальным образом отформатированным текстом (обратите внимание на квадратные скобки), который широко применяется не только для описания систем координат, но и для многих других целей, где нужно хранить данные в виде «название параметра – его значение».

13. OGC — Open Geospatial Consortium, организация, которая и занимается стандартизацией такого типа данных.

14. GDAL — библиотека с открытым кодом, предназначенная для работы специально с растровыми и векторными файлами. PROJ — такая же открытая библиотека для работы с системами координат и проекциями. В дальнейшем мы с ними еще не раз столкнемся.

15. EPSG — European Petroleum Survey Group была поглощена IOGP, однако историческое название для базы данных сохранилось. Подробно посмотреть эти данные или скачать их можно на сайте самого Комитета по геоматике, а также некоторых других (https://epsg.io/, https://spatialreference.org/ref/epsg/)

16. Впрочем, пока мы не выходим за пределы двумерных карт определенная логика в этом есть: чтобы изобразить географическую систему координат на двумерной плоскости приходится придумывать некоторую фиктивную проекцию, которая и называется «географической» (Geographic Lat/Lon в Global Mapper). Большого практического значения для изображения конкретных карт эта псевдопроекция не имеет, поскольку имеет большие искажения.