Объединенные электронные атласы из многолистовых крупномасштабных карт XIX-XX веков. Теоретический минимум. Часть четвертая.

В предыдущей главе мы с вами подробно разобрали такое понятие, как проецируемая система координат, но рассмотрение самих проекций отложили, ограничившись лишь коротким замечанием о том, что проекция в картографии — это метод отображения сферической или сфероидальной поверхности на плоскость. Теперь пришло время поговорить и о самих этих методах. А начнем мы с объяснения их разнообразия — такого, что только лишь для математической стороны вопроса существует целая научная дисциплина — математическая картография.

Не будет большим преувеличением сказать, что в основе как этого многообразия проекций, так и методов их изучения, лежит одно фундаментальное свойство: невозможность отображения сферы (или сфероида) на плоскость без тех или иных искажений [1]. Какие виды искажений бывают, и как они проявляются в различных проекциях мы скоро узнаем, а сейчас я считаю уместным сказать несколько слов о причинах невозможности отображения без искажений, тем более, что понимание таких причин напрямую связано с пониманием способов отображения сферы на плоскость (и соответствующей минимизацией тех или иных искажений). Она напрямую связана с фундаментальным свойством любой поверхности: ее кривизной. Под кривизной поверхности понимают вот что: если мы отметим на поверхности какую-нибудь точку, построим в этой точке нормаль [2] к поверхности и через эту нормаль проведем пересекающую поверхность плоскость, то линия пересечения поверхности плоскостью в этой точке также будет иметь некоторую кривизну. В свою очередь, кривизна линии определяется довольно просто: как величина, обратная радиусу «соприкасающейся окружности» [3] в этой точке. Понятно, что в общем виде кривизна линии будет зависеть от направления на поверхности (от того, как мы ориентировали пересекающую плоскость). Оказывается, что в любой точке поверхности существует максимальное и минимальное значение такой кривизны, причем по направлениям, взаимно перпендикулярным. Эти направления называются главными, а произведение кривизн по этим направлениям называют гауссовой кривизной поверхности в выбранной точке. Так вот, показано, что без искажений возможно отобразить одну на другую лишь поверхности с равной гауссовой кривизной. А поскольку гауссовы кривизны плоскости и сферы (сфероида) различаются, то согласно так называемой «замечательной теореме» (Theorema Egregium) Гаусса, без искажений такое отображение сделать нельзя [4].

Какие же виды искажений обычно рассматривают картографы? Ответ на этот вопрос как раз и объясняет многообразие проекций, ведь каждая проекция, как мы скоро увидим, решает определенные задачи, связанные с минимизацией лишь определенного круга искажений. Первые, и самые главные — это искажения длин. Как раз искажения длин (расстояний вдоль поверхности) при отображении сферической (сфероидальной) поверхности на плоскость являются первым следствием упомянутой в предыдущем абзаце теоремы и ответственны за растяжения и сжатия отображаемой поверхности. Основное, что нужно всегда помнить: не бывает такого отображения (проекции), которое бы сохраняло длины в любой точке отображаемой фигуры или территории. Такое сохранение возможно лишь только для отдельных направлений на поверхности и эти направления (и даже само их существование) как раз и определяются выбором той или иной проекции.

Площади и углы фигур при отображении (проецировании) в общем виде также искажаются, но в то же время существуют способы сохранения величин площадей или углов по всей поверхности. И здесь надо помнить еще одну важную вещь: невозможно одновременно сохранить величины и площадей, и углов. Можно сохранить только что-то одно или использовать какие-то промежуточные, компромиссные варианты [5].

Посложнее ситуация с сохранением форм. В общем виде формы объектов, особенно достаточно протяженных, не сохраняются, поскольку для такого сохранения нужно не только сохранение всех углов, но и площади любого участка объекта (а значит, и всей площади). Однако здесь есть предельное исключение: достаточно малые объекты могут сохранять формы с хорошей точностью (например, когда проекция сохраняет величины углов точно, а размер объекта достаточно мал, чтобы изменение площадей различных участков объекта можно было бы считать примерно постоянным). Такие проекции называют конформными и мы их скоро встретим, когда будем рассматривать некоторые примеры более подробно.

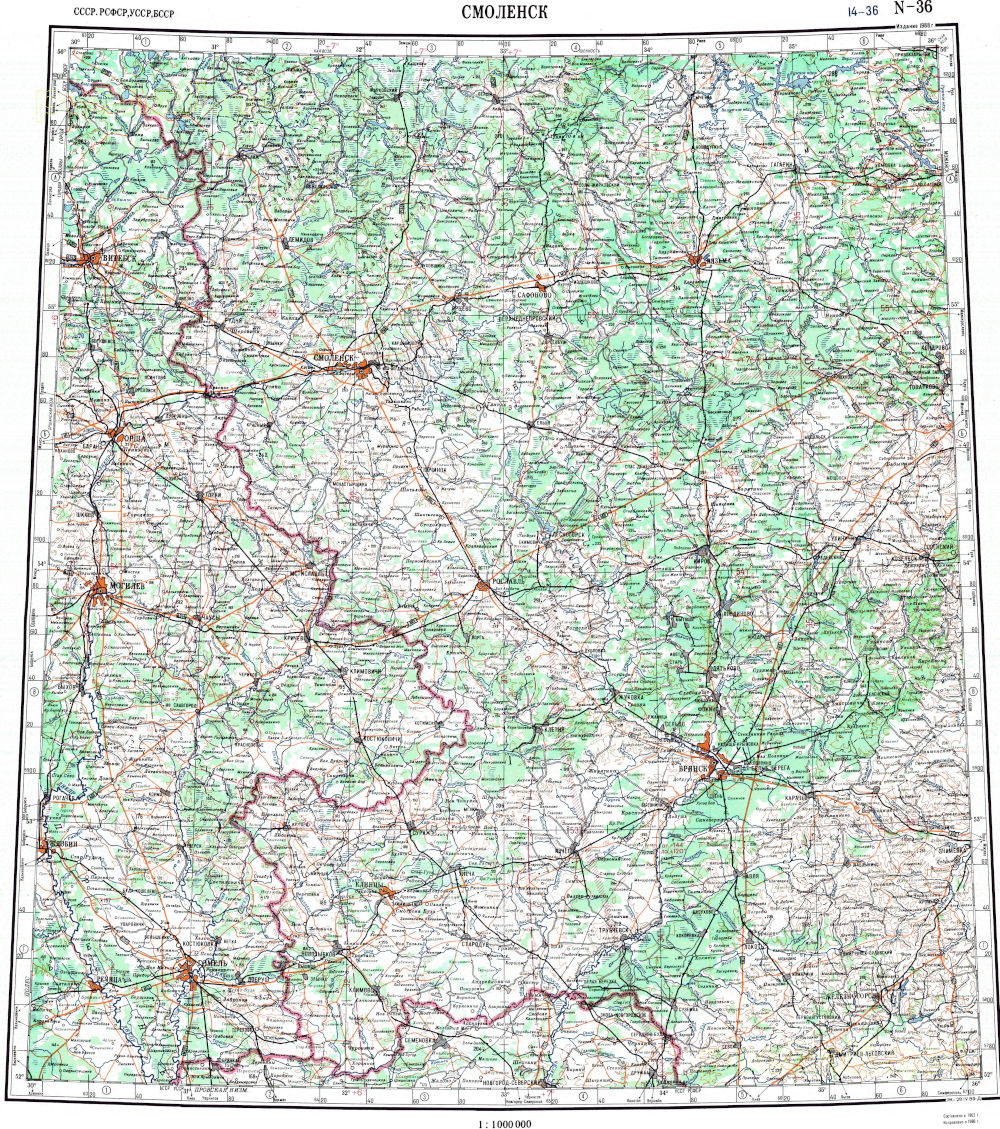
Чтобы окончательно понимать, о чем в дальнейшем пойдет речь, всегда полезно иметь перед глазами некоторый визуальный пример. В качестве такого примера дальше в этой и следующих двух главах мы с вами будем рассматривать участок местности (земного сфероида), ограниченного по широте параллелями в 52° и 56° с.ш., а по долготе — меридианами в 30° и 36°. Тем, кто когда-нибудь сталкивался с топографическими картами XX века, такое ограничение хорошо знакомо: оно обозначает один из листов «миллионной» (то есть масштаба «в одном сантиметре 10 км») карты, а именно карты номенклатуры N-36, которая и приведена на рисунке ниже. Почему мы будем рассматривать среднемасштабную а не крупномасштабную карту? Ответ прост: чем мельче масштаб карты, тем нагляднее проявятся те эффекты проекций, о которых в дальнейшем пойдет речь.

На самом деле, наш участок местности на рисунке выше уже изображен на плоскости и уже представляет собой карту, а следовательно, изображен в какой-то проекции [6]. Но на деталях этой проекции мы сейчас останавливаться не будем, а вместо этого попробуем представить, как этот участок выглядит в исходном трехмерном отображении.

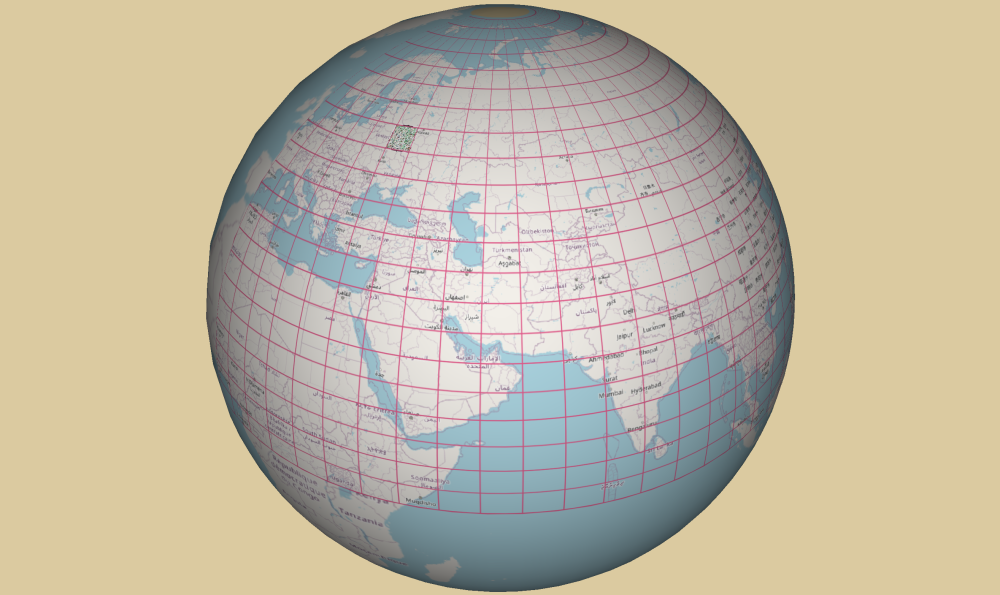
С недавних пор в QGIS существует свой встроенный «глобус» для трехмерного изображения карт, им мы и воспользуемся. Добавим на него для наглядности карту-подложку OSM, а также географическую (картографическую, градусную) сетку. Шаг сетки выберем равным границам исследуемого участка, то есть, параллели проведем через 4°, а меридианы — через 6°. Для дальнейшей наглядности отображения вида проекций ограничим сетку по долготе меридианами 0° и 180°, а по долготе — параллелями 0° и 84°, то есть возьмем восточную половину северного полушария. Вид получившегося глобуса вместе с исследуемым участком изображен на рисунке ниже.

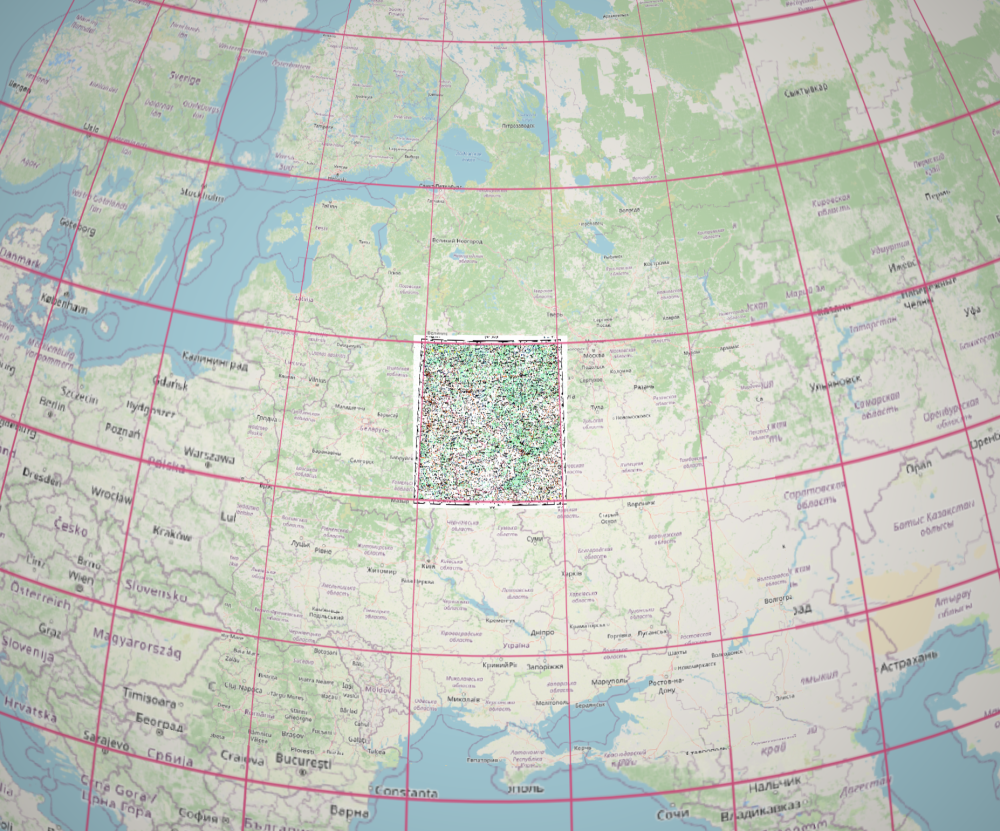
Теперь приблизимся к нашему участку и «посмотрим» на него строго сверху: прямо по центру участка. Видно, что он представляет собой криволинейную (сфероидическую) трапецию. С севера и юга она ограничена дугами окружностей параллелей, а с запада и востока — дугами окружностей (говоря точнее, эллипсов) меридианов. Очевидно также, что внутри одного пояса, ограниченного двумя линиями параллелей, все такие трапеции совершенно одинаковы по своим размерам и форме, а в меридиональном направлении — уменьшаются по ширине с юга на север, но при этом почти сохраняют свою высоту [7]. Кстати, карта, которую я привел с самого начала, выглядит очень похоже. Это потому, что она составлена в такой проекции, в которой для участка местности этих размеров искажения минимальны, а с учетом того, что она еще и уменьшена относительно своего реального масштаба, искажениями можно вообще пренебречь.

А теперь давайте проведем эксперимент и посмотрим на нашу криволинейную трапецию с разных ракурсов. На двух рисунках ниже приведен результат такого эксперимента. Видно, что в зависимости от положения точки зрения видимое изображение может менять как размер сторон, так и размер углов или собственную площадь. Это произошло потому, что на самом деле мы видим не реальную трехмерную картину, а картину, спроецированную на двумерную поверхность рисунка или экрана. Иллюзия «трехмерности» достигается вспомогательными способами: наложением теней на изображение, знанием о том, что поверхность нашего глобуса сферическая или сфероидальная и т.п. [8].

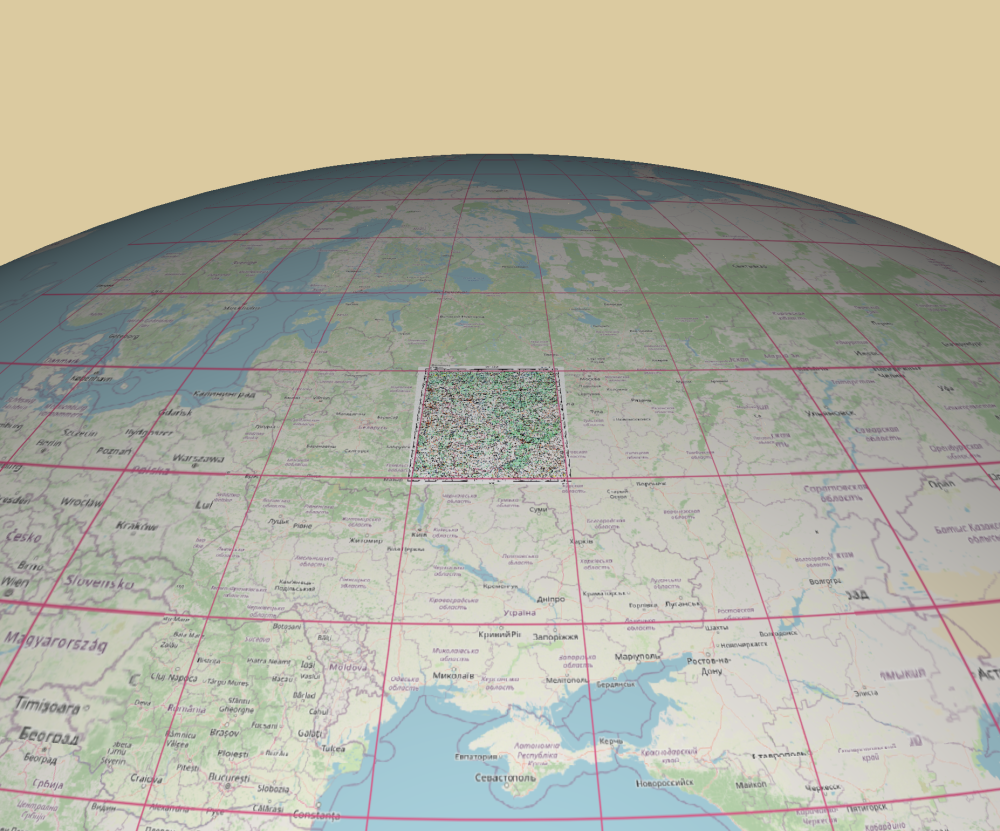
Стоит также обратить внимание на то, что вместе с формой объекта на последних двух рисунках меняется и форма самой картографической сетки.

Таким простым визуальным способом мы продемонстрировали самую суть проекций и тех эффектов, которые с ними связаны. Но теперь нам нужно как-то разобраться с чуть ли не бесконечным количеством проекций, которые были придуманы вплоть до настоящего времени.

Сразу же успокою читателя: мы не будем исследовать все возможные проекции, не будем даже рассматривать большинство из самых распространенных. Для этого существует множество литературы, которую можно порекомендовать для углубленного изучения, например справочники [9,10], очень доступно написанную книгу [11], а также любой учебник по математической картографии [12-14]. Не будет здесь и математической стороны, то есть формул проекций, их также легко найти в упомянутых книгах. В этой и следующих главах мы с вами остановимся лишь на тех проекциях, которые имеют какое-то отношение к исследуемому нами предмету: старым картам и современным методам их отображения. Правда, нам все же придется сказать несколько слов о классификации проекций, но больше для того, чтобы приобрести некоторые минимальные сведения, которые нам помогут в дальнейшем использовании и знании свойств той или иной проекции, а также позволит уверенно понимать некоторые специфические для этой темы термины (и здесь мы не можем обойтись без знания терминологии!) и осознавать границы применимости рассматриваемых проекций.

Самый простой способ классифицировать проекции напрашивается сразу же из рассмотрения трехмерного примера выше: разделить проекции по тому способу, с помощью которого мы смотрим на плоскость с нашей проекцией. Например, мы можем смотреть из центра сферы или сфероида на касающуюся этой сферы или сфероида плоскость, проецируя изображение вдоль лучей зрения (такие проекции называются гномоническими или центральными). Можно смотреть на ту же плоскость из точки, которая расположена на противоположной стороне сферы (и тогда мы получим стереографическую проекцию). А можно смотреть совсем «издалека», так, чтобы расхождением лучей зрения можно было бы пренебречь и считать их параллельными, примерно как на самом первом рисунке с общим видом глобуса (и тогда речь пойдет об ортографической проекции). Все это разнообразие способов объединяется в один большой класс перспективных проекций.

Но можно пойти и дальше. В самом начале главы мы с вами уже коснулись понятия искажений и поняли, что проекций без тех или иных искажений попросту не существует. Тогда напрашивается еще один способ классификации: по виду таких искажений. И тогда проекции можно разделить на равновеликие, которые сохраняют площадь объектов, равноугольные (они же называются «конформными», которые полностью сохраняют углы и хорошо — малые формы) и равнопромежуточные, которые сохраняют длины по какому-то выбранному направлению, называемому главным (эти направления мы обсудим, когда будем разбирать конкретные примеры проекций), но искажают и углы, и площади. Кроме того, существует и огромный класс так называемых произвольных проекций, которые искажают все — и площади, и углы, и расстояния (длины), но определенным компромиссным образом, подобранным под решение конкретной задачи.

Наконец, есть еще один важный способ построения проекций, которого мы пока не касались, ограничиваясь обсуждением способов проецирования сферы или сфероида сразу на плоскость, но с которым мы с вами еще не раз столкнемся и который определяет еще одну классификацию проекций. Этот способ использует некоторую промежуточную поверхность, на которую вначале проецируется исходная поверхность сферы (сфероида), а уже потом эта промежуточная (вспомогательная) поверхность проецируется на плоскость. Такой способ имеет самое непосредственное отношение к кривизнам, которые мы обсуждали в самом начале главы и его стоит рассмотреть немного подробнее, тем более, что это поможет нам лучше понять свойства конкретных проекций. Кроме того, этот способ лежит в основе более общей классификации проекций: по форме их картографической сетки. Примеры такой классификации мы увидим, когда будем обсуждать те проекции, которые нам понадобятся в дальнейшем, там же и обсудим эти формы, сейчас же имеет смысл лишь перечислить самые основные: цилиндрические и псевдоцилиндрические, конические, поликонические и псевдоконические, азимутальные, круговые и т.д.

Сама идея способа заключается вот в чем. Если мы проецируем поверхность сферы (сфероида) сразу на плоскость, то наименьших искажений следует ожидать лишь в одной, очень небольшой области: там, где плоскость непосредственно примыкает к сфере или сфероиду. Это область вокруг так называемой центральной точки [15]. Чем дальше мы удаляемся от этой области, тем дальше располагается плоскость проекции от сферы и просто математически можно показать, что искажения будут нарастать все больше и больше. В то же время, «обернув» сферу или сфероид некоторой подходящей поверхностью, можно ожидать, что область минимальных искажений расширится — на всем протяжении нашего «направления оборачивания». Поясню наглядным примером: мы можем проецировать поверхность сферы [16] на плоскость, касающуюся сферы в какой-то выбранной точке экватора, и тогда минимальные искажения будут лишь в небольшой области вокруг этой точки, а при удалении от нее в любом направлении будут нарастать. Если же «обернуть» сферу цилиндрической поверхностью, то эта поверхность будет «хорошо прилегать» к поверхности сферы на всем протяжении линии экватора, и тогда по крайней мере в некоторой области вдоль всей этой линии искажения будут минимальны. В данном случае речь идет уже о некоторой центральной линии проекции [17]. А дальше происходит буквальная магия: если мы теперь развернем цилиндр в плоскость, то дальнейших искажений уже не получим! Мы это обсудили в самом начале главы — цилиндрическая поверхность имеет нулевую гауссову кривизну и следовательно может быть отображена на плоскость (также поверхность с нулевой гауссовой кривизной) без искажений.

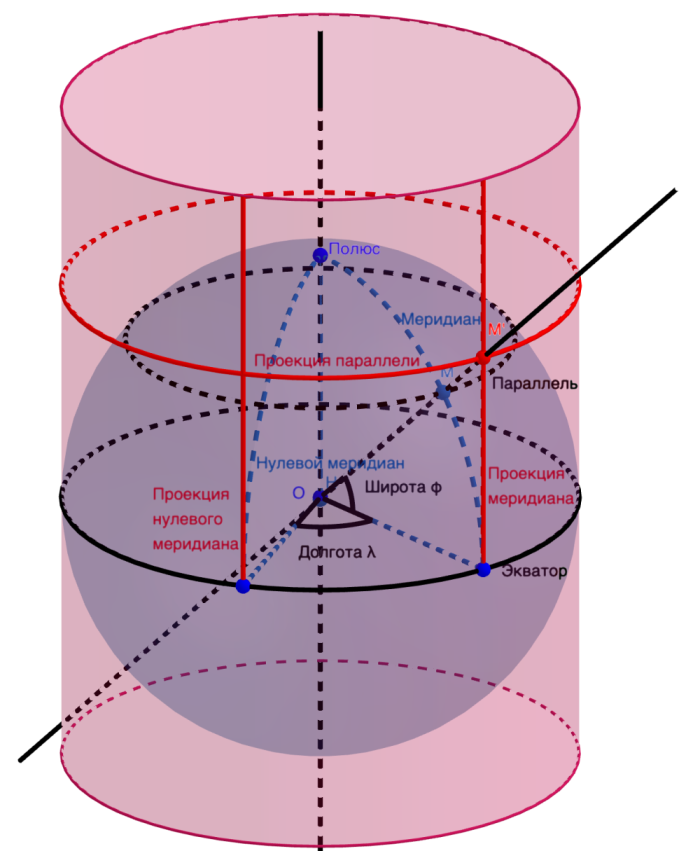
Тот способ, который мы только что описали, и который схематично изображен на рисунке выше, определяет класс цилиндрических проекций. В зависимости от расположения такой цилиндрической поверхности можно построить дальнейшее разделение: на прямые или нормальные проекции (когда цилиндр оборачивает сферу по экватору так же, как на рисунке) и поперечные (когда цилиндр оборачивает сферу по какому-то выбранному меридиану). В первом случае искажения будут минимальны в области вдоль всей линии экватора (и полностью отсутствовать на самой линии), а во втором — вдоль всей линии этого выбранного меридиана.

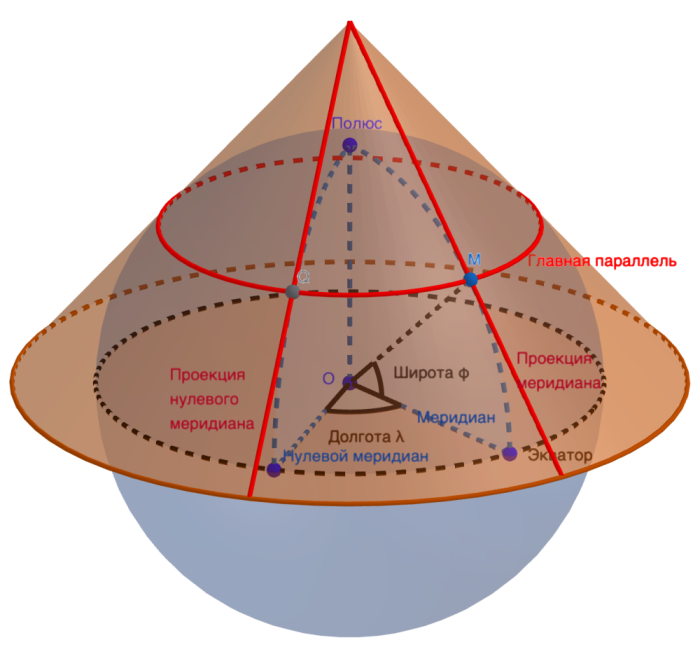
Есть и еще одна «волшебная» поверхность, которую можно развернуть в плоскость без искажений, и которую часто используют. Это конус, и такие построения определяют класс конических проекций. В данном случае «оборачивание» сферы производится вдоль какой-то выбранной параллели, называемой «главной» и в области вдоль всей этой параллели и следует ожидать минимальных искажений. На рисунке ниже приведен такой способ построения конической поверхности.

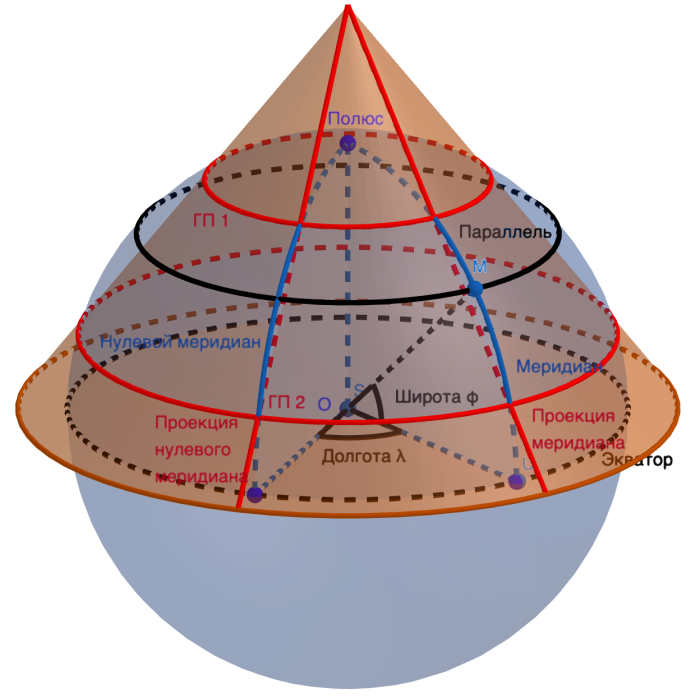
В цилиндрических и конических проекциях широко используют один прием расширения области минимальных искажений, с которым при описании конкретных проекций мы обязательно столкнемся. Цилиндр или конус не обязательно оборачивать вокруг сферы так, чтобы он ее касался по одной линии. Можно «погрузить» эту вспомогательную поверхность под поверхность сферы и тогда она будет пересекать сферу уже по двум линиям (в случае конических проекций это две параллели, и обе они называются главными), на которых искажения будут отсутствовать, а в обе стороны от них искажения будут менять знак, проходя через ноль. Следовательно, можно ожидать, что область малых искажений займет более широкую полосу, что схематично показано на следующем рисунке.

Азимутальные проекции в дальнейшем нам не встретятся, поэтому их особенности я упомяну лишь для ознакомления. Во-первых, промежуточная поверхность, отличная от плоскости, в них не используется, а во-вторых, обычно в них используют свою специальную координатную сетку не в декартовых, а в полярных координатах. Правда, здесь уместно заметить, что в систематических курсах математической картографии рассмотрение всех трех видов (цилиндрические, конические и азимутальные) начинают с наиболее общего рассмотрения конических проекций, из которых оставшиеся получаются как предельный переход при движении к северу или югу параллели касания конусом сферы или сфероида. Если линия касания стягивается в точку к полюсу, то получаем азимутальную проекцию, если же двигаться наоборот, к экватору, то при его достижении вершина конуса уйдет на бесконечность и мы получим цилиндрическую поверхность и проекцию.

Наконец, для понимания того, что классификация по виду промежуточной поверхности является лишь частным случаем более общей классификации — по виду сетки, назовем еще один вид проекций — аналитические или условные. Это проекции, для которых невозможна простая геометрическая интерпретация с промежуточной поверхностью, такая, как в случае цилиндрических или конических проекций, и которые можно описать лишь в виде формул проекции (Помните пример сеток из предыдущей части, где мы даже не обсуждали геометрическую интерпретацию проецирования? Это и есть наиболее общий способ определения проекции). Очень часто такие проекции сохраняют определенные свойства проекций, использующих промежуточную поверхность, например, форму параллелей в виде прямых или окружностей, и тогда в их название добавляют «псевдо-», например, говорят о псевдоконической или псевдоцилиндрической. Пример такой проекции мы также увидим далее. Бывает и так, что промежуточная поверхность геометрически представима, но непредставим наглядно «закон перспективы» — так, как это делается в случае перспективных проекций. И эти виды проекций тоже надо считать аналитическими, и мы тоже скоро узнаем об одной такой (очень распространенной) проекции.

Однако наш рассказ о способах классификации проекций будет неполон без хотя бы краткого упоминания так называемых многогранных проекций. Во-первых, такие проекции довольно часто использовались в прошлом при составлении многолистовых карт, а также для съемки местности, а во-вторых, здесь еще раз проявится та неоднозначность в терминологии между «проекцией» и «системой координат», которую мы с вами разбирали в предыдущей части. Коротко и упрощенно принцип построения таких проекций можно изложить так: для участка местности на сфере или сфероиде, ограниченного какими-то выбранными линиями географической сетки (сферической или сфероидической трапеции) находится центральная точка, к которой проводится касательная плоскость. Если участок местности относительно невелик, то эту сфероидическую трапецию можно спроецировать на плоскость линиями, перпендикулярными плоскости, уже на плоскую трапецию (при этом можно пренебречь искажением первоначальной кривизны линий, изобразив их в виде прямых). Такую процедуру повторяют для всех участков сетки. При этом у нас получится многогранник, описанный вокруг первоначальной сферы [18]. Здесь нетрудно видеть, что основным недостатком таких построений является невозможность «склейки» обширных площадей в единое изображение без разрывов. На рисунке ниже показаны такие разрывы, которые обязательно появляются при разворачивании многогранника на плоскость.

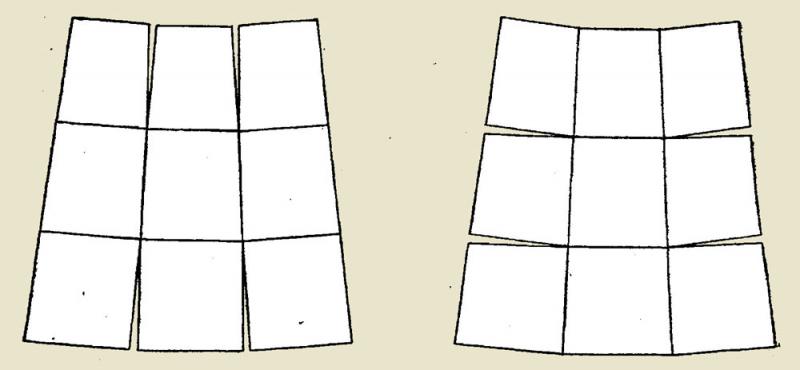
Поэтому такие «проекции» не применяются для изображения обширных площадей, а используются в их исходном «многолистовом» варианте. На примерах таких «проекций» мы остановимся в следующей части, а здесь же я хочу пояснить, почему уже несколько раз взял слово «проекции» в кавычки.

Как мы с вами помним из предыдущей части, современное описание проецируемой системы координат включает в себя базовую географическую систему координат и описание проекции как метода, но с обязательным указанием ее параметров. Но использование каждый раз для каждого участка своей центральной точки подразумевает изменение и указание каждый раз и параметров проекции. А следовательно, каждый раз речь идет о своей отдельной проецируемой системе координат. Или выражаясь другими словами, когда мы говорим о «многогранных проекциях», на самом деле каждый раз мы подразумеваем «многогранные проецируемые системы координат», или говоря еще точнее — наборы таких систем [19].

Именно поэтому в следующих двух частях, когда мы поведем речь о подробном описании уже конкретных проекций, мы будем рассматривать их (по возможности, конечно) как проецируемые системы координат: с указанием базовой географической системы и параметров этих проекций. Именно к такой конкретике подталкивает практическое применение современного инструментария геоинформационных систем.

Литература и примечания

Под «искажениями» здесь понимаются растяжения, сжатия, разрывы, перехлесты и т.д. Простые изгибы поверхности (такие, как например, сворачивание плоской поверхности в цилиндр или конус), сохраняющие расстояния вдоль поверхности, искажениями не считаются.
Определение нормали к поверхности см. во второй части части «теоретического минимума».
Соприкасающаяся окружность — аналог касательной прямой и определяется похожим образом. Можно назвать ее «наилучшим образом касающейся окружностью».
Гауссова кривизна плоскости в любой точке равна нулю, так как бесконечен радиус любой соприкасающейся окружности. Гауссова кривизна сферы равна 1/R², где R — радиус сферы, поскольку в любой точке сферы соприкасающаяся окружность — это попросту окружность радиуса R. Для сфероида (эллипсоида вращения) гауссова кривизна — переменная величина, зависящая от широты, но очевидно всегда больше нуля. Очень важным и замечательным является тот факт, что нулевой является и гауссова кривизна цилиндрической и конической поверхностей, поскольку на них всегда есть направление с нулевой кривизной (образующие цилиндра или конуса). Следовательно, цилиндрическую или коническую поверхность всегда можно отобразить на плоскость без искажений.
Если бы было возможно такое одновременное сохранение, то при сохранении величин углов любой прямоугольный треугольник преобразовывался бы в ему подобный. А при сохранении величин площадей и стороны его стали бы равны исходному, но тогда для произвольного прямоугольного треугольника всегда сохранялись бы длины сторон, что запрещает теорема Гаусса.
Для любителей снова немного забежать вперед: карта представляет собой пример проекции, которая называется проекцией Гаусса-Крюгера, представляет собой одну из самых распространенных разновидностей поперечных цилиндрических проекций, и подробно мы ее обязательно скоро рассмотрим. Не следует путать эту карту, которую в обиходе часто называют «миллионкой», с Международной (миллионной) картой мира, IMW, составленной в поликонической проекции.
«Почти» — потому, что для сфероида длины дуг между равноотстоящими параллелями немного не равны друг другу, в отличие от сферы, для которой эти длины дуг совершенно одинаковы. Впрочем, мы сейчас рассматриваем такие мелкие масштабы, что таким неравенством можно совершенно пренебречь.
Можно даже задаться вопросом: в состоянии ли мы вообще увидеть реальную трехмерную картину, даже если мы будем рассматривать реальный трехмерный глобус, ведь на самом деле изображение формируется на двумерной сетчатке глаза и лишь бинокулярность нашего зрения позволяет оценить «трехмерность»? Однако рассуждения на эту тему уведут нас слишком далеко от обсуждаемых вопросов.
Map Projections-A Working Manual. U.S. Geological Survey, Washington, 1987.
Geomatics Guidance Note Number 7, part 2, Coordinate Conversions and Transformations including Formulas, IOGP Publication 373-7-2, September 2019.
Лебедева О.А. Картографические проекции. Методическое пособие, Новосибирск, 2000.
Серапинас Б.Б. Математическая картография, 2005 М., Академия.
Л.М. Вахрамеева, Л.М. Бугаевский, З.Л. Казакова, «Математическая картография», 1986, М., «Недра».
В.В. Каврайский. Математическая картография, 1934 М.-Л., СССР–НКТП–ГГГГУ.
Точное определение центральной точки — это точка, где искажения проекции проходят через экстремум, то есть максимум или минимум, см. [14], с. 52. В данном случае речь идет о минимуме.
Для краткости дальше я буду писать про сферу, подразумевая и сфероид тоже, для него все нижесказанное так же справедливо.
Центральная линия определяется сходным с центральной точкой образом: как линия, где искажения экстремальны (минимальны или максимальны), а в частности, могут быть и равны нулю [14], с. 53.
Можно так же строить и вписанный многогранник, если будем строить плоскости, опирающиеся не на центральную точку, а на углы первоначальной криволинейной трапеции. Суть дальнейших рассуждений от этого не меняется, только разрывы заменятся нахлестами.
Неоднозначности терминологии, с которыми приходится сталкиваться при обсуждении многогранных проекций, много шире изложенных в основном тексте. Многое зависит от того, насколько авторы обобщают способы построения таких проекций. Мы рассмотрели самый простой способ: с касающейся или секущей плоскостью для каждого участка такой проекции, при этом еще и пренебрегли кривизнами линий на плоскости проекции. Можно такой кривизной и не пренебрегать, мы коротко остановимся на этом в следующей части, когда посмотрим на Международную миллионную карту подробнее. Но тогда такие дальнейшие обобщения могут привести к тому, что и проекцию Гаусса-Крюгера следует называть многогранной, как впрочем, это иногда и делают, ведь она тоже изображается с разрывами. Все же мне представляется, что многогранными (проекциями, или говоря точнее, проецируемыми системами координат), следует называть более простые варианты проекций, наподобие примера, изложенного в основном тексте.